数据结构学习笔记（三） 树形结构之利用堆构造哈夫曼树

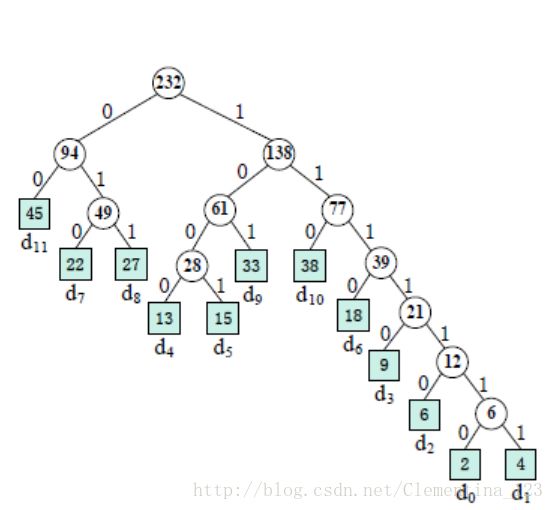
以下是利用堆构造huffman树的示例，最终构造结果如下图所示：

#include
using namespace std;

//抽象数据类型
const int m=12;  //外部结点的数目
typedef char datatype;
typedef struct node1
{
    float key;//权值
    datatype data;
    struct node1 *lchild,*rchild;
}HTnode;//哈夫曼树结点
const int DefaultSize=20;
typedef struct
{
    float key;//权值
    datatype data;
    HTnode *ptr;
}node;//堆结点
typedef struct
{
    node *Heap;
    int CurrentSize;
    int MaxHeapSize;
}minHeap;
minHeap mh;
node W[m];
int i,j,start,EndOfHeap;
node temp,item,first,second;
HTnode *root,*p;

//筛选法
void FilterDown(minHeap &mh,int start,int EndOfHeap)
{
    int i=start,j=2*i+1;
    node temp=mh.Heap[i];
    while(j<=EndOfHeap)
    {
        if(j.Heap[j].key>mh.Heap[j+1].key)
            j++;
        if(temp.key<=mh.Heap[j].key)
            break;
        else
        {
            mh.Heap[i]=mh.Heap[j];
            i=j;
            j=2*j+1;
        }
        mh.Heap[i]=temp;
    }
}

//建立最小堆
void MinHeap(minHeap &mh,node A[],int n)
{
    int i,CurrentPos;
    mh.MaxHeapSize=DefaultSize.Heap=new node[mh.MaxHeapSize];
    if(mh.Heap==NULL)
    {
        cout<<"Memory Allocation Error1"<return;
    }
    for(i=0;i.Heap[i]=A[i];
    mh.CurrentSize=n;
    CurrentPos=(mh.CurrentSize-2)/2;
    while(CurrentPos>=0)
    {
        FilterDown(mh,CurrentPos,mh.CurrentSize-1);
        CurrentPos--;
    }
}

//堆的删除
node Delete(minHeap &mh)
{
    if(mh.CurrentSize==0)
    {
        cout<<"Heap Empty!"<return {0};
    }
    node item=mh.Heap[0];
    mh.Heap[0]=mh.Heap[mh.CurrentSize-1];
    mh.CurrentSize--;
    FilterDown(mh,0,mh.CurrentSize-1);
    return item;
}

//从下向上调整
void FilterUp(minHeap &mh,int m)
{
    int j=m,i=(j-1)/2;
    node temp=mh.Heap[j];
    while(j>0)
    {
        if(mh.Heap[i].key<=temp.key)
            break;
        else
        {
            mh.Heap[j]=mh.Heap[i];
            j=i;
            i=(j-1)/2;
        }
    }
        mh.Heap[j]=temp;
}

//堆的插入
int Insert(minHeap &mh,node item)
{
    if(mh.CurrentSize==mh.MaxHeapSize)
    {
        cout<<"Heap Full!"<return 0;
    }
    mh.Heap[mh.CurrentSize]=item;
    FilterUp(mh,mh.CurrentSize);
    mh.CurrentSize++;
    return 1;
}

//利用最小堆构造huffman树
void MakeHuffmanTree(node W[],int m,HTnode* &root)
{
    minHeap mh;
    node item,first,second;
    HTnode *p;
    int i;
    for(i=0;i.ptr=p;
        p->key=W[i].key;
        p->data=W[i].data;
        p->lchild=p->rchild=NULL;
    }
    MinHeap(mh,W,m);
    for(i=1;ikey=first.key+second.key;
        p->lchild=first.ptr;
        p->rchild=second.ptr;
        item.key=p->key;
        item.ptr=p;
        Insert(mh,item);
    }
    first=Delete(mh);
    root=first.ptr;
}

//使用递归进行前序遍历输出
void preOrder(HTnode* root)
{
    HTnode *p=root;
    if(p!=NULL)
    {
        cout<key<<" ";
        preOrder(p->lchild);
        preOrder(p->rchild);
    }
}

//测试方法
int main()
{
    node W[12]={{45,'A',NULL},{22,'B',NULL},{27,'C',NULL},
                            {13,'D',NULL},{15,'E',NULL},{33,'F',NULL},
                            {38,'G',NULL},{18,'H',NULL},{9,'I',NULL},
                            {6,'J',NULL},{2,'K',NULL},{4,'L',NULL}};
    HTnode *root=new HTnode;
    MakeHuffmanTree(W,12,root);
    cout<<"使用前序遍历方法，打印构建的huffman树各结点的权值："<"(可参考图验证huffman树的构建结果)"<return 0;
}