【题解】洛谷 P1014 【Cantor表】
1. 我们先引入三角形数的概念:
_ >定数目的点或圆在等距离的排列下可以形成一个等边三角形,这样的数被称为三角形数。古希腊著名科学家毕达哥拉斯把数1,3,6,10,15,21……这些数量的(石子),都可以排成三角形,像这样的数称为三角形数。_
>>三角形数_百度百科
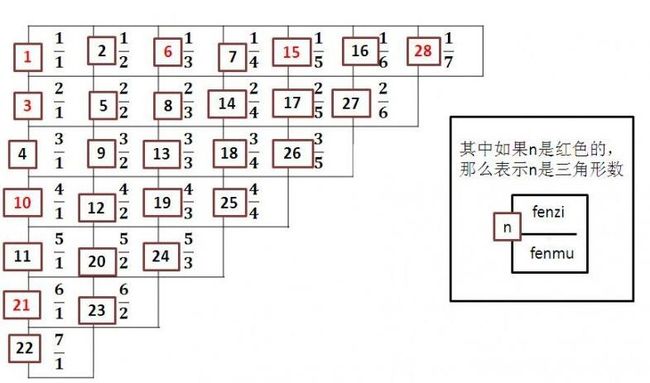
2. 我们来看看这个表:
3. 我们可以发现,设
x 1 < n ⩽ x 2 x_1 < n \leqslant x_2 x1<n⩽x2(其 x 1 x_1 x1、 x 2 x_2 x2均为三角形数)
即有 p ( p − 1 ) 2 < n ⩽ p ( p + 1 ) 2 \dfrac{p(p-1)}{2} < n \leqslant \dfrac{p(p+1)}{2} 2p(p−1)<n⩽2p(p+1),其中 p ∈ Z p \in Z p∈Z
也就是 { p 2 + p ⩾ 2 n … … ( 1 ) p 2 − p < 2 n … … ( 2 ) \begin{cases}p^2+p\geqslant2n……(1)\\p^2-p<2n……(2)\end{cases} {p2+p⩾2n……(1)p2−p<2n……(2)
对于(1),我们有 p 2 + p + 1 4 ⩾ 2 n + 1 4 p^2 + p + \dfrac{1}{4} \geqslant 2n + \dfrac{1}{4} p2+p+41⩾2n+41
配方得:
( p + 1 2 ) 2 ⩾ 2 n + 1 4 (p+\dfrac{1}{2})^2 \geqslant 2n+\dfrac{1}{4} (p+21)2⩾2n+41
∴ p + 1 2 ⩾ 2 n + 1 4 \therefore p+\dfrac{1}{2}\geqslant \sqrt{2n+\dfrac{1}{4}} ∴p+21⩾2n+41 或 p + 1 2 ⩽ − 2 n + 1 4 p+\dfrac{1}{2} \leqslant-\sqrt{2n+\dfrac{1}{4}} p+21⩽−2n+41
∴ p ⩾ 2 n + 1 4 − 1 2 \therefore p\geqslant \sqrt{2n+\dfrac{1}{4}}-\dfrac{1}{2} ∴p⩾2n+41−21 或 p ⩽ − 2 n + 1 4 − 1 2 p\leqslant-\sqrt{2n+\dfrac{1}{4}}-\dfrac{1}{2} p⩽−2n+41−21
对于(2),我们有 p 2 − p + 1 4 < 2 n + 1 4 p^2 - p + \dfrac{1}{4} < 2n + \dfrac{1}{4} p2−p+41<2n+41
配方得:
( p − 1 2 ) 2 < 2 n + 1 4 (p-\dfrac{1}{2})^2 < 2n+\dfrac{1}{4} (p−21)2<2n+41
∴ − 2 n + 1 4 < p − 1 2 < 2 n + 1 4 \therefore-\sqrt{2n+\dfrac{1}{4}}<p-\dfrac{1}{2}<\sqrt{2n+\dfrac{1}{4}} ∴−2n+41<p−21<2n+41
∴ − 2 n + 1 4 + 1 2 < p < 2 n + 1 4 + 1 2 \therefore-\sqrt{2n+\dfrac{1}{4}}+\dfrac{1}{2}<p<\sqrt{2n+\dfrac{1}{4}}+\dfrac{1}{2} ∴−2n+41+21<p<2n+41+21
为了方便,我们设 t = 2 n + 1 4 t=\sqrt{2n+\dfrac{1}{4}} t=2n+41
∴ \therefore ∴联立得: { p ⩾ t − 1 2 ∣ ∣ p ⩽ − t − 1 2 − t + 1 2 < p < t + 1 2 \begin{cases}p\geqslant t-\dfrac{1}{2} || p\leqslant- t - \dfrac{1}{2} \\-t+\dfrac{1}{2}<p<t+\dfrac{1}{2}\end{cases} ⎩⎪⎨⎪⎧p⩾t−21∣∣p⩽−t−21−t+21<p<t+21
解得: t − 1 2 ⩽ p < t + 1 2 t-\dfrac{1}{2}\leqslant p < t+ \dfrac{1}{2} t−21⩽p<t+21
又 ∵ t − 1 2 \because t- \dfrac{1}{2} ∵t−21到 t + 1 2 t+\dfrac{1}{2} t+21中只可能有1个整数
∴ p = ⌈ t − 1 2 ⌉ \therefore p= \lceil t- \dfrac{1}{2} \rceil ∴p=⌈t−21⌉
4. 我们再来找规律
我们再设 Δ s = x 2 − n \Delta s=x_2-n Δs=x2−n
所以
当p为偶数时:要求的结果 p − Δ s 1 + Δ s = p − x 2 + n 1 + x 2 − n \dfrac{p-\Delta s}{1+\Delta s}=\dfrac{p-x_2+n}{1+ x_2-n} 1+Δsp−Δs=1+x2−np−x2+n
化简后
分子是: p − p ( p + 1 ) 2 + n p-\dfrac{p(p+1)}{2}+n p−2p(p+1)+n
分母是: 1 + p ( p + 1 ) 2 − n 1+\dfrac{p(p+1)}{2}-n 1+2p(p+1)−n
当p为奇数时:要求的结果
1 + Δ s p − Δ s = 1 + x 2 − n p − x 2 + n \dfrac{1+\Delta s}{p-\Delta s}=\dfrac{1+ x_2-n}{p-x_2+n} p−Δs1+Δs=p−x2+n1+x2−n
化简后
分子是: 1 + p ( p + 1 ) 2 − n 1+\dfrac{p(p+1)}{2}-n 1+2p(p+1)−n
分母是: p − p ( p + 1 ) 2 + n p-\dfrac{p(p+1)}{2}+n p−2p(p+1)+n
所以我们就有了这个代码:
#include