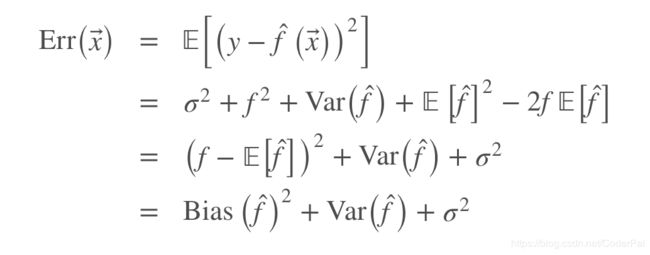（二）bagging 方法

作者：chen_h
微信号 & QQ：862251340
微信公众号：coderpai

---

在之前的文章中，你看到了不同的分类算法以及如何正确验证和评估模型质量的技术。现在，我假设你已经为你的问题选择了最佳模型，并且正在努力进一步提高其准确性。在这种情况下，你需要应用一些更高级的机器学习技术，其中有一种技术就是集成学习。

集成学习是由一组共同分类器或者不同分类器来作为一个整体。举个例子，比如一个音乐会，我们会同时演奏好几种不同的乐器，来构成美妙的音乐，这个合奏的过程就是集成学习，我们来收集不同的音符，从而组装成不同的美妙音乐。

1. 集成

法庭陪审团在某种意义上讲就是一个集成学习。它指出，如果陪审团的每个成员做出独立判断并且每个陪审员正确决定的概率大于 0.5 ，那么整个陪审团正确决定的概率随着陪审员总数的增加而增加，并且最终会倾向于 1。另一方面，如果每个陪审员的正确概率小于 0.5 ，那么整个陪审团正确决定的概率随着陪审员的数量增加而减少，并趋于零。

让我们为整个定理写一个简单的表达式：

• N 表示陪审员总数；
• m 表示占多数意见的最小陪审员数量，即 $m=\frac{N+1}{2}$；
• $\left(\genfrac{}{}{0ex}{}{N}{i}\right)$ 是具有 N 个元素的集合中的 i 个元素组合的数量；
• p 表示陪审员正确决定的概率；
• $\mu$ 表示整个陪审团正确决定的概率；

那么：

$\mu = \sum^{{N}_{i=m}\binom{N}{i}p}{i}(1-p)^{N-i} $

从等式中，我们可以看到，如果 $p>0.5$ ，那么 $\mu >p$ 。而且，如果 $N\to \infty$ ，那么 $\mu \to 1$ 。

让我们看另一个非常有名的集成学习例子：在 1906 年，Francis Galton 参观了普利茅斯的一个乡村集市，在哪里他看到了为农民举办的比赛。800 名参与者试图估计被屠宰的公牛的重量。公牛的实际重量是 1198 磅。虽然没有一个农民可以猜出动物的准确重量，但他们预测的平均值是 1197 磅。

在机器学习领域，我们也采用了类似的减少错误的想法。

2. Bootstrapping

Bagging (也称为 Bootstrap aggregation) 是最早，也是最基本的集成技术之一。它是由 Leo Breiman 在 1994 年提出的。Bagging 是基于自举的统计方法，这使得对复杂模型的许多统计评估变得可行。

Bootstrap 方法如下。设大小为 N 的样本 X。我们可以通过随机均匀的从训练集中抽取 N 个元素，作为采集池。换句话说，我们从大小为 N 的原始样本中随机选择几个元素，并且放回，重复进行几次。所以，每个元素被抽取到的概率都是 $\frac{1}{N}$ 。

假设我们一个人从一个袋子里面拿球。在每个步骤中，将所选择的球放回到袋子中，以便相应的进行下一次选择，即从相同数量的球 N 开始。请注意，因为我们将球是放回的，所以新样本中可能存在重复。我们称这个新样本为 $X_1$ 。

通过重复该过程 M 次，我们创建 M 个采集样本 $X_1,X_2,\dots ,X_M$ 。最后，我们有足够数量的样本，可以计算原始分布的各种统计数据。

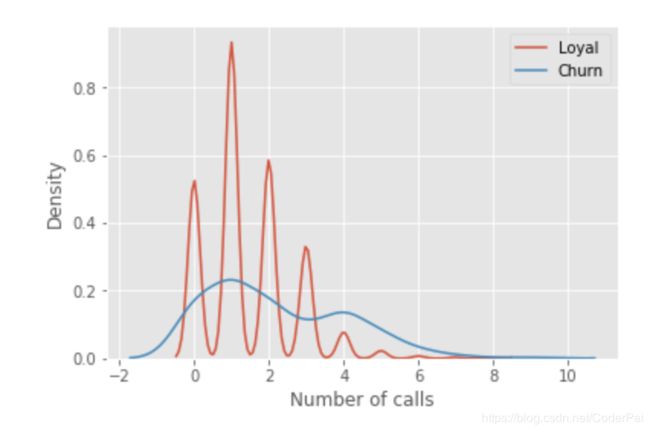
对于我们的例子，我们将使用熟悉的 telecom_churn 数据集。以前，当我们讨论特征重要性的时候，我们发现此数据集中最重要的特征之一就是对客户服务的调用次数。让我们可视化看一下数据，并且分析一下数据的分布状态。

import pandas as pd
from matplotlib import pyplot as plt
plt.style.use('ggplot')
plt.rcParams['figure.figsize'] = 10, 6
import seaborn as sns
%matplotlib inline

telecom_data = pd.read_csv('../input/telecom_churn.csv')

fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == False]['Customer service calls'], label = 'Loyal')
fig = sns.kdeplot(telecom_data[telecom_data['Churn'] == True]['Customer service calls'], label = 'Churn')        
fig.set(xlabel='Number of calls', ylabel='Density')    
plt.show()

正如你所看到的，忠诚的客户对客户服务的呼叫次数少于组中离开的客户。现在，估计每个组中的平均客户服务呼叫数量可能是个好主意。由于我们的数据集很小，所以我们不会通过简单的计算原始样本的平均值来获得良好的估计。我们最好应用 bootstrap 方法。让我们从原始群体中生成 1000 个新的样本，并生成平均值的区间估计值。

import numpy as np

def get_bootstrap_samples(data, n_samples):
    """Generate bootstrap samples using the bootstrap method."""
    indices = np.random.randint(0, len(data), (n_samples, len(data)))
    samples = data[indices]
    return samples

def stat_intervals(stat, alpha):
    """Produce an interval estimate."""
    boundaries = np.percentile(stat, [100 * alpha / 2., 100 * (1 - alpha / 2.)])
    return boundaries

# Save the data about the loyal and former customers to split the dataset
loyal_calls = telecom_data[telecom_data['Churn'] == False]['Customer service calls'].values
churn_calls= telecom_data[telecom_data['Churn'] == True]['Customer service calls'].values

# Set the seed for reproducibility of the results
np.random.seed(0)

# Generate the samples using bootstrapping and calculate the mean for each of them
loyal_mean_scores = [np.mean(sample) 
                       for sample in get_bootstrap_samples(loyal_calls, 1000)]
churn_mean_scores = [np.mean(sample) 
                       for sample in get_bootstrap_samples(churn_calls, 1000)]

# Print the resulting interval estimates
print("Service calls from loyal: mean interval", stat_intervals(loyal_mean_scores, 0.05))
print("Service calls from churn: mean interval", stat_intervals(churn_mean_scores, 0.05))

Service calls from loyal: mean interval [ 1.4077193   1.49473684]
Service calls from churn: mean interval [ 2.0621118   2.39761905]

最后，我们看到， 95% 的置信度，来自于忠诚客户的平均客户服务电话数量在 1.4 到 1.49 之间，而被调查的客户平均数为 2.06 到 2.4 。此外，请注意忠诚客户的间隔时间较窄，这是合理的，因为与被调用的客户相比，他们拨打的电话数量较少(0，1或者2)，知道他们变得厌倦或者转换供应商为止。

3. bagging

现在你已经学习了，如何去采样，接下来我们就可以继续学习 bagging 算法了。

假设，我们有一个训练集 X，利用自举，我们生成样本 $X_1,X_2,\dots ,X_M$ 。现在，为每一个自举的样本，我们都去训练一个专属于它的分类器 $a_i(x)$ 。最终的分类器是平均所有这些单独分类器的输出。在分类算法中，这种技术称之为投票：

$a(x)=\frac{1}{M}{\sum }_{i=1}^M{a}_i(x)$

下面的图片展示了整个算法的流程：

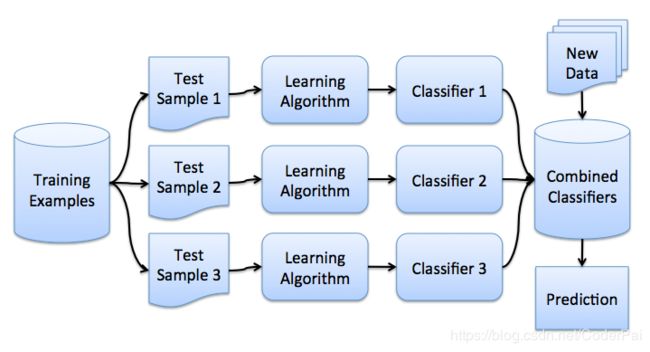
让我们考虑一个回归问题，并且设计每个基算法为 $b_1(x),b_2(x),\dots ,b_n(x)$ 。假设存在为所有输入定义的一个真实答案 $y(x)$ ，也就是我们的目标函数，并且数据的分布为 $p(x)$ 。那么我们可以表达每个回归函数的误差如下所示：

${ϵ}_i(x)=b_i(x)-y(x),i=1,\dots ,n$

并且均方误差的预期值为：

$E_x[(b_i(x)-y(x){)}^2]=E_x[{ϵ}_i^2(x)]$

然后，所有回归函数的平均误差如下：

$E_1=\frac{1}{n}{E}_x[\sum {ϵ}_i^2(x)]$

我们假设误差是无偏差的，并且不相关的，即：

$E_x[{ϵ}_i(x)]=0$

$E_x[{ϵ}_i(x){ϵ}_j(x)]=0,i̸=j$

现在，让我们构建一个新的回归函数，它将对各个函数的值进行平均计算：

$a(x)=\frac{1}{n}{\sum }_{i=1}^n{b}_i(x)$

让我们找到他的均方误差：

因此，通过平均各个输出答案，我们将均方误差减少了 n 倍。

让我们回想一下，总样本误差的公式为：

当我们在不同数据集上面进行训练模型时，Bagging 通过减少误差的方差来降低误差。换句话说，bagging 模型能降低过拟合。bagging 能起到这种效果是因为：由于各个数据集是不同的，所以在投票的环节他们的误差被相互抵消了。另外，在一些采样数据中，异常值可能就直接被忽略了。

scikit-learn 库支持使用元估计 BaggingRegressor 和 BaggingClassifier 进行 Bagging 学习。你可以使用大多数算法作为 Bagging 算法的基础。

让我们来看看 Bagging 在实践中是如何工作的，并将其与决策树进行比较。为此，我们将使用 sklearn 文档中的例子。

决策树的误差为：

$0.0255(Err)=0.0003(Bia{s}^2)+0.0152(Var)+0.0098({\sigma }^2)$

Bagging 的误差为：

$0.0196(Err)=0.0004(Bia{s}^2)+0.0092(Var)+0.0098({\sigma }^2)$

从上图中可以看出，Bagging 误差中的方差比决策树要小很多。请记住，我们已经在理论层面证明了这一点。

Bagging 算法对小样本数据集是非常有效的。甚至丢弃训练数据的一小部分构建异构数据集也是可以的。如果你有一个大型数据集，则可以考虑生成尺寸小得多的 bootstrap 样本。

上面的例子不太可能适用于任何实际工作。这是因为我们强烈假设我们的个体错误是不相关的。通常情况下，这对于实际应用来说过于乐观了。当这个假设是错误的时候，误差的减少将不能买显著。后续文章，我们会讨论一些更加复杂的集成学习方法，这些方法在现实问题中实现更加准确的预测。

4. OOB 错误(out of bag error)

在我们处理数据实验时，总会去做一个验证集来保证我们模型的适用性。但是在我们这个 bagging 算法的情况下，我们不需要适用交叉验证或者保持一定的样本以获得无偏差错误估计，这是为什么呢？因为，在集成技术中，误差估计已经在内部发生了。

使用原始数据集的不同采集样本来构造随机树。大约 37% 的输入被排除在特定的 bootstrap 样本之外，并且不用于构造第 k 个树。

这很容易证明，假设我们的数据集中有 $\ell$ 个数据，在每个步骤中，每个数据点都有相同的概率被取到，概率为 $\frac{1}{\ell }$ 。没有包含这种元素的概率是 $(1-\frac{1}{\ell }{)}^{\ell }$ ，当 $\ell \to +\infty$ ，这个值就无限接近于 $\frac{1}{e}$ ，然后，选择特定数据的概率就是 $1-\frac{1}{e}\approx 63$ 。

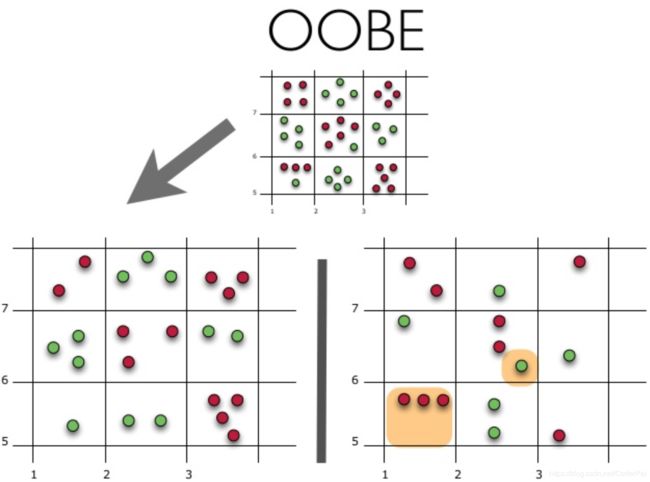
让我们直观的了解 OOBE 估算是如何工作的：

上图的上半部分代表我们的原始数据集，我们将它分为训练(左)和测试(右)组。在作图中，我们绘制了一个网格，根据类完美的划分我们的数据集。现在，我们使用相同的网络来估计测试集上正确答案的份额。我们可以看到，我们的分类器在训练期间未使用的 4 个案例中给出了错误预测(左侧)，因此，我们的分类器的准确度为 $\frac{11}{15}=73.33 % $

总而言之，每个基本算法都在原始例子的约 63% 上进行训练。它可以在剩余的37% 上进行验证。OOB 估计只不过是基础算法的平均估计值，那些 37% 的输入被排除在训练之外。