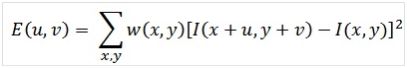图像平滑处理，6种滤波总结;

图像平滑处理，6种滤波总结的综合示例

【盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波导向滤波】

本文力求用最简洁的语言，详细的代码将此部分内容讲解清楚，但由于博主同样是刚刚接触OpenCV，或许表达上有些瑕疵，还望读者能够指教探讨，大家共同进步。

机器配置为：VS2017+opencv3.2.0+Win-64bit。

若本文能给读者带来一点点启示与帮助，我就很开心了。

====================分割线====================

1-图像滤波

• 1.图像滤波，即在尽量保留图像细节特征的条件下对目标图像的噪声进行抑制，是图像预处理中不可缺少的操作，其处理效果的好坏将直接影响到后续图像处理和分析的有效性和可靠性。
• 2.消除图像中的噪声成分叫作图像的平滑化或滤波操作。信号或图像的能量大部分集中在幅度谱的低频和中频段是很常见的，而在较高频段，感兴趣的信息经常被噪声淹没。因此一个能降低高频成分幅度的滤波器就能够减弱噪声的影响。
• 3.平滑滤波是低频增强的空间域滤波技术。它的目的有两类：一类是模糊；另一类是消除噪音。空间域的平滑滤波一般采用简单平均法进行，就是求邻近像元点的平均亮度值。邻域的大小与平滑的效果直接相关，邻域越大平滑的效果越好，但邻域过大，平滑会使边缘信息损失的越大，从而使输出的图像变得模糊，因此需合理选择邻域的大小。
• 4.关于滤波器，一种形象的比喻法是：我们可以把滤波器想象成一个包含加权系数的窗口，当使用这个滤波器平滑处理图像时，就把这个窗口放到图像之上，透过这个窗口来看我们得到的图像。
• 滤波目的：

• 1、消除图像中混入的噪声。2、为图像识别抽取出图像特征。

滤波要求：

• 1、不能损坏图像轮廓及边缘 。2、图像视觉效果应当更好。

滤波器的种类有很多， 本文结合前几节的内容，写了个综合示例，包含6种滤波方法：

盒式滤波、平滑处理1线性滤波之——盒式滤波（方框滤波）

均值滤波、平滑处理2线性滤波之——均值滤波

高斯滤波、平滑处理3线性滤波之——高斯滤波

中值滤波、平滑处理4非线性滤波之——中值滤波

双边滤波、平滑处理5非线性滤波之——双边滤波

导向滤波、平滑处理6——引导滤波/导向滤波（Guided Filter）

其中阈值量可通过滑动条来调节，下面来看看程序是如何实现的。

=======================分割线====================

2-代码演示

 

[cpp] view plain copy

1. /* 
2.     功能：用滚动条来控制6种滤波方式的参数值。 
3.           盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波、导向滤波。 
4. */  
5. #include                       
6. #include           
7. #include       
8. #include          
9. using namespace std;  
10. using namespace cv;  
11.   
12. #define WINDOWNAME "【滤波处理结果窗口】"  
13.   
14. //---------------【全局变量声明部分】-------------------------  
15. Mat g_srcIamge, g_dstImage1, g_dstImage2, g_dstImage3, g_dstImage4, g_dstImage5, g_dstImage6;  
16. int g_nBoxFilterValue = 1;//盒式滤波内核值  
17. int g_nMeanBlurValue = 1;//均值滤波内核值  
18. int g_nGaussianBlurValue = 1;//高斯滤波内核值  
19. int g_nMedianBlurValue = 1;//中值滤波内核值  
20. int g_nBilateralFilterValue = 1;//双边滤波内核值  
21. int g_nGuidedFilterValue = 1;//导向滤波内核值  
22. const int g_nMaxVal = 20; //预设滑动条最大值   
23. //--------------【全局函数声明部分】-------------------------  
24. //轨迹条回调函数  
25. static void on_BoxFilter(int, void*);//盒式滤波器  
26. static void on_MeanBlur(int, void*);//均值滤波器  
27. static void on_GaussianBlur(int, void*);//高斯滤波器  
28. static void on_MedianBlur(int, void*);//中值滤波器  
29. static void on_BilateralFilter(int, void*);//双边滤波器  
30. static void on_GuidedFilter(int, void*);//导向滤波器  
31. void guidedFilter(Mat &srcMat, Mat &guidedMat, Mat &dstImage, int radius, double eps);//导向滤波器  
32.   
33. //----------------------------【主函数】---------------------------  
34. int main()  
35. {  
36.     //------------【1】读取源图像并检查图像是否读取成功------------    
37.     g_srcIamge = imread("D:\\OutPutResult\\ImageTest\\boatLong.jpg");  
38.     if (!g_srcIamge.data)  
39.     {  
40.         cout << "读取图片错误，请重新输入正确路径！\n";  
41.         system("pause");  
42.         return -1;  
43.     }  
44.     namedWindow("【源图像】", 1);//创建窗口  
45.     imshow("【源图像】", g_srcIamge);//显示窗口  
46.     //------------【2】在WINDOWNAME窗口上分别创建滤波6个滑动条------------         
47.     namedWindow(WINDOWNAME);//创建窗口    
48.     createTrackbar("方框滤波", WINDOWNAME, &g_nBoxFilterValue, g_nMaxVal, on_BoxFilter);//创建方框滤波轨迹条  
49.     on_BoxFilter(g_nBoxFilterValue, 0); //轨迹条的回调函数  
50.     createTrackbar("均值滤波", WINDOWNAME, &g_nMeanBlurValue, g_nMaxVal, on_MeanBlur);//创建均值滤波轨迹条  
51.     on_MeanBlur(g_nMeanBlurValue, 0);  
52.     createTrackbar("高斯滤波", WINDOWNAME, &g_nGaussianBlurValue, g_nMaxVal, on_GaussianBlur);//创建高斯滤波轨迹条  
53.     on_GaussianBlur(g_nGaussianBlurValue, 0);  
54.     createTrackbar("中值滤波", WINDOWNAME, &g_nMedianBlurValue, g_nMaxVal, on_MedianBlur);//创建中值滤波轨迹条  
55.     on_MedianBlur(g_nMedianBlurValue, 0);  
56.     createTrackbar("双边滤波", WINDOWNAME, &g_nBilateralFilterValue, g_nMaxVal, on_BilateralFilter);//创建双边滤波轨迹条  
57.     on_BilateralFilter(g_nBilateralFilterValue, 0);  
58.     createTrackbar("导向滤波", WINDOWNAME, &g_nGuidedFilterValue, g_nMaxVal, on_GuidedFilter);//创建导向滤波轨迹条  
59.     on_GuidedFilter(g_nGuidedFilterValue, 0);  
60.     //------------【3】退出程序------------    
61.     cout << "\t按下'q'键，退出程序~！\n" << endl;  
62.     while (char(waitKey(1)) != 'q'){}  
63.     return 0;  
64. }  
65.   
66. //----------------------【on_BoxFilter()函数】------------------------  
67. static void on_BoxFilter(int, void*)  
68. {  
69.     boxFilter(g_srcIamge, g_dstImage1, -1, Size(g_nBoxFilterValue * 2 + 1, g_nBoxFilterValue * 2 + 1));  
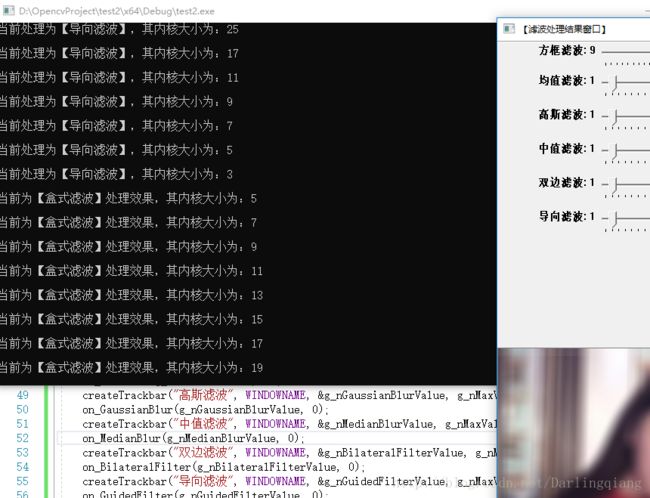
70.     cout << "\n当前为【盒式滤波】处理效果，其内核大小为：" << g_nBoxFilterValue * 2 + 1 << endl;  
71.     imshow(WINDOWNAME, g_dstImage1);  
72. }  
73. //----------------------【on_MeanBlur()函数】------------------------  
74. static void on_MeanBlur(int, void*)  
75. {  
76.     blur(g_srcIamge, g_dstImage2, Size(g_nMeanBlurValue * 2 + 1, g_nMeanBlurValue * 2 + 1), Point(-1, -1));  
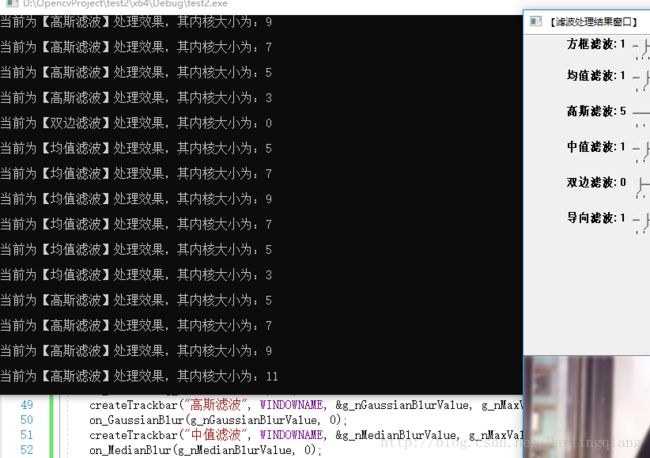
77.     cout << "\n当前为【均值滤波】处理效果，其内核大小为：" << g_nMeanBlurValue * 2 + 1 << endl;  
78.     imshow(WINDOWNAME, g_dstImage2);  
79. }  
80. //----------------------【on_GaussianBlur()函数】------------------------  
81. static void on_GaussianBlur(int, void*)  
82. {  
83.     GaussianBlur(g_srcIamge, g_dstImage3, Size(g_nGaussianBlurValue * 2 + 1, g_nGaussianBlurValue * 2 + 1), 0, 0);  
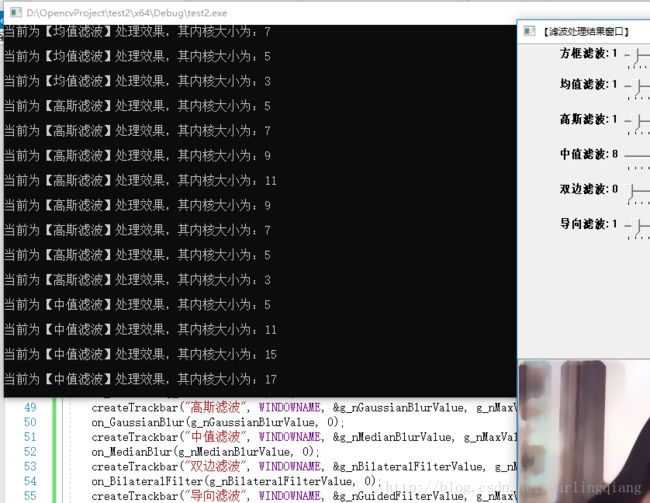
84.     cout << "\n当前为【高斯滤波】处理效果，其内核大小为：" << g_nGaussianBlurValue * 2 + 1 << endl;  
85.     imshow(WINDOWNAME, g_dstImage3);  
86. }  
87. //----------------------【on_MedianBlur()函数】------------------------  
88. static void on_MedianBlur(int, void*)  
89. {  
90.     medianBlur(g_srcIamge, g_dstImage4, g_nMedianBlurValue * 2 + 1);  
91.     cout << "\n当前为【中值滤波】处理效果，其内核大小为：" << g_nMedianBlurValue * 2 + 1 << endl;  
92.     imshow(WINDOWNAME, g_dstImage4);  
93. }  
94. //----------------------【on_BilateralFilter()函数】------------------------  
95. static void on_BilateralFilter(int, void*)  
96. {  
97.     bilateralFilter(g_srcIamge, g_dstImage5, g_nBilateralFilterValue, g_nBilateralFilterValue * 2, g_nBilateralFilterValue / 2);  
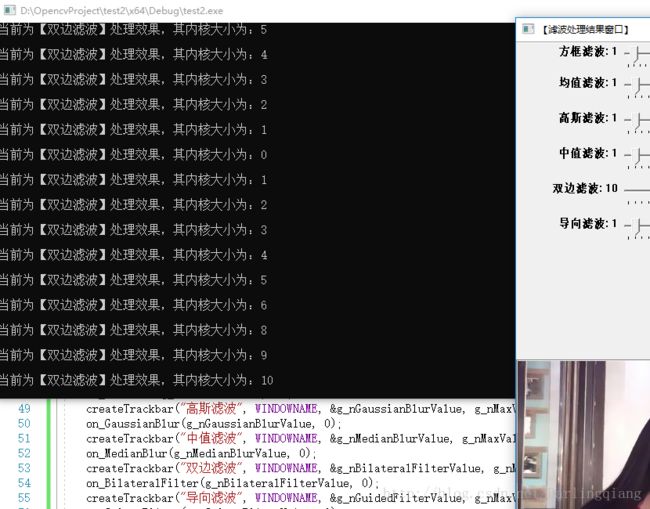
98.     cout << "\n当前为【双边滤波】处理效果，其内核大小为：" << g_nBilateralFilterValue << endl;  
99.     imshow(WINDOWNAME, g_dstImage5);  
100. }  
101. //----------------------【on_GuidedFilter()函数】------------------------  
102. static void on_GuidedFilter(int, void*)  
103. {  
104.     vector vSrcImage, vResultImage;  
105.     //【1】对源图像进行通道分离，并对每个分通道进行导向滤波操作  
106.     split(g_srcIamge, vSrcImage);  
107.     for (int i = 0; i < 3; i++)  
108.     {  
109.         Mat tempImage;  
110.         vSrcImage[i].convertTo(tempImage, CV_64FC1, 1.0 / 255.0);//将分通道转换成浮点型数据  
111.         Mat cloneImage = tempImage.clone(); //将tempImage复制一份到cloneImage  
112.         Mat resultImage;  
113.         guidedFilter(tempImage, cloneImage, resultImage, g_nGuidedFilterValue * 2 + 1, 0.01);//对分通道分别进行导向滤波  
114.         vResultImage.push_back(resultImage);//将分通道导向滤波后的结果存放到vResultImage中  
115.     }  
116.     //【2】将分通道导向滤波后结果合并  
117.     merge(vResultImage, g_dstImage6);  
118.     cout << "\n当前处理为【导向滤波】，其内核大小为：" << g_nGuidedFilterValue * 2 + 1 << endl;  
119.     imshow(WINDOWNAME, g_dstImage6);  
120. }  
121.   
122. //-------------------【实现导向滤波器函数部分】-------------------------  
123. void guidedFilter(Mat &srcMat, Mat &guidedMat, Mat &dstImage, int radius, double eps)  
124. {  
125.     //------------【0】转换源图像信息，将输入扩展为64位浮点型，以便以后做乘法------------  
126.     srcMat.convertTo(srcMat, CV_64FC1);  
127.     guidedMat.convertTo(guidedMat, CV_64FC1);  
128.     //--------------【1】各种均值计算----------------------------------  
129.     Mat mean_p, mean_I, mean_Ip, mean_II;  
130.     boxFilter(srcMat, mean_p, CV_64FC1, Size(radius, radius));//生成待滤波图像均值mean_p   
131.     boxFilter(guidedMat, mean_I, CV_64FC1, Size(radius, radius));//生成导向图像均值mean_I     
132.     boxFilter(srcMat.mul(guidedMat), mean_Ip, CV_64FC1, Size(radius, radius));//生成互相关均值mean_Ip  
133.     boxFilter(guidedMat.mul(guidedMat), mean_II, CV_64FC1, Size(radius, radius));//生成导向图像自相关均值mean_II  
134.     //--------------【2】计算相关系数，计算Ip的协方差cov和I的方差var------------------  
135.     Mat cov_Ip = mean_Ip - mean_I.mul(mean_p);  
136.     Mat var_I = mean_II - mean_I.mul(mean_I);  
137.     //---------------【3】计算参数系数a、b-------------------  
138.     Mat a = cov_Ip / (var_I + eps);  
139.     Mat b = mean_p - a.mul(mean_I);  
140.     //--------------【4】计算系数a、b的均值-----------------  
141.     Mat mean_a, mean_b;  
142.     boxFilter(a, mean_a, CV_64FC1, Size(radius, radius));  
143.     boxFilter(b, mean_b, CV_64FC1, Size(radius, radius));  
144.     //---------------【5】生成输出矩阵------------------  
145.     dstImage = mean_a.mul(srcMat) + mean_b;  
146. }  

========================分割线====================

 

3-显示结果

原始图像窗口，如下图：

 

盒式滤波/方框滤波操作，如下图：

 

均值滤波操作，如下图：

 

高斯滤波操作，如下图：

 

中值滤波操作，如下图：

 

双边滤波操作，如下图：

导向滤波操作，如下图：

 

=====================分割线==================

4-程序说明

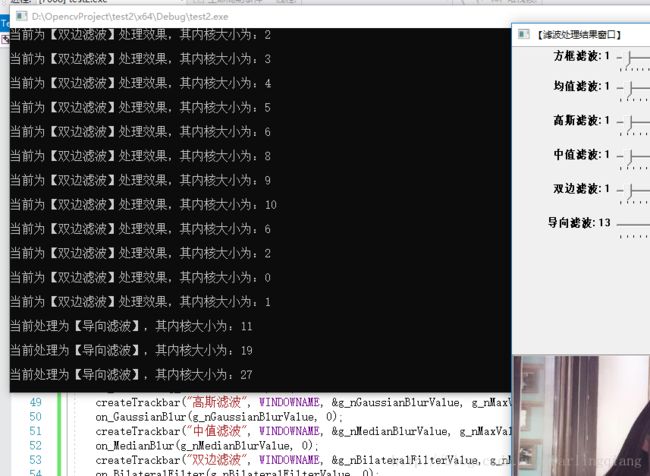
【滤波处理结果窗口】中显示的数值并非实际内核大小，真正内核大小还请看黑窗口的提示信息。

其中前五种滤波方式：盒式滤波、均值滤波、高斯滤波、中值滤波、双边滤波，OpenCV都已封装在函数里了，我们直接调用即可，而导向滤波，是需要自己编写，然后调用即可。

 

为了便于观察各种滤波方式的效果优缺点，我对原图进行了处理，左边的图像是添加了椒盐噪声，而右边的图像是添加了高斯噪声，同学们可以通过滑动条调节，试试看每种滤波方式对噪声的处理结果是如何情况。

 

====END===================

 

角点检测（Harris,Fast,surf）

前面分析了Sift算法的具体原理，就顺便想看看其他的角点检测算法，和对比。这些看完之后，相比sift的原理比较简单.

Harris:

这个算法通过两张图就看得很清楚了。将被检测点上的window移动一下，然后计算原来的window和移动之后的window对应位置像素差的平方和，如果变化不大说明这个点在物体内部，如果一个方向上变化大，另外一个方向上变化不大说明在边界上。如果任何方向上变化都很大说明这个点就是corner point。

但是这个方法效果不是很好，主要存在两方面的问题：

1. .0-1window对噪声比较敏感
2. window移动的方向太少，导致该算法对边缘敏感（准确的说是和window移动方向不一致的边缘）

harris（1988）harris（1988）年提出了改进方案。

1. 将01window改成了Gaussian window，中心权重比较高，离中心越远权重越低。
2. 使用泰勒展开考虑所有方向

通过泰勒展开可以将原window和shift之后的window对应位置像素差的平方和表示为移动方向*该点Hessian矩阵*移动方向。Hessian矩阵的较大特征值和对应特征向量分别表示变化最大方向和对应变化幅度。第二特征值和对应特征向量，表示和变化最大方向相垂直的方向以及该方向变化的幅度。如果最大特征值很小那么说明该点在物体内部；如果第一特征值很大，另外一个特征值接近零说明该点是一个edge point；如果两个特征值都远大于零说明该点是一个corner point。
Harris 为了简化计算提出了一个cornerness的量，越大越说明这个点越corner

角点计算数学原理：

基本数学公式如下：

其中W(x, y)表示移动窗口，I(x, y)表示像素灰度值强度，范围为0～255。根据泰勒级数，计算一阶到N阶的偏导数，最终得到一个Harris矩阵公式：

根据Harris的矩阵计算矩阵特征值,然后计算Harris角度响应值：

其中K为系数值，通常取值范围为0.04 ~ 0.06之间。

算法详细步骤

1. 计算图像X方向与Y方向的一阶高斯偏导数Ix与Iy
2. 根据第一步结果得到Ix^2 , Iy^2与Ix*Iy值
3. 高斯模糊第二步三个值得到Sxx, Syy, Sxy
4. 定义每个像素的Harris矩阵，计算出矩阵的两个特质值
5. 计算出每个像素的R值
6. 使用3X3或者5X5的窗口，实现非最大值压制
7. 根据角度检测结果计算，最提取到的关键点以绿色标记，显示在原图上。

Fast角点检测：

Edward Rosten and TomDrummond 在2006年提出了一种简单快速的角点探测算法，该算法检测的角点定义为在像素点的周围邻域内有足够多的像素点与该点处于不同的区域。应用到灰度图像中，即有足够多的像素点的灰度值大于该点的灰度值或者小于该点的灰度值。

考虑下图中p点附近半径为3的圆环上的16个点，一个思路是若其中有连续的12个点的灰度值与p点的灰度值差别超过某一阈值，则可以认为p点为角点。

这一思路可以使用机器学习的方法进行加速。对同一类图像，例如同一场景的图像，可以在16个方向上进行训练，得到一棵决策树，从而在判定某一像素点是否为角点时，不再需要对所有方向进行检测，而只需要按照决策树指定的方向进行2-3次判定即可确定该点是否为角点。

常见的角点检测算法比较：

 

　　图像匹配能够应用的场合非常多，如目标跟踪，检测，识别，图像拼接等，而图像匹配最核心的技术就要属角点匹配了，所谓角点匹配是指寻找两幅图像之间的特征像素点的对应关系，从而确定两幅图像的位置关系。

　　角点匹配可以分为以下四个步骤：

1. 提取检测子：在两张待匹配的图像中寻找那些最容易识别的像素点（角点），比如纹理丰富的物体边缘点等。　
2. 提取描述子：对于检测出的角点，用一些数学上的特征对其进行描述，如梯度直方图，局部随机二值特征等。
3. 检测子和描述子的常用提取方法有:sift, harris, surf, fast, agast, brisk, freak, brisk,orb等。　
4. .匹配：通过各个角点的描述子来判断它们在两张图像中的对应关系。常用方法如 flann　　
5. 去外点：去除错误匹配的外点，保留正确的内点。常用方法有Ransac, GTM。

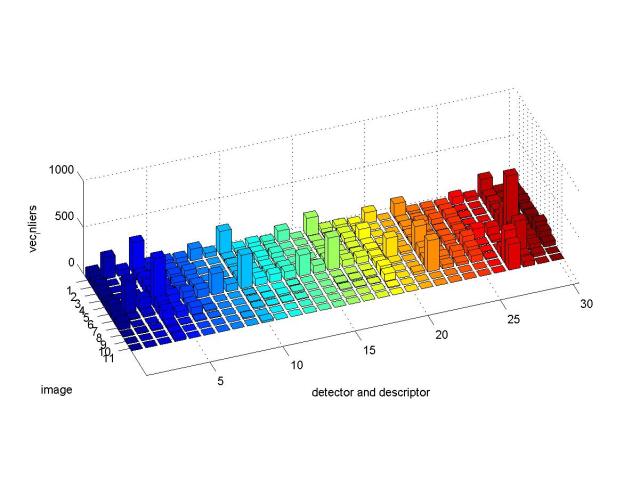
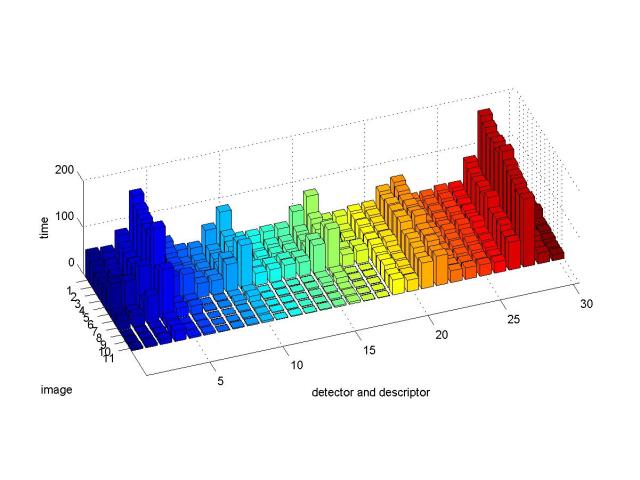
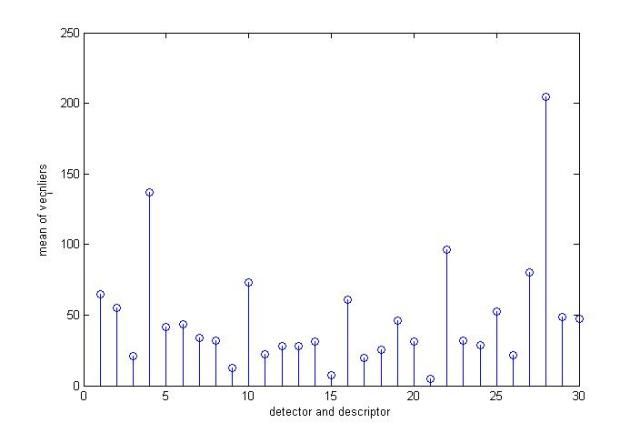
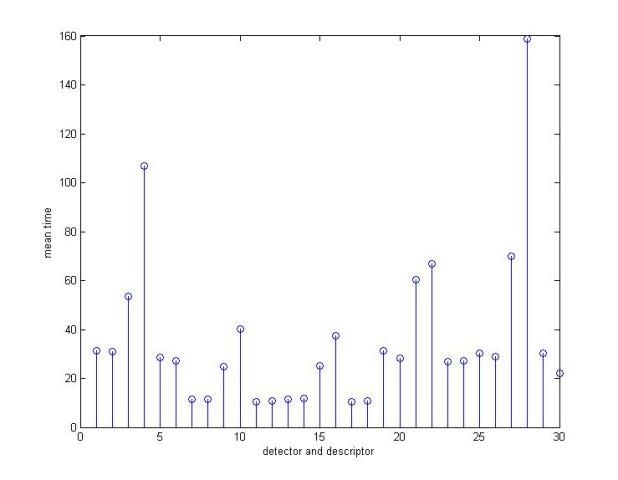
　　我对上述这些常用的检测子和描述子的性能和速度做了一个测试，以找出其中性价比最好的组合（不考虑后两步）

　　　　　　　　　　　　　　　　　　　　　　　　图一

 

　　　　　　　　　　　　　　　　　　　　　　图二

　　上面两幅图是对上述部分检测子与描述子进行测试的结果。

　　其中图一和图二的x坐标表示不同的检测子与描述子的组合，从1到30分别对应

(surf、agast、brisk、fast、sift、orb)检测子与 (brisk、agast、surf、sift、orb)描述子的线性组合，如第四组表示surf检测子+sift描述子的组合。

　　图一和图二的y坐标表示一系列测试图片组，每组由两张图组成，这些图片都是质量较低的卫星地图，约2000*2000像素，每组的两张图片是由不同卫星对地面上同一地区进行拍摄的。它们之间的关系可能包含旋转，缩放，仿射变换，亮度变化，模糊，噪音等。从1到11的测试图片组大概对应着以下变换关系:

1. 强烈亮度变化
2. 旋转
3. 仿射变换+尺度变化+旋转
4. 仿射变换+亮度变化+旋转
5. 仿射变换+噪音
6. 模糊+亮度变化
7. 旋转+噪音
8. 旋转+尺度变化
9. 亮度变化+旋转+模糊+噪音
10.  亮度变化+旋转+尺度变化
11.  亮度变化+旋转+尺度变化+强烈噪音。

　　图一的z坐标表示成功匹配的像素对的个数。图二的z坐标表示所需计算时间。

　　从测试结果来看，orb检测子与surf描述子配合的效果是最好的，不过速度也是最慢的。古老的sift和surf依然好用，速度也还是那么不给力。在不考虑旋转和仿射变换的情况下，fast是很不错的选择，在小幅旋转（20度内)的情况下，fast也还是有一定的容错能力的。在旋转变化和尺度变化方面，各家武功相差不多，虽然在理论上sift支持旋转变化，不过测试中它并没有表现出明显的优势。在噪音方面，sift和orb明显强于其它算法；在亮度变化和仿射变换上，orb的鲁棒性是最好的；综合比较，orb的性价比在此次华山论剑中略胜一筹。

　　下面两张图是上面11组图片的均值，从平均值来看，orb也是最好的

　　

 

　　

引用整理自blog:

1. ：http://blog.csdn.net/ben_ben_niao/article/details/47446627
2. （2）：http://blog.csdn.net/sinat_36264666/article/details/77823400
3. （3）：https://blog.csdn.net/xw20084898/article/details/21822565