循环神经网络 - - DeepLearning.ai 学习笔记(5-1)
课程笔记地址:https://blog.csdn.net/column/details/26931.html
课程代码地址:https://github.com/duboya/DeepLearning.ai-pragramming-code/tree/master
欢迎大家fork及star!(-O-)
序列模型 — 循环神经网络
1. 序列模型的应用
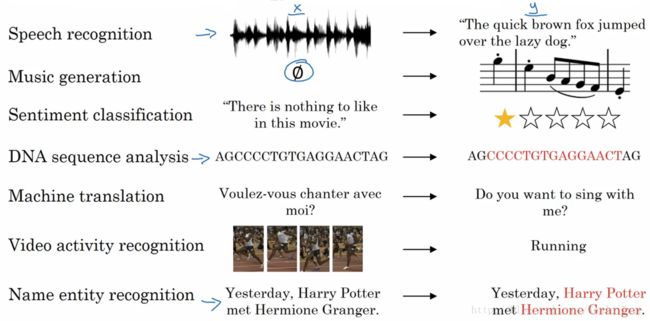
- 语音识别:将输入的语音信号直接输出相应的语音文本信息。无论是语音信号还是文本信息均是序列数据。
- 音乐生成:生成音乐乐谱。只有输出的音乐乐谱是序列数据,输入可以是空或者一个整数。
- 情感分类:将输入的评论句子转换为相应的等级或评分。输入是一个序列,输出则是一个单独的类别。
- DNA序列分析:找到输入的DNA序列的蛋白质表达的子序列。
- 机器翻译:两种不同语言之间的相互转换。输入和输出均为序列数据。
- 视频行为识别:识别输入的视频帧序列中的人物行为。
- 命名实体识别:从输入的句子中识别实体的名字。
2. 数学符号
- 输入x:如“Harry Potter and Herminone Granger invented a new spell.”(以序列作为一个输入), x < t > x^{<t>} x<t>表示输入 x 中的第 t 个符号。
- 输出y:如“1 1 0 1 1 0 0 0 0”(人名定位),同样,用 y < t > y^{<t>} y<t>表示输出 y 中的第 t 个符号。
- T x T_x Tx用来表示输入 x 的长度;
- T y T_y Ty用来表示输出 y 的长度;
- x ( i ) < t > x^{(i)<t>} x(i)<t>表示第 i 个输入样本的第 t 个符号,其余同理。
- 利用单词字典编码来表示每一个输入的符号:如one-hot编码等,实现输入 x 和输出 y 之间的映射关系。
3. 循环神经网络模型
传统标准的神经网络:
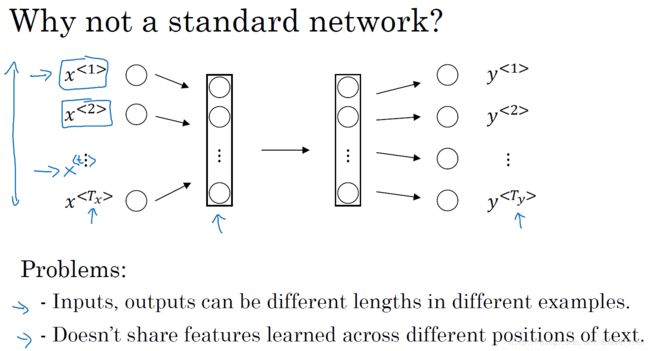
对于学习X和Y的映射,我们可以很直接的想到一种方法就是使用传统的标准神经网络。也许我们可以将输入的序列X以某种方式进行字典编码以后,如one-hot编码,输入到一个多层的深度神经网络中,最后得到对应的输出Y。如下图所示:
但是,结果表明这种方法并不好,主要是存在下面两个问题:
- 输入和输出数据在不同的例子中可以有不同的长度;(虽然可以采用padding将输入扩充为一致维度,但这种处理方式并不好,此外第二条问题不能共享文本不同位置学习到的特征则更为严重。)
- 这种朴素的神经网络结果并不能共享从文本不同位置所学习到的特征。(不能像卷积神经网络那样,将学到的特征的快速地推广到图片其他位置)
循环神经网络:
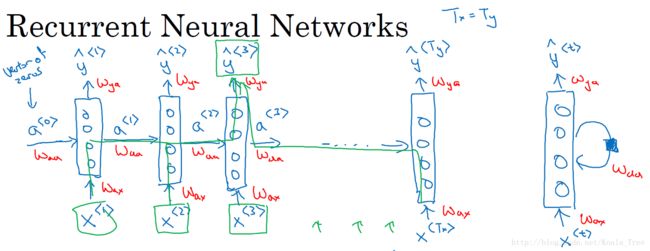
循环神经网络作为一种新型的网络结构,在处理序列数据问题上则不存在上面的两个缺点。在每一个时间步中,循环神经网络会传递一个激活值到下一个时间步中,用于下一时间步的计算。如下图所示:
这里需要注意在零时刻,我们需要编造一个激活值,通常输入一个零向量,有的研究人员会使用随机的方法对该初始激活向量进行初始化。同时,上图中右边的循环神经网络的绘制结构与左边是等价的。
循环神经网络是从左到右扫描数据的,同时共享每个时间步的参数。
- W a x W_{ax} Wax管理从输入 x < t > x^{<t>} x<t>到隐藏层的连接,每个时间步都使用相同的 W a x W_{ax} Wax,同下;
- W a a W_{aa} Waa管理激活值 a < t > a^{<t>} a<t>到隐藏层的连接;
- W y a W_{ya} Wya管理隐藏层到激活值 y < t > y^{<t>} y<t>的连接。
上述循环神经网络结构的缺点:每个预测输出 y < t > y^{<t>} y<t>仅使用了前面的输入信息,而没有使用后面的信息。Bidirectional RNN(双向循环神经网 络)可以解决这种存在的缺点。
循环神经网络的前向传播:
下图是循环神经网络结构图:
-
构造初始激活向量: a < 0 > = 0 → a^{<0>} = \overrightarrow{0} a<0>=0;
-
a < 1 > = g ( W a a a < 0 > + W a x x < 1 > + b a ) a^{<1>} = g(W_{aa}a^{<0>} + W_{ax}x^{<1>} + b_a) a<1>=g(Waaa<0>+Waxx<1>+ba); 通常选择 t a n h tanh tanh 作为激活函数,有时也会使用 R e l u Relu Relu 作为激活函数;(使用tanh函数梯度消失的问题会用其他方式解决)
-
y ^ < 1 > = g ( W y a a < 1 > + b y ) \widehat{y}^{<1>} = g(W_{ya}a^{<1>} + b_y) y <1>=g(Wyaa<1>+by);如果是二分类问题,使用sigmoid作为激活函数,如果是多分类问题,可以使用softmax激活函数;
注:其中 W a x W_{ax} Wax中,前面的a表示要得到一个a类型的量,x表示参数W要乘以一个x类型的量,其余 W a a W_{aa} Waa、 W y a W_{ya} Wya同理;
a < t > = g ( W a a a < t − 1 > + W a x x < t > + b a ) y ^ < t > = g ( W y a a < t > + b y ) a^{<t>} = g(W_{aa}a^{<t−1>} + W_{ax}x^{<t>} + b_a) \\ \widehat{y}^{<t>} = g(W_{ya}a^{<t>} + b_y) a<t>=g(Waaa<t−1>+Waxx<t>+ba)y <t>=g(Wyaa<t>+by)
上式是RNN的一般前向传播公式,我们还可以对上式进行简化:
a < t > = g ( W a [ a < t − 1 > , x < t > ] + b a ) y ^ < t > = g ( W y a < t > + b y ) a^{<t>} = g(W_{a}[a^{<t-1>},x^{<t>}] + b_a) \\ \widehat{y}^{<t>} = g(W_{y}a^{<t>} + b_y) a<t>=g(Wa[a<t−1>,x<t>]+ba)y <t>=g(Wya<t>+by)
其中:
- W a = [ W a a ⋮ W a x ] W_a = [W_{aa} \vdots W_{ax}] Wa=[Waa⋮Wax],假如 a < t − 1 > a^{<t−1>} a<t−1>是100维, x < t > x^{<t>} x<t>是10000维,那么 W a a W_{aa} Waa便是(100,100)维的矩阵, W a x W_{ax} Wax便是(100,10000)维的矩阵。堆叠起来, W a W_a Wa便是(100,10100)维的矩阵。
- [ a , x ] = [ a < t − 1 > x < t > ] [a,x] = \begin{bmatrix} a^{<t-1>}\\x^{<t>} \end{bmatrix} [a,x]=[a<t−1>x<t>]表示一个(10100)维的矩阵。
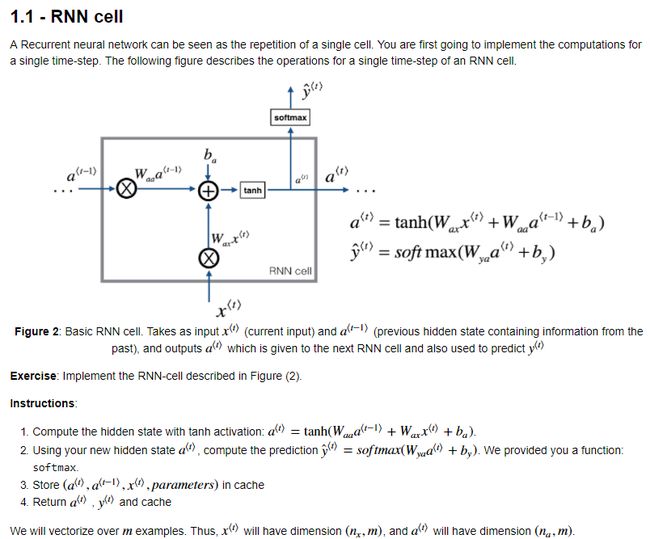
注:上述 a < t > a^{<t>} a<t>的表达式子中, [ a < t − 1 > , x < t > ] [a^{<t-1>},x^{<t>}] [a<t−1>,x<t>]表示是纵向的,如上一行公式所示,因此, a < t > a^{<t>} a<t>的表达式实际是[100, 1] = [100, 10100] * [10100, 1]。具体解释可参考下图。
RNN前馈解释图
摘选自本课课程作业。
4. 穿越时间的反向传播
为了进行反向传播计算,使用梯度下降等方法来更新RNN的参数,我们需要定义一个损失函数,如下:
L < t > ( y ^ < t > , y < t > ) = − y < t > l o g y ^ < t > − ( 1 − y < t > ) l o g ( 1 − y ^ < t > ) L ( y ^ , y ) = ∑ t = 1 T y L < t > ( y ^ < t > , y < t > ) L^{<t>}(\widehat{y}^{<t>},y^{<t>}) = −y^{<t>}log\widehat{y}^{<t>} − (1 − y^{<t>})log(1−\widehat{y}^{<t>}) \\ L(\widehat{y},y) = \sum_{t=1}^{T_y}L^{<t>}(\widehat{y}^{<t>},y^{<t>}) L<t>(y <t>,y<t>)=−y<t>logy <t>−(1−y<t>)log(1−y <t>)L(y ,y)=t=1∑TyL<t>(y <t>,y<t>)
上式表示将每个输出的损失进行求和即为整体的损失函数。反向传播算法按照前向传播相反的方向进行导数计算,来对参数进行更新。其中比较特别的是在RNN中,从右向左的反向传播计算是通过时间来进行,如穿越时间的反向计算。
- 损失函数使用logistic交叉熵损失函数
- 第一个式子是一个X(t)输出(对应到文本里面就是一个单词)的损失,第二个式子则是整个RNN网络的损失函数(即将各输入x(t)损失累加起来,从1到 T y T_y Ty)
5. 不同类型的RNN
对于RNN,不同的问题需要不同的输入输出结构。
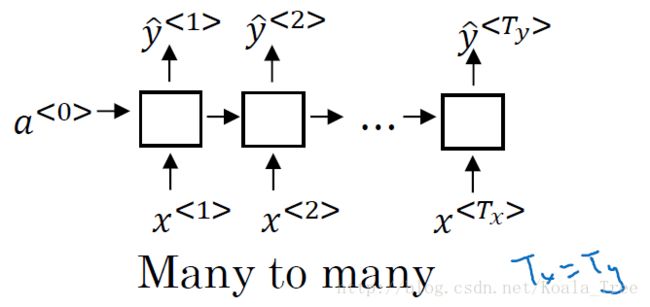
many-to-many( T x = T y T_x = T_y Tx=Ty):
这种情况下的输入和输出的长度相同,是上面例子的结构,如下图所示:
many-to-one:
如在情感分类问题中,我们要对某个序列进行正负判别或者打星操作。在这种情况下,就是输入是一个序列,但输出只有一个值:
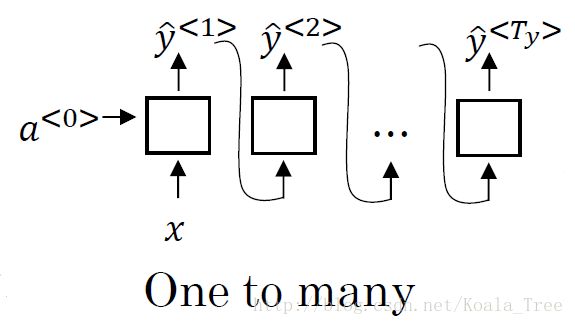
one-to-many:
如在音乐生成的例子中,输入一个音乐的类型或者空值,直接生成一段音乐序列或者音符序列。在这种情况下,就是输入是一个值,但输出是一个序列:
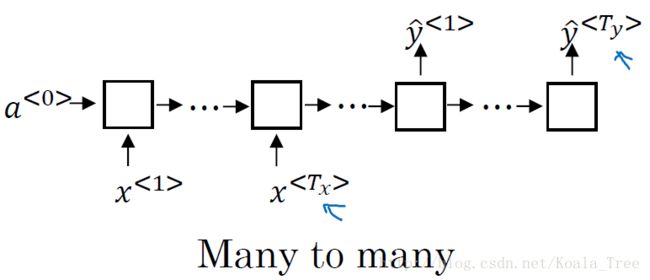
many-to-many( T x ≠ T y T_x \neq T_y Tx̸=Ty):
我们上面介绍的一种RNN的结构是输入和输出序列的长度是相同的,但是像机器翻译这种类似的应用来说,输入和输出都是序列,但长度却不相同,这是另外一种多对多的结构:
6. 语言模型和序列生成
在NLP中,构建语言模型是最基础也是最重要的工作之一,我们可以通过RNN来很好的实现。
什么是语言模型?
对于下面的例子,两句话有相似的发音,但是想表达的意义和正确性却不相同,如何让我们的构建的语音识别系统能够输出正确地给出想要的输出。也就是对于语言模型来说,从输入的句子中,评估各个句子中各个单词出现的可能性,进而给出整个句子出现的可能性。
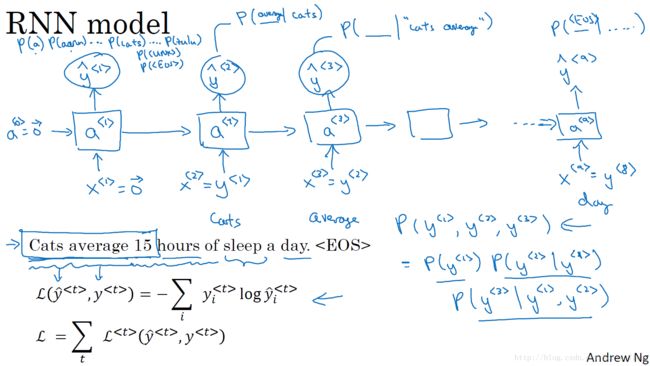
使用RNN构建语言模型:
- 训练集:一个很大的语言文本语料库;
- Tokenize:将句子使用字典库标记化;
- 其中,未出现在字典库中的词使用“UNK”来表示;
- 第一步:使用零向量对输出进行预测,即预测第一个单词是某个单词的可能性;
- 第二步:通过前面的输入,逐步预测后面一个单词出现的概率;
- 训练网络:使用softmax损失函数计算损失,对网络进行参数更新,提升语言模型的准确率。
7. 新序列采样
在完成一个序列模型的训练之后,如果我们想要了解这个模型学到了什么,其中一种非正式的方法就是进行一次新序列采样(sample novel sequences)。
对于一个序列模型,其模拟了任意特定单词序列的概率,如 P ( y < 1 > , ⋯ , y < T y > ) P(y^{<1>}, \cdots, y^{<Ty}>) P(y<1>,⋯,y<Ty>),而我们要做的就是对这个概率分布进行采样,来生成一个新的单词序列。
如下面的一个已经训练好的RNN结构,我们为了进行采样需要做的:
- 首先输入 x < 1 > = 0 , a < 0 > = 0 x^{<1>} = 0,a^{<0>} = 0 x<1>=0,a<0>=0,在这第一个时间步,我们得到所有可能的输出经过softmax层后可能的概率,根据这个softmax的分布,进行随机采样,获取第一个随机采样单词 y ^ < 1 > \widehat{y}^{<1>} y <1>;
- 然后继续下一个时间步,我们以刚刚采样得到的 y ^ < 1 > \widehat{y}^{<1>} y <1>作为下一个时间步的输入,进而softmax层会预测下一个输出 y ^ < 2 > \widehat{y}^{<2>} y <2>,依次类推;
- 如果字典中有结束的标志如:“EOS”,那么输出是该符号时则表示结束;若没有这种标志,则我们可以自行设置结束的时间步。
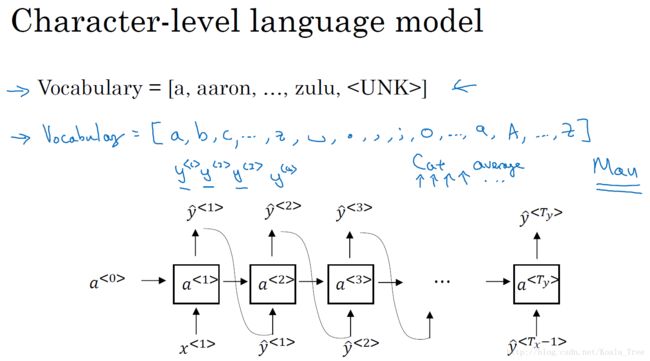
上面的模型是基于词汇的语言模型,我们还可以构建基于字符的语言模型,其中每个单词和符号则表示一个相应的输入或者输出:
但是基于字符的语言模型,一个主要的缺点就是我们最后会得到太多太长的输出序列,其对于捕捉句子前后依赖关系,也就是句子前部分如何影响后面部分,不如基于词汇的语言模型那样效果好;同时基于字符的语言模型训练代价比较高。所以目前的趋势和常见的均是基于词汇的语言模型。但随着计算机运算能力的增强,在一些特定的情况下,也会开始使用基于字符的语言模型。
8. RNN的梯度消失
RNN在NLP中具有很大的应用价值,但是其存在一个很大的缺陷,那就是梯度消失的问题。例如下面的例句中:
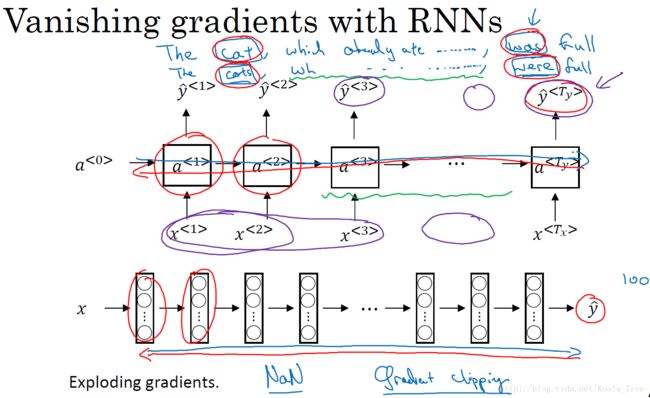
- The cat, which already ate …………,was full;
- The cats, which already ate …………,were full.
在这两个句子中,cat对应着was,cats对应着were,(中间存在很多很长省略的单词),句子中存在长期依赖(long-term dependencies),前面的单词对后面的单词有很重要的影响。但是我们目前所见到的基本的RNN模型,是不擅长捕获这种长期依赖关系的。
- 比如一个时间序列长度为1000的序列,对应RNN为1000层,这种情况下较长的依赖关系是难以维持的,因为与深度神经网络一样,当层数增加到一定数量之后就会存在梯度消失与梯度爆炸问题。
- 梯度爆炸问题相比于梯度消失更为容易发现(如梯度爆炸的话,往往会得到很多NaN或者数值溢出),也更容易解决一些,Ng介绍了一种方法叫做gradient clipping,也就是观察梯度向量,如果其大于某个阈值,则对其进行缩放,保证它不会太大。但梯度消失则更难以解决。
如下图所示,和基本的深度神经网络结构类似,输出y得到的梯度很难通过反向传播再传播回去,也就是很难对前面几层的权重产生影响,所以RNN也有同样的问题,也就是很难让网络记住前面的单词是单数或者复数,进而对后面的输出产生影响。
对于梯度消失问题,在RNN的结构中是我们首要关心的问题,也更难解决;虽然梯度爆炸在RNN中也会出现,但对于梯度爆炸问题,因为参数会指数级的梯度,会让我们的网络参数变得很大,得到很多的Nan或者数值溢出,所以梯度爆炸是很容易发现的,我们的解决方法就是用梯度修剪,也就是观察梯度向量,如果其大于某个阈值,则对其进行缩放,保证它不会太大。
9. GRU单元
门控循环单元(Gated Recurrent Unit, GRU)改变了RNN的隐藏层,使其能够更好地捕捉深层次连接,并改善了梯度消失的问题。
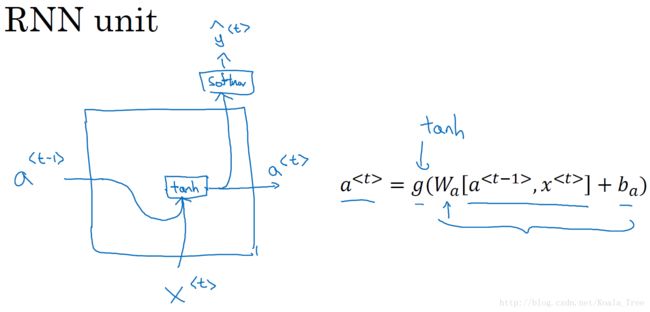
RNN 单元:
对于RNN的一个时间步的计算单元,在计算 a < t > a^{<t>} a<t>也就是下图右边的公式,能以左图的形式可视化呈现:
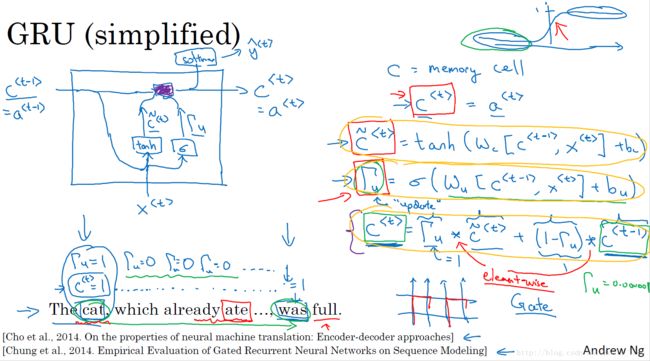
简化的GRU 单元:
我们以时间步从左到右进行计算的时候,在GRU单元中,存在一个新的变量称为c, (代表cell), 作为“记忆细胞”,其提供了长期的记忆能力。
- c < t > = a < t > c^{<t>} = a^{<t>} c<t>=a<t>,实际上记忆细胞输出的是在t时间步上的激活值a;
- c ~ < t > = t a n h ( W c [ c < t − 1 > , x < t > ] + b c ) \tilde{c}^{<t>} = tanh(W_c[c^{<t−1>}, x^{<t>}] + b_c) c~<t>=tanh(Wc[c<t−1>,x<t>]+bc),在每一个时间步上,给定一个候选值 c ~ < t > \tilde{c}^{<t>} c~<t>,用以替代原本的记忆细胞 c < t > c^{<t>} c<t>;
- Γ u = σ ( W u [ c < t − 1 > , x < t > ] + b u ) \Gamma_u = \sigma(W_u[c^{<t−1>}, x^{<t>}] + b_u) Γu=σ(Wu[c<t−1>,x<t>]+bu),代表更新门,是一个0-1的值,用以决定是否对当前时间步的记忆细胞用候选值更新替代;
- c < t > = Γ u ∗ c ~ < t > + ( 1 − Γ u ) ∗ c < t − 1 > c^{<t>} = \Gamma_u ∗ \tilde{c}^{<t>} +(1 − \Gamma_u) ∗ c^{<t−1>} c<t>=Γu∗c~<t>+(1−Γu)∗c<t−1>,记忆细胞的更新规则,门控值处于0-1之间,根据跟新公式能够有效地缓解梯度消失的问题。
- 其中, c < t > c^{<t>} c<t>、 c ~ \tilde{c} c~、 Γ u \Gamma_u Γu均具有相同的维度;
GRU的可视化实现如下图右边所示:
完整的GRU 单元:
完整的GRU单元还存在另外一个门,以决定每个时间步的候选值,公式如下:
c ~ < t > = t a n h ( W c [ Γ r ∗ c < t − 1 > , x < t > ] + b c ) Γ u = σ ( W u [ c < t − 1 > , x < t > ] + b u ) Γ r = σ ( W r [ c < t − 1 > , x < t > ] + b r ) c < t > = Γ u ∗ c ~ < t > + ( 1 − Γ u ) ∗ c < t − 1 > c < t > = a < t > \tilde{c}^{<t>} = tanh(W_c[\Gamma_r * c^{<t−1>}, x^{<t>}] + b_c) \\ \Gamma_u = \sigma(W_u[c^{<t−1>}, x^{<t>}] + b_u) \\ \Gamma_r = \sigma(W_r[c^{<t−1>}, x^{<t>}] + b_r) \\ c^{<t>} = \Gamma_u ∗ \tilde{c}^{<t>} +(1 − \Gamma_u) ∗ c^{<t−1>} \\ c^{<t>} = a^{<t>} c~<t>=tanh(Wc[Γr∗c<t−1>,x<t>]+bc)Γu=σ(Wu[c<t−1>,x<t>]+bu)Γr=σ(Wr[c<t−1>,x<t>]+br)c<t>=Γu∗c~<t>+(1−Γu)∗c<t−1>c<t>=a<t>
注:新加的 Γ r \Gamma_r Γr用于计算 c < t − 1 > c^{<t-1>} c<t−1>与next candidate for c的相关性,计算 Γ r \Gamma_r Γr需要一个新的参数矩阵 W r W_r Wr.
10. LSTM
从上述公式不难发现,GRU 与 LSTM 的一个很重要的区别点在于:
- GRU 更新与否,取决于 Γ u \Gamma_u Γu,更新的同时也意味着过去的 c < t − 1 > c^{<t-1>} c<t−1> 的遗忘与更新,而 LSTM 则不同,LSTM 一共三个门口开关: Γ u \Gamma_u Γu, Γ f \Gamma_f Γf, Γ o \Gamma_o Γo,其中更新与否看 Γ u \Gamma_u Γu,遗忘与否也是靠一个单独门口开关决定: Γ f \Gamma_f Γf。
- 其次,LSTM 的输出依旧取决于一个新的门控开关: Γ o \Gamma_o Γo,而 GRU 则一共只有两个开关: Γ u \Gamma_u Γu, Γ r \Gamma_r Γr,其输出不受控制,一定会进行输出,但是是否更新则取决于 Γ u \Gamma_u Γu,即 a < t > = c < t > a^{<t>} = c^{<t>} a<t>=c<t>;而 LSTM 则更新、遗忘、输出分别由三个门控制,其输出 a < t > = Γ O < t > ∗ c < t > a^{<t>} = \Gamma_O^{<t>} * c^{<t>} a<t>=ΓO<t>∗c<t>;
GRU能够让我们在序列中学习到更深的联系,长短期记忆(long short-term memory, LSTM)对捕捉序列中更深层次的联系要比GRU更加有效。
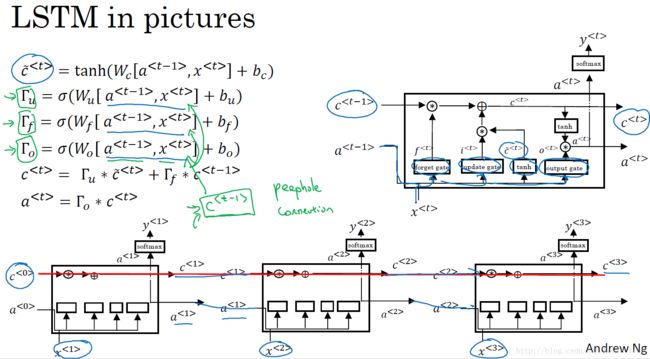
LSTM中,使用了单独的更新门 Γ u \Gamma_u Γu和遗忘门 Γ f \Gamma_f Γf,以及一个输出门 Γ o \Gamma_o Γo,其主要的公式如下:
c ~ < t > = t a n h ( W c [ a < t − 1 > , x < t > ] + b c ) Γ u = σ ( W u [ a < t − 1 > , x < t > ] + b u ) Γ f = σ ( W r [ a < t − 1 > , x < t > ] + b f ) Γ o = σ ( W o [ a < t − 1 > , x < t > ] + b o ) c < t > = Γ u ∗ c ~ < t > + Γ f ∗ c ~ < t − 1 > a < t > = Γ o ∗ c < t > \tilde{c}^{<t>} = tanh(W_c[a^{<t−1>}, x^{<t>}] + b_c) \\ \Gamma_u = \sigma(W_u[a^{<t−1>}, x^{<t>}] + b_u) \\ \Gamma_f = \sigma(W_r[a^{<t−1>}, x^{<t>}] + b_f) \\ \Gamma_o = \sigma(W_o[a^{<t−1>}, x^{<t>}] + b_o) \\ c^{<t>} = \Gamma_u ∗ \tilde{c}^{<t>} + \Gamma_f ∗ \tilde{c}^{<t-1>} \\ a^{<t>} = \Gamma_o * c^{<t>} c~<t>=tanh(Wc[a<t−1>,x<t>]+bc)Γu=σ(Wu[a<t−1>,x<t>]+bu)Γf=σ(Wr[a<t−1>,x<t>]+bf)Γo=σ(Wo[a<t−1>,x<t>]+bo)c<t>=Γu∗c~<t>+Γf∗c~<t−1>a<t>=Γo∗c<t>
LSTM单元的可视化图如下所示:
其中,在实际使用时,几个门值不仅仅取决于 a < t − 1 > a^{<t−1>} a<t−1>和 x < t > x^{<t>} x<t>,还可能会取决于上一个记忆细胞的值 c < t − 1 > c^{<t−1>} c<t−1>,这也叫做偷窥孔连接。
注:GRU与LSTM各有擅长处,LSTM具有三个门(update gate, forget gate, output gate),更加灵活,也更强大,但计算也更为复杂;而GRU则只有两个门,性能也还不错,计算消耗小,便于大规模部署;两者都有自己的适用场景,如果拿不准两者选择哪个的话建议选择LSTM。而事实上,目前也是LSTM用的更多一些。
11. 双向RNN
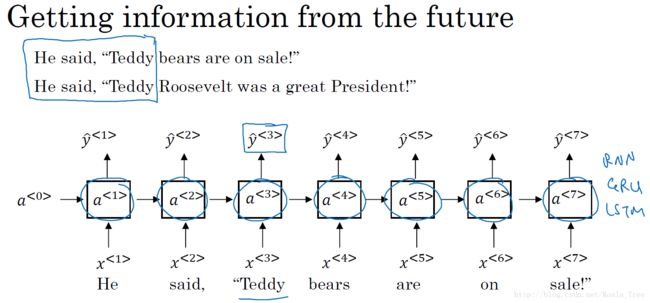
双向RNN(bidirectional RNNs)模型能够让我们在序列的某处,不仅可以获取之间的信息,还可以获取未来的信息。
对于下图的单向RNN的例子中,无论我们的RNN单元是基本的RNN单元,还是GRU,或者LSTM单元,对于例子中第三个单词”Teddy”很难判断是否是人名,仅仅使用前面的两个单词是不够的,需要后面的信息来进行判断,但是单向RNN就无法实现获取未来的信息。
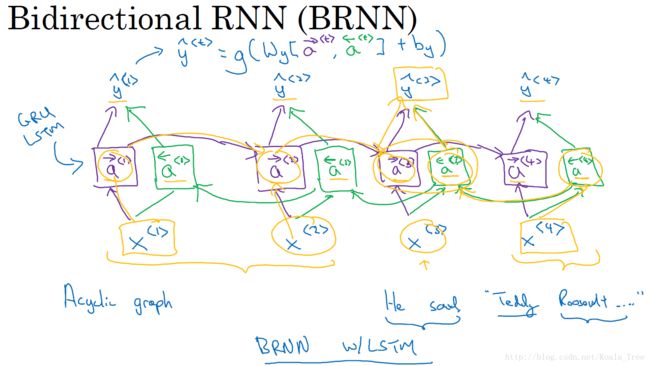
而双向RNN则可以解决单向RNN存在的弊端。在BRNN中,不仅有从左向右的前向连接层,还存在一个从右向左的反向连接层。
其中,预测输出的值 y ^ < t > = g ( W y [ a → < t > , a ← < t > ] + b y ) \hat{y}^{<t>} = g(W_y[\overrightarrow{a}^{<t>}, \overleftarrow{a}^{<t>}] + b_y) y^<t>=g(Wy[a<t>,a<t>]+by),预测结果即有前向的信息,又有反向的信息。在NLP问题中,常用的就是使用双向RNN的LSTM。
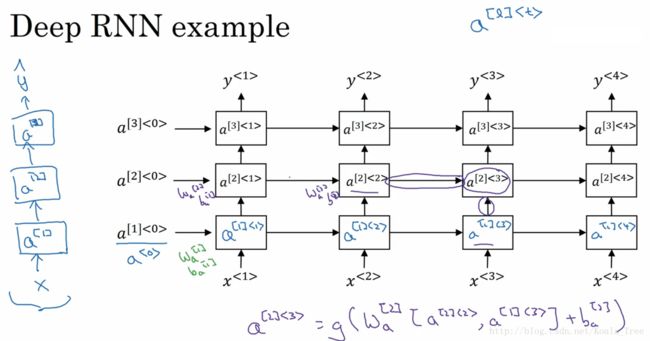
12. 深层RNNs
与深层的基本神经网络结构相似,深层RNNs模型具有多层的循环结构,但不同的是,在传统的神经网络中,我们可能会拥有很多层,几十层上百层,但是对与RNN来说,三层的网络结构就已经很多了,因为RNN存在时间的维度,所以其结构已经足够的庞大。如下图所示:
注:参考补充自:
https://blog.csdn.net/koala_tree/article/details/79299358