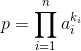学习笔记第二十节：Lucas&扩展Lucas
正题
Lucas定理大家都会：
。
long long get_C(long long x,long long y){
return (fac[x]*inv[x-y]%mod)*inv[y]%mod;
}
long long C(long long x,long long y){
if(x证明在这里就不说了，有兴趣可以翻阅其他博客。
在这里主要讲讲扩展Lucas定理，说实话个人觉得跟Lucas定理没有太大的关系。
学过那么多的“扩展”定理，就很容易推理出来扩展Lucas定理是用来解决p不为质数的情况。
首先，我们先根据唯一分解定理，把p分解为多个质数幂相乘的形式。
，其中n为不同质因子个数，ai为质数。
接着我们可以试想一下，如果我们可以求出
，用中国剩余定理合并就完事儿了。
但是我们不能直接套用Lucas定理，因为
可能不是质数。
发现：
，如果我们可以分别处理出
，那就好办了。
发现
可以分成三部分。
我们就拿
来举例。
一部分是约不了ai的，一部分是约得了ai的，把约不了ai的放在一起，约得了ai的除以ai再放在一起，放ai被除了多少次。
是不是很和谐，发现：1.n里面能被ai整除的数有
个
2.前面的数恰好在数值上分为
组（多出来的单独算），像：
，和多出来的13.
3.这组在
意义下同余
那么就很好做了，把前面的分为组，我们只需要做一组就可以知道组的答案（快速幂即可）。
中间的可以先不用算，后面的递归处理，多出来的数的个数不会超过
个（准确的来说是不超过
个），暴力处理即可。
那中间的不用算怎么处理呢？，直接用一个k暴力统计n!里面能约出来多少个
for(long long i=n;i!=0;i/=pi) k+=i/pi;
for(long long i=n-m;i!=0;i/=pi) k-=i/pi;
for(long long i=m;i!=0;i/=pi) k-=i/pi;这个是很明显的吧。
然后因为算出来的答案已经去除ai了，那么就可以直接用exgcd（或费马小定理）得出逆元求解，最后再把
呈上，就是答案了。
最后中国剩余定理合并。
void exgcd(long long a,long long b,long long&x,long long &y){
if(b==0) {x=1;y=0;return ;}
exgcd(b,a%b,y,x);
y-=a/b*x;
}
long long inv(long long a,long long b){
long long x,y;
exgcd(a,b,x,y);
x=(x%b+b)%b;
if(x==0) return b;
return x;
}
long long ksm(long long x,long long t,long long mod){
long long tot=1;
while(t>0){
if(t%2==1) (tot*=x)%=mod;
(x*=x)%=mod;
t/=2;
}
return tot;
}
long long calc(long long x,long long pi,long long pk){
if(x==0) return 1;
long long ans=1;
if(x/pk!=0){
for(int i=2;i<=pk;i++)
if(i%pi!=0) (ans*=i)%=pk;
ans=ksm(ans,x/pk,pk);
}
for(int i=2;i<=x%pk;i++) if(i%pi!=0)(ans*=i)%=pk;
return ans*calc(x/pi,pi,pk)%pk;
}
long long C(long long n,long long m,long long pi,long long pk){
long long a=calc(n,pi,pk),b=calc(n-m,pi,pk),c=calc(m,pi,pk);
long long k=0;
for(long long i=n;i!=0;i/=pi) k+=i/pi;
for(long long i=n-m;i!=0;i/=pi) k-=i/pi;
for(long long i=m;i!=0;i/=pi) k-=i/pi;
long long ans=((a*inv(b,pk)%pk)*inv(c,pk)%pk)*ksm(pi,k,pk)%pk;
ans=(ans*(p/pk)%p)*inv(p/pk,pk)%p;
return ans;
}
int main(){
scanf("%lld %lld %lld",&n,&m,&p);
long long x=p,pi,pk;
long long ans=0;
for(int i=2;i<=p;i++)
if(x%i==0){
pk=1;pi=i;
while(x%i==0) x/=i,pk*=i;
ans=((ans+C(n,m,pi,pk))%p+p)%p;
}
printf("%lld",ans);
}一直觉得这个用逆元来求中国剩余定理很妙，有兴趣的同学可以研究一下。