ALS算法原理和在音乐推荐上的应用

ALS算法原理和在音乐推荐上的应用

ALS（Alternating least squares，交替最小二乘法）本来是一种数学上的优化方法，自从有人用它在Netflix大赛中使用于推荐系统，并获得冠军后，逐渐被用在各个行业的推荐系统中。

一、ALS推荐算法的原理

1.1 矩阵分解

ALS推荐算法是基于矩阵分解的一种方法。先看矩阵分解的含义。

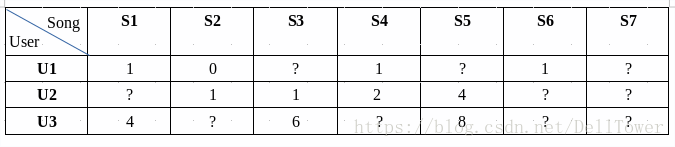
推荐所使用的数据可以抽象成一个[m,n]的矩阵R，R的每一行代表m个用户对所有歌曲的评分，n列代表每个歌曲的对应的得分。从我实际使用情况来讲，R是个“拉长”的矩阵，用户很少，歌曲很多。而且R是个稀疏矩阵，一个用户只是对所有歌曲中的一小部分听过，有评分。通过矩阵分解方法，我可以把这个低秩的矩阵，分解成两个小矩阵的点乘。公式如下：

举例如下：

评分举例如下

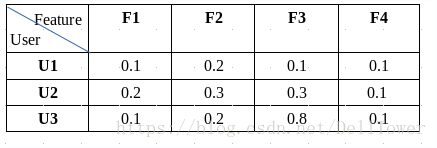
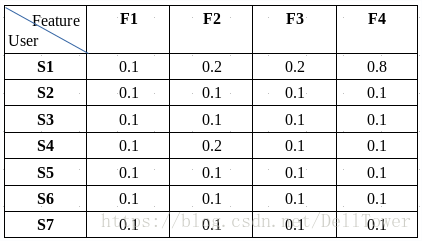
我把矩阵分解之后，就变成了下面两个小矩阵。

（用户的特征）

（歌曲的特征）

分解之后的矩阵，每个用户数据由原来的7维的向量，变成了4维的向量。这种求出的向量作为用户的特征，用在推荐上，被成为隐藏特征或者隐藏因子。

为什么进行矩阵分解呢？因为推荐使用的矩阵不仅是稀疏的而且往往是低秩的。矩阵分解相当于进行了特征提取或者数据的降维。

为了求出两个分解后的矩阵，我可以产生两个维度一样的随机矩阵U和V，点乘之后得到同样m行n列的矩阵R1. 这一步我已经得到两个[m,n]的矩阵，其中一个是反映用户的真实喜好的数据，矩阵R。另一份只是一个近似数据，矩阵R1.我可以找到一个公式来衡量，两个同阶的矩阵的相似程度：

这个函数是算法的损失函数。我的目的就是让这个函数的值最小化，使得我构造的矩阵能够最接近原始矩阵。到这一步，我的问题已经变成了一个工程优化问题，而求这个函数最小化的方法，前人已经为了我造了很多很多，比如ALS算法，梯度下降法，遗传算法，进化算法等等。

 

1.2 ALS算法

ALS是交替最小二乘法。先看下最小二乘法的含义。

假如有一些实验数据，格式是（x1,y1),（x1,y1),（x1,y1)...，

实验数据

 

然后需要求一条直线使得，这条直线能够大致经过这些点。那么求这个直线的方法就是最小二乘法，背后的数学方法就是二元函数求极值的方法。把一个变量固定，然后对另一个变量求导数后，求得极值。然后再固定另一个变量，再求得极值。我仿照最小二乘法，首先固定用户矩阵，求歌曲矩阵的极值。然后固定歌曲矩阵，求得用户矩阵的极值。交替使用这两种方法，可以得到损失函数的最小值。

ALS算法的实现可以在这篇博客（http://blog.ethanrosenthal.com/2016/01/09/explicit-matrix-factorization-sgd-als/）找到。略去前面的数据处理不提，看完他的代码后可以总结出他的实现方法。

 

假设评分矩阵的阶是[m,n]，代表有m个用户，n首歌曲，假设求出的两个小矩阵中隐藏因子是40个。

1、训练的时候，首先生成两个随机矩阵，一个是用户的，一个是歌曲的，列数就是隐形因子的个数。

   self.user_vecs = np.random.random((self.n_users, self.n_factors))
   self.item_vecs = np.random.random((self.n_items, self.n_factors))
（train函数中生成随机矩阵的代码）

这两个随机矩阵就是我想要的分解矩阵，但是它们的值都是随机数，可能不是让我的损失函数取最小值的矩阵，我还要进行训练，改变两个矩阵的值。

 

2、然后用上次生成的矩阵拟合真正的评分矩阵，实施训练的是als_step这个函数

self.user_vecs = self.als_step(self.user_vecs, 
                                           self.item_vecs, 
                                           self.ratings, 
                                           self.user_reg, 
                                           type='user') = self.als_step(self.user_vecs, 
                                           self.item_vecs, 
                                           self.ratings, 
                                           self.user_reg, 
                                           type='user')

（训练用户矩阵的代码）

用交替最小二乘法求损失函数的最小值时，先固定歌曲的矩阵，让它的值不变，这样我的损失函数中只有用户矩阵在变化，我先求出歌曲矩阵不变时，让损失函数取最小值时的用户矩阵。

 

3、训练用户矩阵

   if type == 'user':
            # Precompute
            YTY = fixed_vecs.T.dot(fixed_vecs)
            lambdaI = np.eye(YTY.shape[0]) * _lambda

            for u in xrange(latent_vectors.shape[0]):
                latent_vectors[u, :] = solve((YTY + lambdaI), 
                                             ratings[u, :].dot(fixed_vecs))
            # Precompute
            YTY = fixed_vecs.T.dot(fixed_vecs)
            lambdaI = np.eye(YTY.shape[0]) * _lambda

            for u in xrange(latent_vectors.shape[0]):
                latent_vectors[u, :] = solve((YTY + lambdaI), 
                                             ratings[u, :].dot(fixed_vecs))

（训练代码）

 

首先，这个latent_vectors是用户矩阵，shape是[m, 40]，fixed_vecs矩阵就是歌曲矩阵，shape是[n,40]。歌曲矩阵点乘其专置矩阵得到矩阵YTY，shape是[n,n]。

然后，产生一个值是_lambda的对角矩阵，shape是[n,n]，_lambda是个参数范围是[0,1]。

最后，循环每个用户矩阵的每个用户，得到其打分矩阵latent_vectors[u,:]，shape是[m,40]。

下面就是一个解线性方程组的过程了。系数矩阵是 YTY + lambdaI,常数矩阵是用户u 的评分矩阵 a（shape是 [1,n]）， 点乘歌曲矩阵 b（shape 是[n, 40]）， 得到矩阵 c（shape是[1,40]），这个过程类似于降维。点乘的几何意义是可以用来表征或计算两个向量之间的夹角，以及在b向量在a向量方向上的投影。我将歌曲表征为40维的向量，即为原来的评分向量在40维这个向量上的投影。解出方差组，解是40列的向量，赋值给用户矩阵中对应用户的随机值。

 

4、接着训练歌曲矩阵，步骤类似，代码如下。

 elif type == 'item':
            # Precompute
            XTX = fixed_vecs.T.dot(fixed_vecs)
            lambdaI = np.eye(XTX.shape[0]) * _lambda
 
            for i in xrange(latent_vectors.shape[0]):
                latent_vectors[i, :] = solve((XTX + lambdaI), 
                                             ratings[:, i].T.dot(fixed_vecs))
            # Precompute
            XTX = fixed_vecs.T.dot(fixed_vecs)
            lambdaI = np.eye(XTX.shape[0]) * _lambda
 
            for i in xrange(latent_vectors.shape[0]):
                latent_vectors[i, :] = solve((XTX + lambdaI), 
                                             ratings[:, i].T.dot(fixed_vecs))

（训练歌曲矩阵的代码）

5、循环进行步骤3和步骤4，总共训练7轮，每轮训练的次数是 1， 3，5，...，每训练一次使用一次交替二乘法。相当于训练len(iter_array)轮，每轮训练的次数逐渐增多

     for (i, n_iter) in enumerate(iter_array):
            if self._v:
                print 'Iteration: {}'.format(n_iter)
            if i == 0:
                self.train(n_iter - iter_diff)
            else:
                self.partial_train(n_iter - iter_diff)

            predictions = self.predict_all()

            self.train_mse += [get_mse(predictions, self.ratings)]
            self.test_mse += [get_mse(predictions, test)]
            if self._v:
                print 'Iteration: {}'.format(n_iter)
            if i == 0:
                self.train(n_iter - iter_diff)
            else:
                self.partial_train(n_iter - iter_diff)

            predictions = self.predict_all()

            self.train_mse += [get_mse(predictions, self.ratings)]
            self.test_mse += [get_mse(predictions, test)]

6、训练结束后，求预测值，得到预测矩阵，然后计算预测矩阵和真实评分矩阵的差异，就是代码中get_mse函数。

经过调试参数后，我得到了最终的两个分解矩阵，这两个分解矩阵就可以用在推荐系统中。

 

二、ALS推荐算法的应用

我的目的是利用ALS算法做歌曲推荐。为了达到这个目的，可以使用下面的流程。

1、接收给用户歌曲推荐的请求。

2、获取用户的历史记录（包括用户听歌历史、收藏的歌曲、分享的歌曲）。

3、根据历史记录中的歌曲获取相似歌曲。

4、权重排序。

5、返回结果。

ALS算法可以用在第三步，求相似歌曲上面。当训练结束后，得到了歌曲的矩阵，shape是[m,40]。可以两两计算余弦相似度，就可以得到某首歌曲的相似歌曲。

总结一下，我利用用户的听歌记录，训练ALS算法，得到歌曲的隐藏因子表达，然后计算相似歌曲，用来做音乐推荐。

当然，实际运用时我还没有能力像这篇博客的作者一样完整、准确地写出ALS的算法，而是调用Spark的库。而且还要考虑长尾效应、无效歌曲、无效用户等问题。但是原理我还是要搞懂的。