期望与概率

预备知识

定义
P（A） ：事件A发生的概率；
E（A） ：事件A的期望。
对于离散的事件 A1，A2，A3...An ，则定义其期望为 P（A）×A ，这里可以推出，若概率为 P（A） ，设此概率为 pq ，则不妨设样本容量为 q ，则其发生次数为 p ，从而其期望为 A×pq ，若其样本为等地位的，则其期望中 A 可以省去，故有： E（A）=1P(A) 。
从而可以以其解题。

题目

bzoj 1426

          有n种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买，每次只能买一张，并且买到的邮票究竟是n种邮票中的哪一种是等概率的，概率均为1/n。但是由于凡凡也很喜欢邮票，所以皮皮购买第k张邮票需要支付k元钱。 现在皮皮手中没有邮票，皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。

首先，我们先做一个入门版本的此题：
有 n 种不同的邮票，皮皮想收集所有种类的邮票。唯一的收集方法是到同学凡凡那里购买，每次只能买一张，并且买到的邮票究竟是n种邮票中的哪一种是等概率的，概率均为 1n 。现在皮皮手中没有邮票，皮皮想知道自己得到所有种类的邮票需要花费的钱数目的期望。
我们假设 f(i) 为 已经有了 i 种,接着买完剩下 （n−i） 种的期望，那么明显有
f（i）=n−in×f(i+1)+in×f(i)+1 ;即化简得 f(i)=f(i+1)+n−in 。
为什么呢？这是因为当我们买下一张票的时候，有的概率买到新的一种，有概率买到原有的，而由于已经买了一张新的，那么买一张的新的概率就为1，所以由期望的公式得，要加上 1 ，有些题解说还要记录一个 g（i） 数组表示得到i种的概率，实际上没必要。原因马上讲。注意之前的定理，有 E（A）=1P(A) ，条件是事件地位平等，我们不妨这样，买一张买到一张新的概率是 n−in 那么由公式得其期望为 n−in ，那么有全期望公式可得， f(i)=f(i+1)+n−in ，与之前一模一样。

所以正解是
我们可以得到，对于这个 g ，实际上是等概率的(都是一个收敛的级数，分布均匀),所以不用记录 g 数组。而且，我们也更加可得 E（A）=1P(A) 的重要性与巧妙性了。
好了，回到这道题，注意到每张邮票买的钱不一样，那么，我们可以理解为当概率相同时，权值不一样，所以期望不一样。所以也可以看成当权值相同时，概率不一样，所以这次要记录一个 g 表示还要多少钱，当然也可以记概率，但更复杂。所以用 f[i] 表示已经拥有了 i 张邮票，则期望还需要购买的邮票数。
f[i]=f[i]×in+f[i+1]×n−in+1
f[i]=f[i+1]+nn−i;
又有
g[i]=n−in×(g[i+1]+f[i+1])+in×(g[i]+f[i])+1
化简得
g[i]=g[i+1]+f[i+1]+n×i(n−i)×n×f[i]+nn−i 。
然后，就两个数组一起搞啊~~~。
（权限题，所以我也不确定正不正确，如果想要，找其他人吧。）

bzoj4832

（好题，以后玩炉石可以用）。题意是告诉你克苏恩的攻击力，你场上的随从状态（只有奴隶主，可能一血，二血，三血），问你克苏恩对英雄的伤害的期望。
题解
记录 dp[i][m][n][k] 表示克苏恩i点攻击力， 1—3 血分别有 m,n,k 个时，把攻击打完受到的伤害（最好不要倒着定义成现在到打完还要受多少，时间会多一个常数）。然后，概率 dp 转一转就好了。注意这里的概率的分母为 1+m+n+k ，因为还有个英雄。而且要注意，有可能造不出奴隶主了。（好题）
代码如下

#include
#include
using namespace std;
int i,m,n,k;
double dp[70][10][10][10];//已经受了这么多伤[m][n][k] m 1,n 2,k 3 
int main()
{

    for (int i = 1; i<=50 ;i++)
       for (int m = 0;m <= 7;m++)
        for (int n = 0; n <= 7 - m;n++)
          for (int k = 0;k  <= 7 - m - n ;k++)
          {
            int j = m + n + k;
            double seg = 1.0 / (m + n + k + 1.0);
            dp[i][m][n][k] += seg * ( dp[i-1][m][n][k] + 1.0);
            if (m) dp[i][m][n][k] +=  (double)m * seg * dp[i-1][m-1][n][k];
            if (n)
            {
                if (j<7) dp[i][m][n][k] += seg * (double)n * dp[i-1][m+1][n-1][k+1];
                else dp[i][m][n][k] += seg * (double)n * dp[i-1][m+1][n-1][k];
            }
            if (k)
            {
                if (j<7) dp[i][m][n][k] += seg * (double)k * dp[i-1][m][n+1][k];
                else dp[i][m][n][k] += seg * (double)k * dp[i-1][m][n+1][k-1];
            }
        }   
    int t;scanf("%d",&t);    
    while (t--)
    {

        scanf("%d%d%d%d",&i,&m,&n,&k);
        printf("%.2lf\n",dp[i][m][n][k]);
    }

    return 0;
 } 

bzoj 1419

翻钱，给定红钱个数，黑钱个数，一个一个翻，但是你只能知道还剩几个红，几个黑，翻到红就 +1s ，黑就 −1s ，可以随时不翻，然后就算成一种情况，求在最优策略下的期望。
题解
首先，最优策略明显就是当剩下的钱黑的多就不翻了,然后，就没别的策略了，拼 RP 了。设 dp[i][j] 为剩下 i 个红色， j 个黑色的期望，转移就是一般的转移，但是注意，我们得从后推 dp ，因为从前推我们不一定能推到最优策略（想想我们的最优策略，是看之后还要怎么翻，而明显，从后推时， dp[1][1] ， dp[1][0] 这些我们都可以直接推出，所以从后推（我是指相对答案从后推，答案是 dp[imax][jmax] ））。（还是水）。
代码如下(权限题，错了不怪我，我也没试过)

#include
#include
#include
using namespace std;
double dp[3][5010];
int r,b;
double k;
int main()
{
    scanf("%d%d",&r,&b);
    for (int i = 1;i <= r;i++)
    {
        dp[i%2][0] = i;
        for (int j = 1 ;j <= b;j++)
        {
        double A = (double)i/(i+j),B = (double)j/(i+j);
        k = A * ( dp[ (i-1)%2 ][j] + 1) + B* ( dp[i%2][j-1] -1);
        dp[i%2][j] = max(0.0, k);
        }
    }
    dp[r%2][b]=floor(dp[r%2][b]*=100000);
    dp[r%2][b]/=1000000;
    printf("%.6lf",dp[r%2][b]);
    return 0;
}

bzoj1415

（题太长了，自己去看吧……）
题解
组合题，但实际上并不难，只需要首先用 bfs 搜一遍路径，用 x[i][j] 表示从 i 走到 j 下一步的点，由于要去最小的，所以还要记一个 dis 数组，然后判定距离加打擂台确定 x[i][j] 的值,接着就简单了，简单的期望 dp 转移，但是还要加上那只耗子不动的可能。 dp 的时候，由于是图上 dp ，最好写一个记忆化搜索，当然大佬可以写其他方法（膜）。（没那么水）（汤姆表示自己也想要一个这样的 GPS ）。
代码如下：

#define f(x,y,z) for (int x=(y);x<=(z);x++)
#include
#include
#include
#include
#include
using namespace std;
const int maxn =1005;
struct Edge{
    int fr,to,next;
}edge[maxn*2];int line_cnt=0;
int head[maxn] , val[maxn]; int head_cnt = 0;
int x[maxn][maxn],dis[maxn][maxn];
double f[maxn][maxn];
int n,e;
int mou,cat;
void addedge(int f,int t)
{
    int a = head[f];
    edge[++line_cnt] = (Edge){f,t,a} ;
    head [f] = line_cnt;
}
void adde(int f,int t)
{
    addedge(f,t);
    addedge(t,f);
}
void bfs(int start)//要记录距离
{
    queue<int> q;
    dis[start][start] =0;
    q.push(start);
        while (!q.empty())
    {
        int r = q.front();q.pop();int tmp = x[start][r];
        for (int i = head[r]; i ;i = edge[i].next)
        {
            int u = edge[i].to;
            if (dis [start][u]==-1 || (dis[start][r] +1 == dis[start][u] && tmp < x[start][u]))    
            {
            dis[start][u] = dis[start][r] +1;
            if (tmp) x[start][u] = tmp;else x[start][u] = u;
            q.push(u);
            }
        }
    }
}
double dp(int cc,int kk)//记忆化搜索
{
    int n1 = x[cc][kk];
    int n2 = x[n1][kk]; 
    if (f[cc][kk] != -1) return f[cc][kk];
    if (cc == kk) return f[cc][kk] = 0;
    if (n1  == kk) return f[ cc ][kk] = 1;
    if (n2 == kk) return f[ cc ][kk] = 1;
    f[cc][kk] = 0;
    for (int i = head[kk]; i ;i = edge[i].next)
    {
        int u = edge[i].to;
        f[cc][kk] += dp(  n2 , u );
    }
    f[cc][kk] = ( f[cc][kk] + dp( n2 , kk) ) / (double) ( val[kk] + 1 ) +1;
    return f[cc][kk];
}

int main()
{
    scanf("%d%d",&n,&e);
    scanf("%d%d",&cat,&mou);
    int ua,ub;
    memset(dis,-1,sizeof dis);
    memset(val,0,sizeof val);
    for (int i = 1;i<=n;i++)
      for (int j = 1;j<=n;j++)
         f[i][j]=-1;
    for (int i=1;i<=e;i++)
    {
        scanf("%d%d",&ua,&ub);
        val[ua]++;val[ub]++;
        adde( ua , ub);
    }
    for (int i = 1 ;i<=n;i++) {bfs(i);x[i][i]=i;}
    printf("%.3lf", dp(cat , mou));
    return 0;
}

树上期望：

• 树上随机游走的期望（求从根节点第一次到其他节点的期望步数）：

由期望的可加性，有从 root 到 i 的期望等于 root 到 i 的父亲 fa 的期望加上 fa 到 i 的期望，明显 root 到 fa 的期望就变成了一个递归的问题，从而只需求出 fa 到 i 的期望就行了。
d[i] 表示 i 的度数，每条边的长度均为1。 F[i] 表示从 i 走到其父亲的期望步数， G[i] 表示从 i 的父亲 fa 走到 i 的期望，所以有对于 F[i] ，则有如下可能：直接走到父亲，走到i的某一个儿子又走回来又走到父亲，即有 F[i]=(1+∑F[son]+1+F[i])d[i] ，化简得
F[i]=d[i]+∑F[son] （因为 i 的儿子有 d[i]−1 那么多个）

接着看 G[i] ，我们有从 fa 走到一个错误的儿子，走到 fa 的父亲，走到 i 这三种情况。
G[i]=1+G[fa]+G[i]+1+∑F[brother]+G[i]+1d[fa] ，
化简得
G[i]=G[fa]+d[fa]+∑F[brother] 。
即：
F[fa]−F[i]=d[fa]+∑F[brother] 。
G[i]=G[fa]+F[fa]−F[i] 。

• 更简单的方法：

上面的实际上就足够了，复杂度是 O（n） 的，常数为 2 （两遍 dfs ），但是还有更好的，一边 dfs 就可以搞定，而且更简单。
不仿设第 i 个点的期望是 ans[i] ，那么有 ans[i]=ans[fa]+G[i] （ G[i] 就是之前的东西）。
那么这个 G[i] 由之前的式子可得
G[i]=G[fa]+d[fa]+∑F[brother]
， G[fa] 又是什么呢？
再迭代可得
G[fa]=G[grandfa]+d[grandfa]+∑F[brother] 。
如此下去，直到 root，G[root]=0 ，将这些式子加起来，可得
G[i]=∑d[ancester]（除了i）+∑∑F[brother] （这个双segma表示的是对于每一个 ancester 而言，其除了 i 的祖先的儿子的 F 之和）。
注意到
F[j]=d[j]+∑F[son]
，那么对于一个 F[j] ，我们递归可以得到
F[j]=以j为根的子树的度数总和+1 （加一是因为i还有一个特殊的度是通向其父亲的）
，那么这个 f[j]+d[j] 不就是这个树的度数 +1 。
又因为其度数中，一条边算了两次（除了j通向其父亲的），所以这棵树的度数= 2× 其点数 −1 （不忘特殊边只算过一次），所以这个式子是以 j 为根的的子树的大小，出了 j 走向 i 的那颗子树，所以求和之和是长这样的：

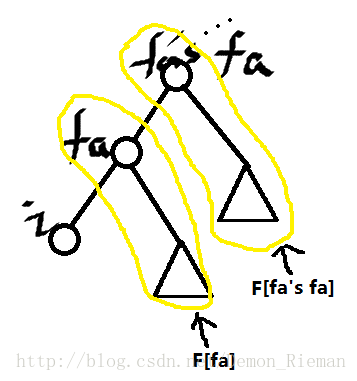
蛤？那不就是除了 i 以外的树的大小的两倍？但是我们还是要注意，根节点没有头上的那根，所以还要减一，所以将每个 ∑F[son]与d[ancester] 匹配，我们得到了：
G[i]=2（n−Size[i]）+1 。

从而 ans[i]=ans[fa]+2(n−size[i])+1 。那这个就可以一遍搞定了。

• 另解：

对于这个式子证明还有一个感性的理解，因为我们想， G[i] 而言，从 fa 走到 i 的期望，我们不管什么树，什么路径，我们这样想，从 n 个节点中随便选一个，如果选到 i 及其子树上的点，那么肯定走到过 i ，反之，就没走到过，所以选到其子树概率是 sizen ，又因为概率等于期望的倒数，所以有 G[i]=2（n−size[i]）+1 。（乱证的，请自行跳过。）

连续样本的期望

作为一个数竞党，再发一个对连续样本期望的求法（实际上就是积分一下就好了）（转自百度百科）：

最后要说的

好吧，最后说一下，这是我的第一篇博客，其中一些想法借鉴了许多大犇的题解，所以如果发现有雷同，那很可能是我从前看过的，然后整理了一下吧……