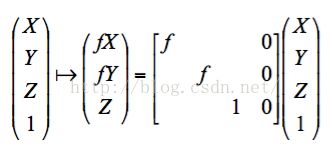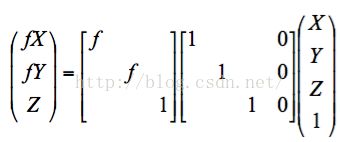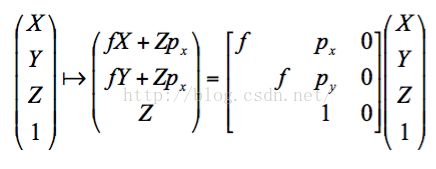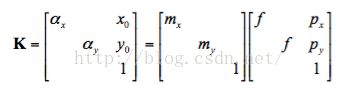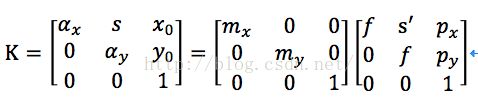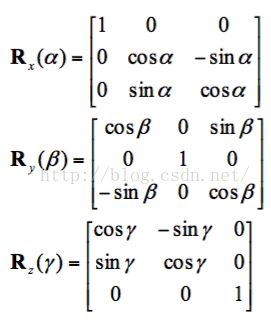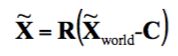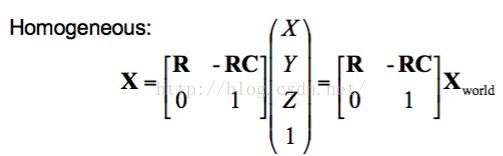三维重建学习（二）相机的标定（上）

前言

这一篇主要补充一些关于三维重建的数学理论和模型，因为想理解相机的标定需要有一定的理论基础。相机标定的具体方法以及数学表达在下一篇具体讲解。

Homogeneous Coordinate 齐次坐标

齐次坐标与我们一般使用的笛卡尔坐标（下文统一用非齐次坐标代称）有一个本质的区别，就是齐次坐标多了一个component，具体来说，在三维世界中，非齐次坐标用（x, y, z）来刻画一个点的位置。而齐次坐标则是(x, y, z, 1)或者更一般化的(x, y, z, w)。

显然最大的疑惑是为什么要引入齐次坐标？或者说用齐次坐标刻画三维世界有什么独特的好处？齐次坐标最大的特点叫做 “Invariant to scaling”.简单来说，齐次坐标对于乘以或者除去一个常量的运算可以保持不变。为什么是这样？这个问题我先不回答，接下来讲完齐次坐标与非齐次坐标的转换后，答案自然就明了了。

Inhomogeneous to Homogeneous

将一个点从非齐次坐标转换成齐次坐标很简单，而且是绝对的。

例如点 (x, y, z, w) ，首先要将其最后一个量化成1，即（x/w, y/w, z/w, 1），然后取前三个量即可得到对应的齐次坐标。从这就很容易理解，为什么非齐次坐标乘以一个标量后，并没有实际意义，因为其实际对应的齐次坐标点并没有发生改变。

Homogeneous to Inhomogeneous

把一个点从齐次坐标转换到非齐次坐标中，默认到方法就是在原坐标中再加一个1，即 (x, y, z) 变成了 (x, y, z, 1)。但事实是这不是一个单一解的绝对过程，从上面的转换也可以看出，非齐次坐标中的一个点对应齐次坐标中的唯一一个点，但是反之却并不唯一。点（x，y，z）可以对应由任何实数w构成的点（wx，wy，wz，w）。

Camera Model 相机模型

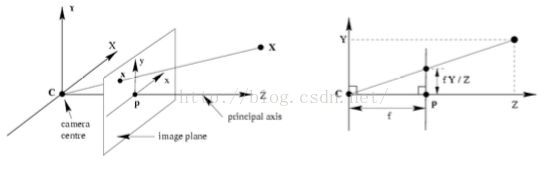
Pinhole Camera Model 小孔成像

根据相似三角形，可以表达出空间中的点X与原点C的连线最终交与投影平面的点的3D坐标

想拿到这个3D点在2D平面上的坐标，只要把Z轴的量舍去即可

Intrinsic Matrix 内部矩阵

以上便是在非齐次坐标中3D点与其对应的2D点的坐标，但是实际的表达是要用齐次坐标来完成，所以要将两个点都化为齐次坐标

将这个运算用矩阵表达，很容易能得到上图的矩阵，这个矩阵便是Camera Matrix（相机矩阵），通常用字母P来表示。但这个形式不是我们常用的表达形式，还可以对其做进一步的分解

最后得到的这个矩阵由两部分组成，左边3x3的矩阵叫做Intrinsic Matrix，用字母K表示，主要包含相机的内部信息，比如f便是焦距，这些信息是给定的相机后就确定的，不依赖于外界环境的。右边3x4的矩阵叫做Extrinsic Matrix，主要包含的是外部信息，是独立于相机本身参数的。这个矩阵主要由两部分组成，即Rotational Matrix（旋转矩阵）和Translational Vector（平移向量），下图的表示方法更清晰一些

这里的单位矩阵I代表的便是旋转矩阵，用R表示，而零向量0则表示平移向量，用t表示。一组R和t的参数共同构成了相机的Relative Pose（相对位置），这个概念先提出来，以后再解释。不难发现这里R＝I，而t＝0，代表的是一个参考，因为只有一个相机，相对于它本身而言显然是不需要旋转和平移的。

Projective Camera Model 投影相机

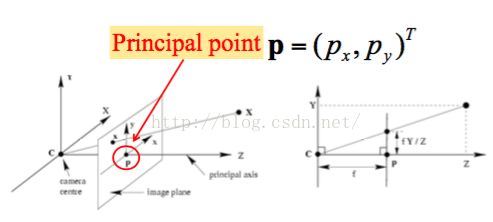
这个模型是基于小孔成像模型的，在其基础上增加了Pricipal Point（主点）的概念。投影平面与Pricipal Axis（主轴）的交点并不一定就是投影平面的原点，所以Principal Point的坐标并不一定是（0，0），这里用一个列向量  p 来表示其坐标

有了这一改变后，对应的相机矩阵也会有所变化

显然，其对应的x和y坐标在小孔成像模型中是0，所以小孔成像模型中的Intrinsic Matrix是一个Diagonal Matrix（对角矩阵），但是一般化的模型中，应该是一个Upper Triangular Matrix（上三角矩阵）。

CCD Camera Model  以CCD为传感器的相机

若是考虑传感器的因素，可以发现，传感器在横向与纵向的单位像素长度并不一定相等，所以以上所有模型在考虑到相机的内部结构时，都要乘一个单位像素长度，用m来表示。这样的结果就是Intrinsic Matrix即矩阵K会发生一些微小的变化

除此之外，矩阵K还有另一个参数，叫做Skew Factor，用字母s表示，但但多数情况都为零，在此不赘述

Extrinsic Matrix 外部矩阵

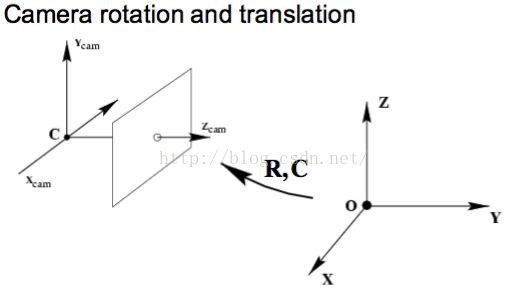
以上都是关于Intrinsic Matrix，接下来是关于Extrinsic Matrix的信息，当涉及Extrinsic Matrix的时候，就要涉及到两个不同的相机矩阵

从这个图中大致可以看出两个不同的相机位置之间的关系

首先提一下空间中的旋转，这可以理解为分别绕x，y，z轴旋转角度a，b，c

最终的矩阵R可以表示为这三个矩阵的乘积

回归正题，以上图为例，若取左上角的相机作为参考，那么它对应的Extrinsic Matrix 便是很简单的［ I｜0 ］，问题在于如何拿到位于右下角这个相机对应的外部矩阵。可以这样想，投影方程 x＝PX，刻画的是一个空间中的点与其对应的平面中的点的关系，既然已知了参考坐标下的相机矩阵也就是P，那么只要做一个的空间坐标变换，便可找到第二个坐标系对应的相机矩阵。

C表示参考坐标系的原点在第二个坐标系中的空间坐标，这里用其负值表示一个反向平移的关系。Xworld表示的是同一个三维点在第二个坐标系中对应的空间坐标，X代表参考系中的空间坐标，波浪线表示这是在非齐次坐标下，也就是说一个坐标只有3个量。

但事实是我们的相机矩阵都是在齐次坐标下刻画出来的，所以这里需要用齐次坐标来重新表达这个关系。

上图便是齐次坐标中关于坐标转换的表达，接下来直接将变换后的空间坐标X代入参考坐标系下的投影方程，便可以得到第二个坐标系中的投影方程

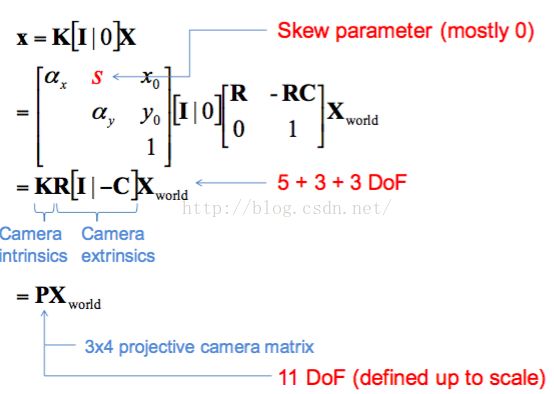
以上便是最一般化的投影方程

关于相机的标定，实际上就是确定相机矩阵P，或者有时只需要内部矩阵K即可，因为外部矩阵并不是绝对的。

关于相机矩阵P，这是一个3x4的矩阵，一共12个量，但是它的自由度只有11。这是因为相机矩阵P是在齐次坐标的表达下求解出来的，由于齐次坐标存在Scaling Ambiguity，我们无法确定乘的这个标量，所以相机矩阵也存在相同的问题，这使得它失去了一个自由度。

更具体来说，在内部矩阵K中有5个自由度，分别是那5个参数，旋转矩阵有3个自由度，分别是绕x，y，z旋转的三个角度，平移向量有三个自由度，分别是点C在非齐次坐标下的三个坐标值。

－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－－

以上是所有需要的理论基础，下一篇会讲解具体的相机标定实现方法。