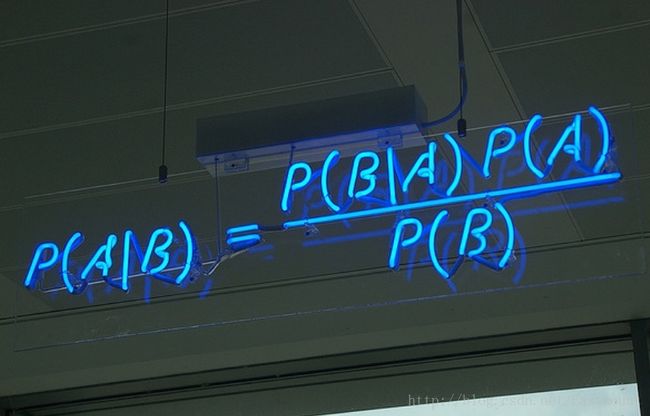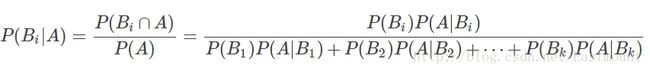【python数据挖掘课程】二十一.朴素贝叶斯分类器详解及中文文本舆情分析
1.朴素贝叶斯数学原理知识
2.naive_bayes用法及简单案例
3.中文文本数据集预处理
4.朴素贝叶斯中文文本舆情分析
本篇文章为基础性文章，希望对你有所帮助，如果文章中存在错误或不足之处，还请海涵。同时，推荐大家阅读我以前的文章了解基础知识。
前文参考：
【Python数据挖掘课程】一.安装Python及爬虫入门介绍
【Python数据挖掘课程】二.Kmeans聚类数据分析及Anaconda介绍
【Python数据挖掘课程】三.Kmeans聚类代码实现、作业及优化
【Python数据挖掘课程】四.决策树DTC数据分析及鸢尾数据集分析
【Python数据挖掘课程】五.线性回归知识及预测糖尿病实例
【Python数据挖掘课程】六.Numpy、Pandas和Matplotlib包基础知识
【Python数据挖掘课程】七.PCA降维操作及subplot子图绘制
【Python数据挖掘课程】八.关联规则挖掘及Apriori实现购物推荐
【Python数据挖掘课程】九.回归模型LinearRegression简单分析氧化物数据
【python数据挖掘课程】十.Pandas、Matplotlib、PCA绘图实用代码补充
【python数据挖掘课程】十一.Pandas、Matplotlib结合SQL语句可视化分析
【python数据挖掘课程】十二.Pandas、Matplotlib结合SQL语句对比图分析
【python数据挖掘课程】十三.WordCloud词云配置过程及词频分析
【python数据挖掘课程】十四.Scipy调用curve_fit实现曲线拟合
【python数据挖掘课程】十五.Matplotlib调用imshow()函数绘制热图
【python数据挖掘课程】十六.逻辑回归LogisticRegression分析鸢尾花数据
【python数据挖掘课程】十七.社交网络Networkx库分析人物关系（初识篇）
【python数据挖掘课程】十八.线性回归及多项式回归分析四个案例分享
【python数据挖掘课程】十九.鸢尾花数据集可视化、线性回归、决策树花样分析
【python数据挖掘课程】二十.KNN最近邻分类算法分析详解及平衡秤TXT数据集读取
一. 朴素贝叶斯数学原理知识
该基础知识部分引用文章"机器学习之朴素贝叶斯(NB)分类算法与Python实现"，也强烈推荐大家阅读博主moxigandashu的文章，写得很好。同时作者也结合概率论讲解，提升下自己较差的数学。
朴素贝叶斯（Naive Bayesian）是基于贝叶斯定理和特征条件独立假设的分类方法，它通过特征计算分类的概率，选取概率大的情况，是基于概率论的一种机器学习分类（监督学习）方法，被广泛应用于情感分类领域的分类器。
下面简单回顾下概率论知识：
1.什么是基于概率论的方法？
通过概率来衡量事件发生的可能性。概率论和统计学是两个相反的概念，统计学是抽取部分样本统计来估算总体情况，而概率论是通过总体情况来估计单个事件或部分事情的发生情况。概率论需要已知数据去预测未知的事件。
例如，我们看到天气乌云密布，电闪雷鸣并阵阵狂风，在这样的天气特征(F)下，我们推断下雨的概率比不下雨的概率大，也就是p(下雨)>p(不下雨)，所以认为待会儿会下雨，这个从经验上看对概率进行判断。而气象局通过多年长期积累的数据，经过计算，今天下雨的概率p(下雨)=85%、p(不下雨)=15%，同样的 p(下雨)>p(不下雨)，因此今天的天气预报肯定预报下雨。这是通过一定的方法计算概率从而对下雨事件进行判断。
2.条件概率
若Ω是全集，A、B是其中的事件（子集），P表示事件发生的概率，则条件概率表示某个事件发生时另一个事件发生的概率。假设事件B发生后事件A发生的概率为：
设P(A)>0，则有 P(AB) = P(B|A)P(A) = P(A|B)P(B)。
设A、B、C为事件，且P(AB)>0，则有 P(ABC) = P(A)P(B|A)P(C|AB)。
现在A和B是两个相互独立的事件，其相交概率为 P(A∩B) = P(A)P(B)。
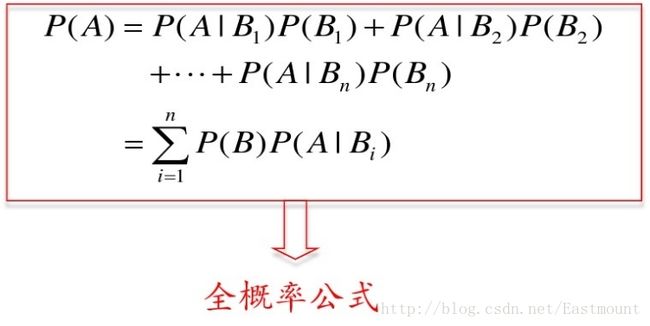
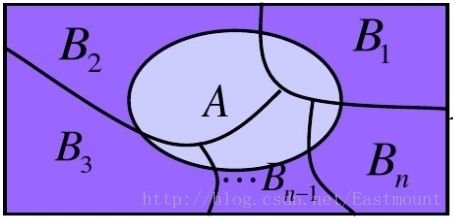
3.全概率公式
设Ω为试验E的样本空间，A为E的事件，B1、B2、....、Bn为Ω的一个划分，且P(Bi)>0，其中i=1,2,...,n，则：
= P(A|B1)P(B1)+P(A|B2)P(B2)+...+P(A|Bn)P(Bn)
示例：有一批同一型号的产品，已知其中由一厂生成的占30%，二厂生成的占50%，三长生成的占20%，又知这三个厂的产品次品概率分别为2%、1%、1%，问这批产品中任取一件是次品的概率是多少？
4.贝叶斯公式
设 Ω为试验E的样本空间，A为E的事件，如果有k个互斥且有穷个事件，即B1、B2、....、Bk为Ω的一个划分，且P(B1)+P(B2)+...+P(Bk)=1，P(Bi)>0（i=1,2,...,k)，则：
P(A∩B)：事件A和事件B同时发生的概率；
P(A|B)：事件A在时间B发生的条件下发生的概率；
意义：现在已知时间A确实已经发生，若要估计它是由原因Bi所导致的概率，则可用Bayes公式求出。
5.先验概率和后验概率
先验概率是由以往的数据分析得到的概率，泛指一类事物发生的概率，根据历史资料或主观判断未经证实所确定的概率。后验概率而是在得到信息之后再重新加以修正的概率，是某个特定条件下一个具体事物发生的概率。
6.朴素贝叶斯分类
贝叶斯分类器通过预测一个对象属于某个类别的概率，再预测其类别，是基于贝叶斯定理而构成出来的。在处理大规模数据集时，贝叶斯分类器表现出较高的分类准确性。
假设存在两种分类：
1) 如果p1(x,y)>p2(x,y)，那么分入类别1
2) 如果p1(x,y)
1) 如果p(c1|x,y)>p(c2,|x,y)，那么分类应当属于类别c1
2) 如果p(c1|x,y)
贝叶斯定理最大的好处是可以用已知的概率去计算未知的概率，而如果仅仅是为了比较p(ci|x,y)和p(cj|x,y)的大小，只需要已知两个概率即可，分母相同，比较p(x,y|ci)p(ci)和p(x,y|cj)p(cj)即可。
7.示例讲解
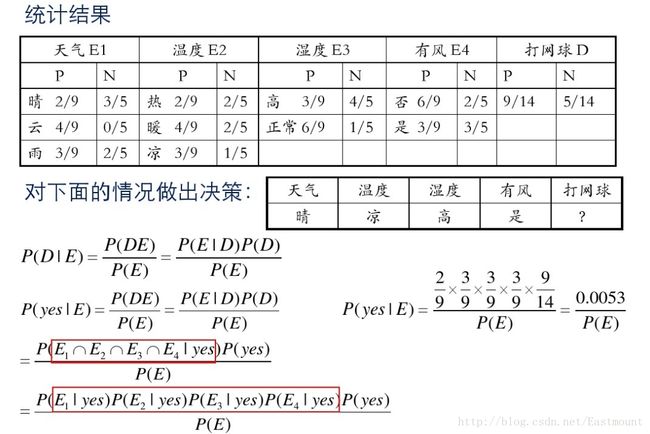
假设存在14天的天气情况和是否能打网球，包括天气、气温、湿度、风等，现在给出新的一天天气情况，需要判断我们这一天可以打网球吗？首先统计出各种天气情况下打网球的概率，如下图所示。
8.优缺点
- 监督学习，需要确定分类的目标
- 对缺失数据不敏感，在数据较少的情况下依然可以使用该方法
- 可以处理多个类别 的分类问题
- 适用于标称型数据
- 对输入数据的形势比较敏感
- 由于用先验数据去预测分类，因此存在误差
二. naive_bayes用法及简单案例
scikit-learn机器学习包提供了3个朴素贝叶斯分类算法：
- GaussianNB(高斯朴素贝叶斯)
- MultinomialNB(多项式朴素贝叶斯)
- BernoulliNB(伯努利朴素贝叶斯)
1.高斯朴素贝叶斯
调用方法为：sklearn.naive_bayes.GaussianNB(priors=None)。
下面随机生成六个坐标点，其中x坐标和y坐标同为正数时对应类标为2，x坐标和y坐标同为负数时对应类标为1。通过高斯朴素贝叶斯分类分析的代码如下：
# -*- coding: utf-8 -*-
import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1, -1], [-2, -1], [-3, -2], [1, 1], [2, 1], [3, 2]])
Y = np.array([1, 1, 1, 2, 2, 2])
clf = GaussianNB()
clf.fit(X, Y)
pre = clf.predict(X)
print u"数据集预测结果:", pre
print clf.predict([[-0.8, -1]])
clf_pf = GaussianNB()
clf_pf.partial_fit(X, Y, np.unique(Y)) #增加一部分样本
print clf_pf.predict([[-0.8, -1]])
多项式朴素贝叶斯：sklearn.naive_bayes.MultinomialNB(alpha=1.0, fit_prior=True, class_prior=None)主要用于离散特征分类，例如文本分类单词统计，以出现的次数作为特征值。
参数说明：alpha为可选项，默认1.0，添加拉普拉修/Lidstone平滑参数；fit_prior默认True，表示是否学习先验概率，参数为False表示所有类标记具有相同的先验概率；class_prior类似数组，数组大小为(n_classes,)，默认None，类先验概率。
下面是朴素贝叶斯算法常见的属性和方法。
1) class_prior_属性
观察各类标记对应的先验概率，主要是class_prior_属性，返回数组。代码如下：
print clf.class_prior_
#[ 0.5 0.5]2) class_count_属性
获取各类标记对应的训练样本数，代码如下：
print clf.class_count_
#[ 3. 3.]3) theta_属性
获取各个类标记在各个特征上的均值，代码如下：
print clf.theta_
#[[-2. -1.33333333]
# [ 2. 1.33333333]]4) sigma_属性
获取各个类标记在各个特征上的方差，代码如下：
print clf.theta_
#[[-2. -1.33333333]
# [ 2. 1.33333333]]5) fit(X, y, sample_weight=None)
训练样本，X表示特征向量，y类标记，sample_weight表各样本权重数组。
#设置样本不同的权重
clf.fit(X,Y,np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))
print clf
print clf.theta_
print clf.sigma_ 输出结果如下所示：
GaussianNB()
[[-2.25 -1.5 ]
[ 2.25 1.5 ]]
[[ 0.6875 0.25 ]
[ 0.6875 0.25 ]]6) partial_fit(X, y, classes=None, sample_weight=None)
增量式训练，当训练数据集数据量非常大，不能一次性全部载入内存时，可以将数据集划分若干份，重复调用partial_fit在线学习模型参数，在第一次调用partial_fit函数时，必须制定classes参数，在随后的调用可以忽略。
import numpy as np
from sklearn.naive_bayes import GaussianNB
X = np.array([[-1,-1], [-2,-2], [-3,-3], [-4,-4], [-5,-5],
[1,1], [2,2], [3,3]])
y = np.array([1, 1, 1, 1, 1, 2, 2, 2])
clf = GaussianNB()
clf.partial_fit(X,y,classes=[1,2],
sample_weight=np.array([0.05,0.05,0.1,0.1,0.1,0.2,0.2,0.2]))
print clf.class_prior_
print clf.predict([[-6,-6],[4,5],[2,5]])
print clf.predict_proba([[-6,-6],[4,5],[2,5]])输出结果如下所示：
[ 0.4 0.6]
[1 2 2]
[[ 1.00000000e+00 4.21207358e-40]
[ 1.12585521e-12 1.00000000e+00]
[ 8.73474886e-11 1.00000000e+00]]可以看到点[-6,-6]预测结果为1，[4,5]预测结果为2，[2,5]预测结果为2。同时，predict_proba(X)输出测试样本在各个类标记预测概率值。
7) score(X, y, sample_weight=None)
返回测试样本映射到指定类标记上的得分或准确率。
pre = clf.predict([[-6,-6],[4,5],[2,5]])
print clf.score([[-6,-6],[4,5],[2,5]],pre)
#1.0最后给出一个高斯朴素贝叶斯算法分析小麦数据集案例，代码如下：
# -*- coding: utf-8 -*-
#第一部分 载入数据集
import pandas as pd
X = pd.read_csv("seed_x.csv")
Y = pd.read_csv("seed_y.csv")
print X
print Y
#第二部分 导入模型
from sklearn.naive_bayes import GaussianNB
clf = GaussianNB()
clf.fit(X, Y)
pre = clf.predict(X)
print u"数据集预测结果:", pre
#第三部分 降维处理
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(X)
print newData[:4]
#第四部分 绘制图形
import matplotlib.pyplot as plt
L1 = [n[0] for n in newData]
L2 = [n[1] for n in newData]
plt.scatter(L1,L2,c=pre,s=200)
plt.show()输出如下图所示：
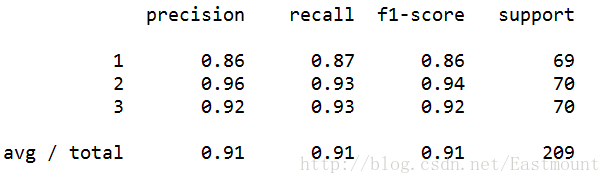
最后对数据集进行评估，主要调用sklearn.metrics类中classification_report函数实现的，代码如下：
from sklearn.metrics import classification_report
print(classification_report(Y, pre))运行结果如下所示，准确率、召回率和F特征为91%。
补充下Sklearn机器学习包常用的扩展类。
#监督学习
sklearn.neighbors #近邻算法
sklearn.svm #支持向量机
sklearn.kernel_ridge #核-岭回归
sklearn.discriminant_analysis #判别分析
sklearn.linear_model #广义线性模型
sklearn.ensemble #集成学习
sklearn.tree #决策树
sklearn.naive_bayes #朴素贝叶斯
sklearn.cross_decomposition #交叉分解
sklearn.gaussian_process #高斯过程
sklearn.neural_network #神经网络
sklearn.calibration #概率校准
sklearn.isotonic #保守回归
sklearn.feature_selection #特征选择
sklearn.multiclass #多类多标签算法
#无监督学习
sklearn.decomposition #矩阵因子分解sklearn.cluster # 聚类
sklearn.manifold # 流形学习
sklearn.mixture # 高斯混合模型
sklearn.neural_network # 无监督神经网络
sklearn.covariance # 协方差估计
#数据变换
sklearn.feature_extraction # 特征提取sklearn.feature_selection # 特征选择
sklearn.preprocessing # 预处理
sklearn.random_projection # 随机投影
sklearn.kernel_approximation # 核逼近三. 中文文本数据集预处理
假设现在需要判断一封邮件是不是垃圾邮件，其步骤如下：
- 数据集拆分成单词，中文分词技术
- 计算句子中总共多少单词，确定词向量大小
- 句子中的单词转换成向量，BagofWordsVec
- 计算P(Ci)，P(Ci|w)=P(w|Ci)P(Ci)/P(w)，表示w特征出现时，该样本被分为Ci类的条件概率
- 判断P(w[i]C[0])和P(w[i]C[1])概率大小，两个集合中概率高的为分类类标
1.数据集读取
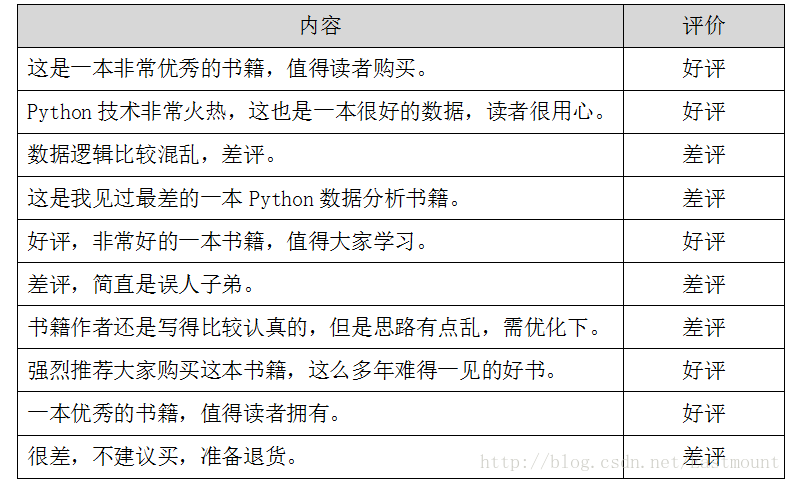
假设存在如下所示10条Python书籍订单评价信息，每条评价信息对应一个结果（好评和差评），如下图所示：
数据存储至CSV文件中，如下图所示。
下面采用pandas扩展包读取数据集。代码如下所示：
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"获取第一列内容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
for a in arrs:
print a输出结果如下图所示，同时可以通过data.iloc[:,0]获取第一列的内容。
2.中文分词及过滤停用词
接下来作者采用jieba工具进行分词，并定义了停用词表，即：
stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
完整代码如下所示：
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"获取第一列内容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用词
stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
print u"\n中文分词后结果:"
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精确模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用词的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output然后分词后的数据如下所示，可以看到标点符号及“这”、“我”等词已经过滤。
3.词频统计
接下来需要将分词后的语句转换为向量的形式，这里使用CountVectorizer实现转换为词频。如果需要转换为TF-IDF值可以使用TfidfTransformer类。词频统计完整代码如下所示：
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"获取第一列内容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用词
stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
print u"\n中文分词后结果:"
corpus = []
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精确模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用词的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output
corpus.append(output)
#计算词频
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer() #将文本中的词语转换为词频矩阵
X = vectorizer.fit_transform(corpus) #计算个词语出现的次数
word = vectorizer.get_feature_names() #获取词袋中所有文本关键词
for w in word: #查看词频结果
print w,
print ''
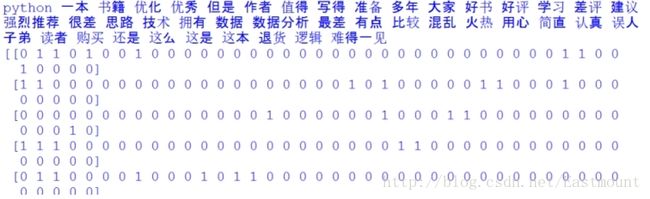
print X.toarray() 输出结果如下所示，包括特征词及对应的10行数据的向量，这就将中文文本数据集转换为了数学向量的形式，接下来就是对应的数据分析了。
如下所示得到一个词频矩阵，每行数据集对应一个分类类标，可以预测新的文档属于哪一类。
TF-IDF相关知识推荐我的文章： [python] 使用scikit-learn工具计算文本TF-IDF值
四. 朴素贝叶斯中文文本舆情分析
最后给出朴素贝叶斯分类算法分析中文文本数据集的完整代码。
# -*- coding: utf-8 -*-
import numpy as np
import pandas as pd
import jieba
#http://blog.csdn.net/eastmount/article/details/50323063
#http://blog.csdn.net/eastmount/article/details/50256163
#http://blog.csdn.net/lsldd/article/details/41542107
####################################
# 第一步 读取数据及分词
#
data = pd.read_csv("data.csv",encoding='gbk')
print data
#取表中的第1列的所有值
print u"获取第一列内容"
col = data.iloc[:,0]
#取表中所有值
arrs = col.values
#去除停用词
stopwords = {}.fromkeys(['，', '。', '！', '这', '我', '非常'])
print u"\n中文分词后结果:"
corpus = []
for a in arrs:
#print a
seglist = jieba.cut(a,cut_all=False) #精确模式
final = ''
for seg in seglist:
seg = seg.encode('utf-8')
if seg not in stopwords: #不是停用词的保留
final += seg
seg_list = jieba.cut(final, cut_all=False)
output = ' '.join(list(seg_list)) #空格拼接
print output
corpus.append(output)
####################################
# 第二步 计算词频
#
from sklearn.feature_extraction.text import CountVectorizer
from sklearn.feature_extraction.text import TfidfTransformer
vectorizer = CountVectorizer() #将文本中的词语转换为词频矩阵
X = vectorizer.fit_transform(corpus) #计算个词语出现的次数
word = vectorizer.get_feature_names() #获取词袋中所有文本关键词
for w in word: #查看词频结果
print w,
print ''
print X.toarray()
####################################
# 第三步 数据分析
#
from sklearn.naive_bayes import MultinomialNB
from sklearn.metrics import precision_recall_curve
from sklearn.metrics import classification_report
#使用前8行数据集进行训练，最后两行数据集用于预测
print u"\n\n数据分析:"
X = X.toarray()
x_train = X[:8]
x_test = X[8:]
#1表示好评 0表示差评
y_train = [1,1,0,0,1,0,0,1]
y_test = [1,0]
#调用MultinomialNB分类器
clf = MultinomialNB().fit(x_train, y_train)
pre = clf.predict(x_test)
print u"预测结果:",pre
print u"真实结果:",y_test
from sklearn.metrics import classification_report
print(classification_report(y_test, pre))输出结果如下所示，可以看到预测的两个值都是正确的。即“一本优秀的书籍，值得读者拥有。”预测结果为好评（类标1），“很差，不建议买，准备退货。”结果为差评（类标0）。
数据分析:
预测结果: [1 0]
真实结果: [1, 0]
precision recall f1-score support
0 1.00 1.00 1.00 1
1 1.00 1.00 1.00 1
avg / total 1.00 1.00 1.00 2但存在一个问题，由于数据量较小不具备代表性，而真实分析中会使用海量数据进行舆情分析，预测结果肯定页不是100%的正确，但是需要让实验结果尽可能的好。最后补充一段降维绘制图形的代码，如下：
#降维绘制图形
from sklearn.decomposition import PCA
pca = PCA(n_components=2)
newData = pca.fit_transform(X)
print newData
pre = clf.predict(X)
Y = [1,1,0,0,1,0,0,1,1,0]
import matplotlib.pyplot as plt
L1 = [n[0] for n in newData]
L2 = [n[1] for n in newData]
plt.scatter(L1,L2,c=pre,s=200)
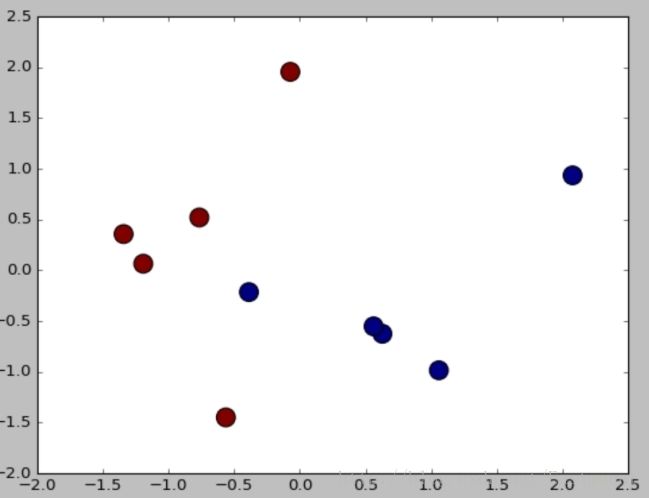
plt.show()输出结果如图所示，预测结果和真实结果都是一样的，即[1,1,0,0,1,0,0,1,1,0]。
(By:Eastmount 2018-01-24 中午1点 http://blog.csdn.net/eastmount/ )