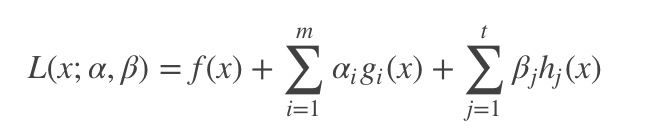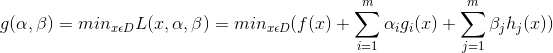机器学习知识点总结 - 拉格朗日乘子法（Lagrange Multiplier Method）详解

一直对拉格朗日乘子法不是理解的不是很透彻，今天决定要push一下自己，彻底的理解拉格朗日乘子法，希望对大家有所帮助。

接下来，我将从一下几个方面循序渐进的介绍拉格朗日乘子法：

目录

1 拉格朗日乘子法的基本定义和思想

1.2 拉格朗日乘子法的定义

1.3 KKT（Karush-Kuhn-Tucker）条件

1.3.1 为什么拉格朗日乘子法可以将带约束的优化问题转换成无约束的优化问题?

1.3.2 KKT条件的定义及作用？

2 对偶理论

2.1 原始问题、对偶问题的定义和它们之间的关系

2.2 拉格朗日乘子法中的对偶

2.2.1 对偶函数、原始问题、对偶问题以及一些基本结论

         2.2.2 对偶问题与原始问题的关系的推倒

---

1 拉格朗日乘子法的基本定义和思想

拉格朗日乘子法是一种优化算法，主要用于解决带约束条件下的优化问题。其基本思想就是通过引入拉格朗日乘子，将含有n个变量、k个约束条件的约束优化问题转化为含有（n+k）个变量的无约束优化问题。

1.1 原始问题描述

标准形式的带约束的优化问题可以用如下公式表示:

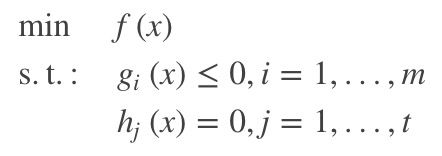公式（1.1）

在公式（1.1）中，是自变量，。该问题的定义域是非空集合为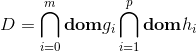, 其中 表示满足约束的自变量的集合。

 为满足约束条件的当前问题的最优解，为最优解对应的最优值。在当前问题中为最优极小值。

1.2 拉格朗日乘子法的定义

拉格朗日乘子法的基本思想就是将公式（1.1）中带有约束的最优化求解问题，转换为没有约束的优化问题。它的具体实现如公式（1.2）：

公式（1.2）

其中，是拉格朗日函数，就是拉格朗日乗子，且满足。成为primal变量，为dual变量（对偶变量）。

1.3 KKT（Karush-Kuhn-Tucker）条件

本节将详细介绍为什么拉格朗日乘子法可以将带约束的优化问题转换成无约束的优化问题，引出KKT条件的定义并介绍它的含义和作用。

1.3.1 为什么拉格朗日乘子法可以将带约束的优化问题转换成无约束的优化问题?

带约束的优化问题可以分为：等式约束的优化问题和不等式约束的优化问题。接下来，我们将从这两方面进行分析。

1.  等式约束的优化问题。

等式约束的优化问题定义为：假定为维向量，欲寻找的某个取值 ，使目标函数最小，且满足。

可用以下数学公式表示：

公式（1.3）

从几何角度来看，该问题的目标是在由方程确定的维度曲面上寻找能够使目标函数最小化的点。

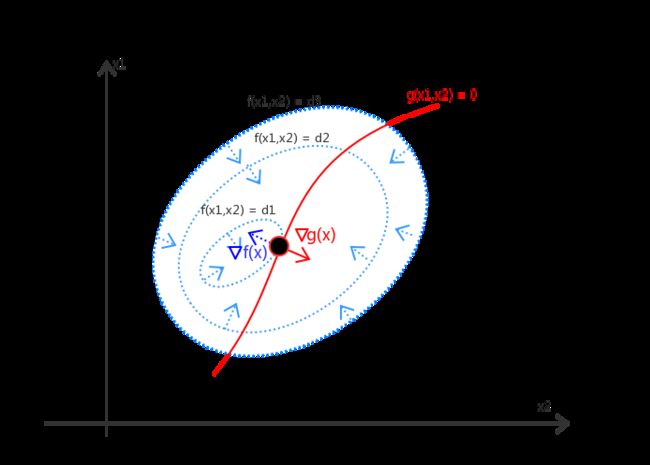
如图(a)所示，假设自变量包括两个维度。我们不难得出如下结论：

         1. 对于约束曲面上的任一点，该点的梯度正交于约束曲面

         2. 对于最优点，目标函数在最优点的梯度也正交于约束曲面

由此可知，在最优点，梯度和必然方向相同或者相反。即：存在，使得：

公式（1.4）

其中对应了拉格朗日函数中的拉格朗日乘子。

在该问题中，构造的对应的拉个朗日方程应为：。

不难发现，拉格朗日方程的对于的偏导数 设置为0则等价于公式（1.4）；同时，若将拉格朗日对求得的偏导设置为0，则得到对应的约束条件。

于是，可以证明：拉格朗日乘子法可以将原始的带等式约束的优化问题转化为对拉格朗日函数的无约束优化问题。

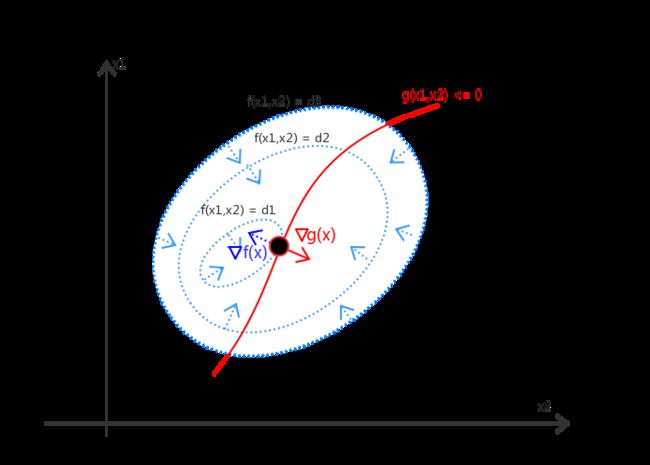
(a)  带等式约束的优化问题	(b) 带不等式约束的优化问题

 

2. 不等式约束的优化问题

现在我们考虑带不等式约束的优化问题。带不等式约束的优化问题可以写成：

公式（1.5）

在该种情况下，最优点的位置只有两种可能：要么存在于约束边界的区域内；要么存在于约束边界上。接下来我们分开分析一下这两种情况。

- 最优点在约束边界区域内

   在这种情况下，约束不起作用。我们可以直接通过条件求得最优点。

   等价于令后，再对拉格朗日函数求导

- 最优点在约束边界上

   这种情况类似于等式约束的优化问题。

   但需要注意的是，和必须反向，即存在，使得  。

在整合这两种可能，无论是还是，最优解都必须满足：。

综上可知，拉格朗日乘子法可以将 带不等式约束的优化问题 ，转化成在约束条件（公式（1.6））下对拉格朗日函数求最小化的优化问题。

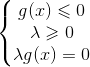公式（1.6）

其中公式(1.6)就是KKT条件。

同理，上述做法可以推广到多个约束的情况，即对于1.1节中描述的原始问题，首先我们可以利用拉格朗日乘子法构造拉格朗日方程及其对应的KKT条件：

对应KKT条件为：

公式（1.7）

求解1.1节介绍的原始问题等价于求解在满足KKT条件下的拉格朗日函数的最优化的问题。

至此，我们已经证明了拉格朗日乘子法的有效性，它确实可以将原始带约束的优化问题转化为求解满足KKT条件下的拉格朗日函数的最优化问题。

1.3.2 KKT条件的定义及作用？

从上一节的推倒过程我们可知，拉格朗日乘子法可以将带不等式约束的优化问题 ，转化成在KKT条件下对拉格朗日函数求最小化的优化问题。

这句话的含义是，当KKT条件被满足时，对拉格朗日函数的最优化问题才 等价于 原始问题。换句话说，KKT条件是拉格朗日取得可行解的必要条件。只有满足KKT条件，才能求出原始问题的最优解。

2 对偶理论

因为一个优化问题 可以从两个角度进行考察：即：主问题（primal问题）和对偶问题（dual问题）。本节中，我们将首先介绍原始问题、对偶问题及其定关系；然后介绍在带约束的优化问题中对偶函数的定义，以及在拉格朗日乘子法中原始问题的对偶问题是什么、以及对其对偶问题和原始问题的关系的推倒。

2.1 原始问题、对偶问题的定义和它们之间的关系

对偶问题：每一个线性规划问题都伴随有另一个线性规划问题，称为对偶问题。

原始问题（主问题）：原来的线性规划问题则称为原始线性规划问题，简称原始问题。

对偶问题与原始问题之间存在着下列关系：

       ① 目标函数对原始问题是极大化，对对偶问题则是极小化。

       ② 原始问题目标函数中的收益系数是对偶问题约束不等式中的右端常数，而原始问题约束不等式中的右端常数则是对偶问题中目标函数的收益系数。

       ③ 原始问题和对偶问题的约束不等式的符号方向相反。

       ④ 原始问题约束不等式系数矩阵转置后即为对偶问题的约束不等式的系数矩阵。

       ⑤ 原始问题的约束方程数对应于对偶问题的变量数，而原始问题的变量数对应于对偶问题的约束方程数。

       ⑥对偶问题的对偶问题是原始问题，这一性质被称为原始和对偶问题的对称性。

值得注意的是，如果我们能够获得原始问题或者对偶问题的中的任意一个问题的最优解，那么就相当于已经得到另外的问题的最优解。

2.2 拉格朗日乘子法中的对偶

2.2.1 对偶函数、原始问题、对偶问题以及一些基本结论

本节我们先给出对偶函数的定义；然后再介绍拉格朗日乘子法中的原始问题，对偶问题分别是什么。

• 对偶函数

拉格朗日函数的对偶函数的定义：拉格朗日函数关于取得的最小值。可表示为：

公式（2.1）

• 拉格朗日乘子法中的原始问题、对偶问题分别是什么

原始问题：1.1节给出的带约束的最优化问题

对偶问题：原始问题的对偶问题等于 拉格朗日函数的对偶函数的最优值，即：

公式（2.2）

• 一些基本结论

结论1：对偶函数 构成了原始问题（即公式（1.1））的最优值的下界，即: 

公式（2.3）

结论2：若对偶问题和原始问题均有最优解，设对偶问题的最优解对应的最优值为 ，即：

公式（2.4）

其中，的定义为公式（2.2）中给出，它是对偶函数的最优极大值。

2.2.2 对偶问题与原始问题的关系的推倒

接下来我们看一下为什么该结论成立：

结论1证明：

首先，在拉格朗日函数中，对于任意可行点，由于，并且 ，，因此有：

公式（2.5）

因而，根据上述不等式，我们可以推出：

公式（2.6）

因此，对任意可行点均有：

公式（2.7）

故而，可以推出公式（2.3）对于的不等式 成立，即：对偶函数是原始问题的最优值的下界。

结论2证明：

从结论1中可知，对偶函数构成了原始问题的最优值的下界，即: 。

故而，对偶函数的全部可能取解，都小于等于原始问题的最优解。

所以，对偶函数的最优值，也一定小于原始问题的最优解。

在目前研究的问题当中，对偶函数具有极大值，那么可以推出结论2：

公式（2.8）

至此，拉格朗日乘子法、对偶问题以及对偶问题和原始问题的关系介绍完毕。

3 拉格朗日乘子法实例

 

后记：

自参加完一个会议之后，自觉与大牛们差距甚远。往事不可追，后悔之前的荒废时间和不求甚解已经是徒劳。但求以后，以这篇文章为起点，要求自己不论工作亦或是求学都能踏踏实实，全力以赴。十年后再回首不会再有虚度光阴之感。