吴恩达机器学习系列理论加实践(二 、单变量线性回归及matlab实践)

二、单变量线性回归

2.1模型表示

同样以之前的房屋价格预测实例开始：


通过学习算法利用训练集训练模型h，对于新输入的数据size of house就可以输出其预测值price；
如何表达这个模型h：

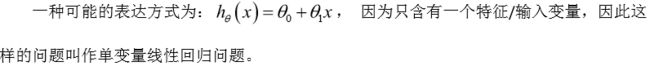
2.2 cost损失函数

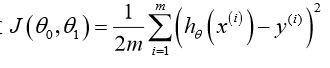
表示什么意思呢：首先2.1我们给出了模型预测函数h，其预测输出值即h(这里表示预测的房价)，而y表示真实的房价，他们之间差值的平方即表示此预测函数的代价函数，如上式子；
1/m是表示取所有预测差值平方的均值，1/2是为了后续便于计算并无特殊含义；示意图如下：


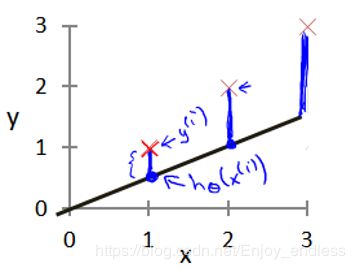
如上等高线表示了取不同的参数theta0/1对于最终代价函数J（）的影响值；
我们的目标就是是代价函数最小。

2.3代价函数的直观理解

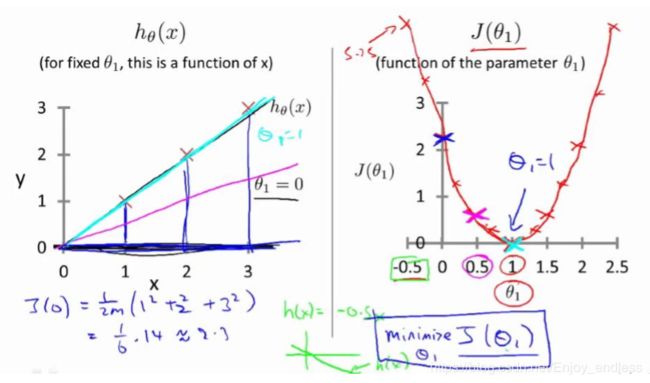
如上图所示学习到的模型h及真实的数据红叉之间的关系，当两者完全重合时，其代价函数(平方误差和)是为0的，而当其h的参数theta偏离1时其代价是逐步增加的(如右上图)

2.4梯度下降

以上有了代价损失函数h，而我们的目标是使其最小化，而如何使其最小化呢：
刚开始的时候我们随机初始化参数theta0/1得到代价函数值很大，此时我们的目标就是更新参数使其代价函数值下降最多，而下降最多的方向就是其点的负梯度方向：(对于不同的初始点，负梯度方向不同，最后得到的最优值可能不同，也就是局部最优点，如何寻找最优后续讨论)

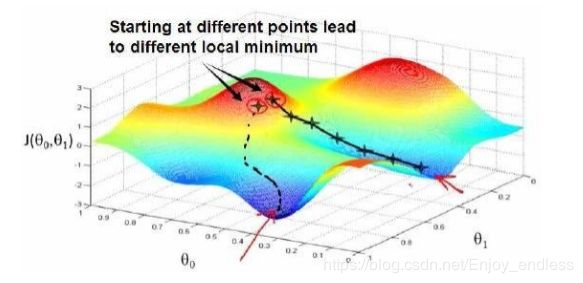
如上是一个迭代的过程，每更新一次找到最优的下降方向走一步，下一步同样基于当前的找负梯度方向进行进一步的更新；

如上求偏导再取负即是负梯度方向，乘子alpha表示我们每一步更新向前更新多少(具体取值后续讨论)，不断循环迭代直到收敛；

2.5梯度下降的直观理解

梯度下降即取负梯度方向，也即求导取负：

根据如上图分析：对于alpha(又叫学习率)的取值，如果太小则每次更新很小一步需要迭代很多次才能达到最低点，而如果alpha取太大则更新的时候可能会越过最低点而造成来回震荡，导致无法收敛；

再次分析如上梯度下降方法，当我们逐步逼近最低点的时候，其导数是越来越小的(平缓)，当步长不变时其实其更新同样是逐步减小的直到达到最低点即完成收敛；(这与上面的说alpha取值较大时函数不收敛是不冲突的，因为alpha取值过大的话其更新直接越过平滑处，其导数是不会减小的)

2.7梯度下降的线性回归

如上我们讲了线性回归模型及梯度下降法，那么我们将其二者结合：

其实也就是一个求导更新迭代的过程：

(在这里那个1/2与平方就直接约掉了)
则整体算法变成了：

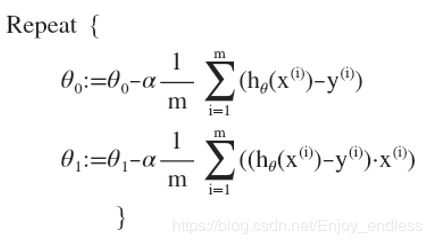
这一讲主要讲解了线性回归模型的整体训练过程，有了线性模型的定义，然后参数初始化、定义代价函数、利用梯度下降迭代、进行参数更新以至代价最小化达到收敛；

%matlab实践

A=eye(5);   %5*5对角矩阵

%加载数据并绘画
data=load('ex1data1.txt');
X=data(:,1);y=data(:,2);
plot(X,y,'gX','MarkerSize',5);  %g表示颜色，X表示显示形状，后面为形状大小
ylabel('Profit in $10000s');
xlabel('Population of City in 10000s');

%Cost and Gradient descent
m=length(y);
X=[ones(m,1),data(:,1)];   %增加一列代表偏置
theta=zeros(2,1);

iter=1500;
alpha=0.01;

J=sum(power(X*theta-y,2))/(2*m);  %损失函数
%梯度下降迭代更新参数
J_history=zeros(iter,1);
for iter2=1:iter
	t1=theta(1)-alpha*sum(X*theta-y)/m;  %偏置b求导结果
	t2=theta(2)-alpha*sum((X*theta-y).*X(:,2))/m;  % .*表示对应元素相乘
	theta(1)=t1;
	theta(2)=t2;
	J_history(iter2)=sum(power(X*theta-y,2))/(2*m);  %记录每一轮迭代的损失值

hold on; % keep previous plot visible
plot(X(:,2), X*theta, '-')
legend('Training data', 'Linear regression')
hold off % don't overlay any more plots on this figure

%根据训练得到的参数theta，可以进行相关预测
predict1=[1,3.5]*theta;
fprintf(predict1);

%三维绘画损失函数
theta0=linspace(-10,10,100); %-10到10等分100份
theta1=linspace(-1,4,100);

J_vals=zeros(length(theta0),length(teta1));
for i =1:length(theta0)
	for j=1:length(theta1)
		t=[theta(i);theta(j)];
		J_val(i,j)=sum(power(X*t-y,2))/(2*m);
	end
end

J_vals=J_vals';
surf(theta0,theta1,J_vals)
xlabel('theta0');ylabel('theta1');

%标准化
mu=zeros(1,size(X,2));   %初始化均值方差，其列数等于X列数(取列的均值方差)
sigma=zeros(1,size(X,2));

mu=mean(X);
sigma=std(X);
X_norm=(X-ones(size(X,1),1)*mu)./(ones(size(X,1),1)*sigma); %注意为点除

下一讲主要是讲解一些线性代数的基本知识，比较简单、有相关基础的可以直接略过。