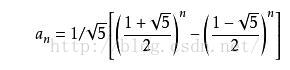斐波那契数列数组递推,普通递归,记忆化搜索,矩阵快速幂,和公式法
直接数列递推推的时候是O(n)的复杂度,查询的时候是O(1),但是当n很大的时候,数组空间可能有点力不从心
#include
#include
using namespace std;
int fb[45];
int main()
{
fb[0] = 0; fb[1] = 1;
for (int i = 2; i <= 45; i++) {
fb[i] = fb[i - 1] + fb[i - 2];
}
int n;
while (cin >> n) {
cout << fb[n] << endl;
}
return 0;
} 斐波那契数列递归定义 f(n) = f(n - 1) + f(n - 2) (n >= 2) f(1) = f(0) = 1
斐波那契解空间其实是一棵二叉树,斐波那契在若用普通递归算法,当n比较大的时候,直接递归在耗时比较长,原因是大量树节点重复计算,在n达到30,40左右就需要等待较长时间才能算出来一个结果
#include
#include
using namespace std;
int f(int n) {
if (n == 0) return 0;
if (n == 1) return 1;
return f(n - 1) + f(n - 2);
}
int main()
{
int n;
while (cin >> n) {
cout << f(n) << endl;
}
return 0;
} #include
#include
using namespace std;
int fb[1005], dp[1005];
int f(int n) {
if (n == 0) return fb[0] = 0;
if (n == 1) return fb[1] = 1;
if (fb[n] >= 0) { //不是-1说明之前计算过了,直接返回,相当于减掉一课子树,节省大量时间
return fb[n];
}
else {
return fb[n] = f(n - 1) + f(n - 2); //若没有是-1说明之前没有计算过,递归计算后更新fb[n]
}
}
int main()
{
memset(fb, -1, sizeof(fb)); //刚开始给fb打上标记
int n;
while (cin >> n) {
cout << f(n) << endl;
}
return 0;
} 但是当n特别大的时候记忆化就有些无能为力了,这时候可以通过采用矩阵快速幂来解决,顺便附加上poj3070一道题
| Time Limit: 1000MS | Memory Limit: 65536K | |
| Total Submissions: 11520 | Accepted: 8188 |
Description
In the Fibonacci integer sequence, F0 = 0, F1 = 1, and Fn = Fn − 1 + Fn − 2 for n ≥ 2. For example, the first ten terms of the Fibonacci sequence are:
0, 1, 1, 2, 3, 5, 8, 13, 21, 34, …
An alternative formula for the Fibonacci sequence is
Given an integer n, your goal is to compute the last 4 digits of Fn.
Input
The input test file will contain multiple test cases. Each test case consists of a single line containing n (where 0 ≤ n ≤ 1,000,000,000). The end-of-file is denoted by a single line containing the number −1.
Output
For each test case, print the last four digits of Fn. If the last four digits of Fn are all zeros, print ‘0’; otherwise, omit any leading zeros (i.e., print Fn mod 10000).
Sample Input
0 9 999999999 1000000000 -1
Sample Output
0 34 626 6875
Hint
As a reminder, matrix multiplication is associative, and the product of two 2 × 2 matrices is given by
Also, note that raising any 2 × 2 matrix to the 0th power gives the identity matrix:
#include
#include
using namespace std;
const int mod = 10000;
struct matrix { //用一个结构体来存矩阵
int node[2][2];
}ans, tem;
matrix muti(matrix a, matrix b) { //矩阵a乘b返回结果矩阵
matrix temp;
for (int i = 0; i < 2; i++) {
for (int j = 0; j < 2; j++) {
temp.node[i][j] = 0;
for (int k = 0; k < 2; k++) {
temp.node[i][j] = (temp.node[i][j] + (a.node[i][k] * b.node[k][j])) % mod;
}
}
}
return temp;
}
int quick_m(int b) {
ans.node[0][0] = ans.node[1][1] = 1; //ans初始化为单位矩阵
ans.node[0][1] = ans.node[1][0] = 0;
tem.node[0][0] = tem.node[0][1] = tem.node[1][0] = 1;
tem.node[1][1] = 0;
while (b) { //快速幂使用到矩阵乘法中
if (b & 1) {
ans = muti(ans, tem);
}
tem = muti(tem, tem);
b >>= 1;
}
return ans.node[0][1]; //注意返回的是F(n)
}
int main()
{
int n;
while (~scanf("%d", &n) && n != -1) {
printf("%d\n", quick_m(n));
}
return 0;
} 最后公式法,没什么好说的,关键是防误差,中间为了加速,用了对浮点型的快速幂,对于误差没有测试,仅供参考
#include
#include
#include
using namespace std;
double calc(double a, int b) {
double r = 1;
while (b) {
if (b & 1) {
r *= a;
}
a *= a;
b >>= 1;
}
return r;
}
int main()
{
int n, N;
int result;
cin >> N;
while (N--) {
cin >> n;
if (n == 1) result = 0;
else result = (int)((1 / sqrt(5)) * (calc((1 + sqrt(5)) / 2, n) + calc((1 - sqrt(5)) / 2, n)) + 0.5);
printf("%d\n", result);
}
return 0;
}