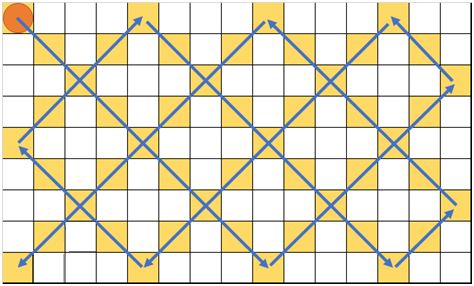
ACM-ICPC国际大学生程序设计竞赛北京赛区(2017)网络赛 G Bounce (规律)
Bounce
描述
For Argo, it is very interesting watching a circle bouncing in a rectangle.
As shown in the figure below, the rectangle is divided into N×M grids, and the circle fits exactly one grid.
The bouncing rule is simple:
1. The circle always starts from the left upper corner and moves towards lower right.
2. If the circle touches any edge of the rectangle, it will bounce.
3. If the circle reaches any corner of the rectangle after starting, it will stop there.
Argo wants to know how many grids the circle will go through only once until it first reaches another corner. Can you help him?
输入
The input consists of multiple test cases. (Up to 105)
For each test case:
One line contains two integers N and M, indicating the number of rows and columns of the rectangle. (2 ≤ N, M ≤ 109)
输出
For each test case, output one line containing one integer, the number of grids that the circle will go through exactly once until it stops (the starting grid and the ending grid also count).
2 2 2 3 3 4 3 5 4 5 4 6 4 7 5 6 5 7 9 15样例输出
2 3 5 5 7 8 7 9 11
39
比赛时一个小时没推出来的规律题 ,最后看到大佬给的代码以后发现我那样推根本不可能推出来,智商有限。话说这个规律也不是很了解,这种规律题都可以推出来,还是要膜一下。
代码实现:
#include
#include
#include
#include
#include
#include
#define ll long long
#define mset(a,x) memset(a,x,sizeof(a))
using namespace std;
const double PI=acos(-1);
const int inf=0x3f3f3f3f;
const double esp=1e-6;
const int maxn=1005;
const int mod=1e9+7;
int dir[4][2]={0,1,1,0,0,-1,-1,0};
ll gcd(ll a,ll b){return b?gcd(b,a%b):a;}
ll lcm(ll a,ll b){return a/gcd(a,b)*b;}
ll inv(ll b){if(b==1)return 1; return (mod-mod/b)*inv(mod%b)%mod;}
ll fpow(ll n,ll k){ll r=1;for(;k;k>>=1){if(k&1)r=r*n%mod;n=n*n%mod;}return r;}
int main()
{
ll n,m,a,b,temp,temp1,ans,c,d;
while(cin>>n>>m)
{
if(n>m)
swap(n,m);
temp=gcd(n-1,m-1);
temp1=(n-1)/temp+1;
a=(temp1-2)/2;
b=temp1-a-2;
c=(m-1)/temp/2;
d=(m-1-temp)/temp/2;
ans=b*c+a*d;
ans=(n-1)/temp*(m-1)+1-2*ans;
cout<