CUDA PTX ISA阅读笔记(二)
8. 第八章 指令集
这一章占了整个手册的一大半(百十来页吧),主要介绍各种指令,虽然页数很多,但是大多数指令都很简单。
8.1. 指令的形式和语义描述
这章就是主要描述每个PTX指令。除了指令的形式和语义之外还有一些例子来描述这些指令的使用场景。
8.2. PTX 指令
PTX指令一般有0-4个操作数,外加一个可选的判断标志,一般第一个都是目的地址,后面的是源地址,也可以有两个目的地址,比如:
setp.lt.s32 p|q, a, b; // p = (a < b); q = !(a < b);
8.3. 判断操作
就和C语言的判断是一样的,会返回一个true or false:
if (i < n)
j = j + 1;
setp.lt.s32 p, i, n; // p = (i < n)
@p add.s32 j, j, 1; // if i < n, add 1 to j还可以有分支:
setp.lt.s32 p, i, n; // compare i to n
@!p bra L1; // if False, branch over
add.s32 j, j, 1;
L1: ...8.3.1. 比较
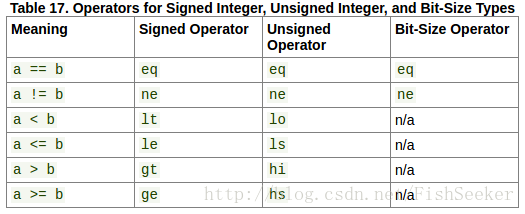
8.3.1.1. 整数比较
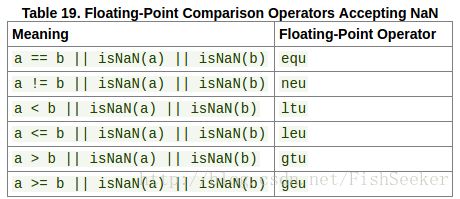
8.3.1.2. 浮点数比较
8.3.2. 对于判断值的操作
判断值(也就是true of false),可以使用or, xor, not, 和mov操作。并没有在整数和判断值的转换操作,但是setp可以从一个整数产生一个判断值:
selp.u32 %r1,1,0,%p; // convert predicate to 32-bit value
8.4. 指令操作数的类型
指令必须得带操作数的大小定义,而且一些操作需要多个类型定义:
.reg .u16 a;
.reg .f32 d;
cvt.f32.u16 d, a; // convert 16-bit unsigned to 32-bit floatFacebook8.4.1. 操作数超过指令要求的长度
就是当操作数的长度和操作指令长度要求不一致的时候的转换方法:
这是源操作数:
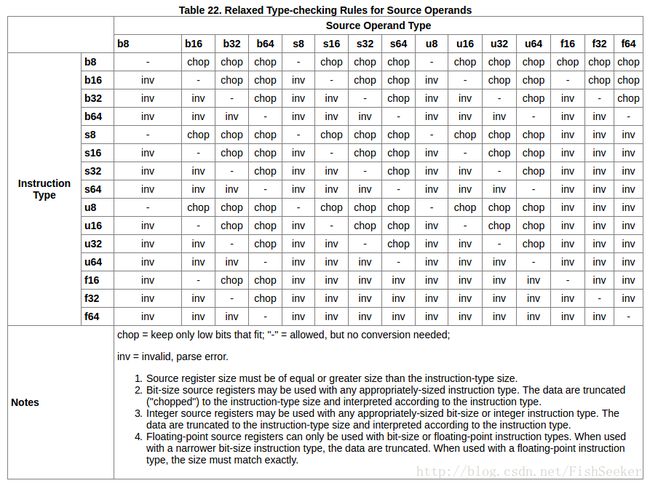
这是目的操作数:
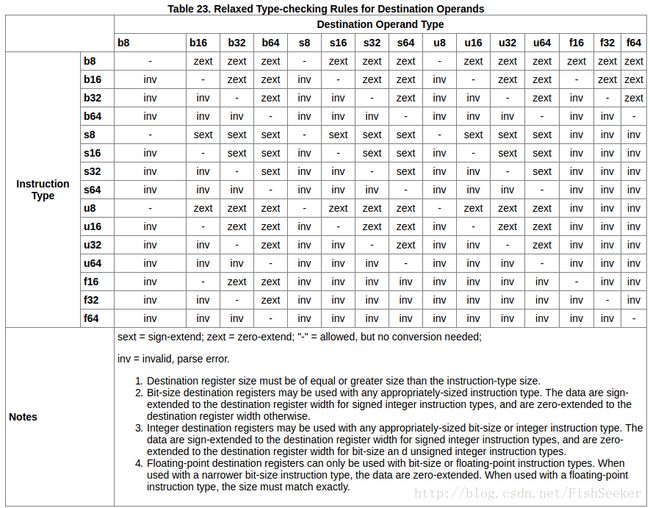
8.5. 在控制结构中线程的分支
一个CTA里的线程都是一起执行的,除非它们遇到了一些判断语句之类的,我们叫这种分开执行为分歧(divergent),称一块执行为统一(uniform),这两种情况都很常见。分支使得程序运行低效,应该尽可能快得使得线程统一。因此PTX提供了一个.uni语句用于在确定没有分支的时候,手动统一线程,以提高程序的运行效率。
8.6. 语义
就是使用C语言对PTX进行描述,除非C语言不能充分描述。
8.6.1. 十六位代码
GPU使用16位或者32位数据传输,如果在32位的情况下,16位的寄存器要被映射到32位的寄存器上,这会导致计算的不同(32位有高位和低位之分)。解决这个有两种办法,一个是转换到32位一种是机器无关的在哪都用16位。
8.7. 指令
8.7.1. 整数运算指令
8.7.1.1. 整数运算指令: add
加法:d = a + b;
//具体使用方法如下
add.type d, a, b;
add{.sat}.s32 d, a, b; // .sat applies only to .s32
//其中.type可以换成下面的这些
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };.sat的意思是限制结果的范围在MININT..MAXINT之间不要溢出,只适合于.s32类型
8.7.1.2. 整数运算指令: sub
减法:d = a - b;
sub.type d, a, b;
sub{.sat}.s32 d, a, b; // .sat applies only to
.s32 .type = { .u16, .u32, .u64,
.s16, .s32, .s64 };都和.add一样
8.7.1.3. 整数运算指令: mul
乘法:这里好像还区分高位低位
t = a * b;
n = bitwidth of type;
d = t; // for .wide
d = t<2n-1..n>; // for .hi variant
d = t1..0>; // for .lo variant 具体例子:
mul.wide.s16 fa,fxs,fys; // 16*16 bits yields 32 bits
mul.lo.s16 fa,fxs,fys; // 16*16 bits, save only the low 16 bits
mul.wide.s32 z,x,y; // 32*32 bits, creates 64 bit result8.7.1.4. 整数运算指令: mad
乘加:
t = a * b;
n = bitwidth of type;
d = t + c; // for .wide
d = t<2n-1..n> + c; // for .hi variant
d = t1..0> + c; // for .lo variant 这里也是有lo,hi之分。
//这里这个@p就是条件语句
@p mad.lo.s32 d,a,b,c;
mad.lo.s32 r,p,q,r;8.7.1.5. 整数运算指令: mul24
24位整数值的乘法:不太知道这有啥用
t = a * b;
d = t<47..16>; // for .hi variant
d = t<31..0>; // for .lo variant语法:
mul24{.hi,.lo}.type d, a, b;
.type = { .u32, .s32 };8.7.1.6. 整数运算指令: mad24
24位整数乘法:
t = a * b;
d = t<47..16> + c; // for .hi variant
d = t<31..0> + c; // for .lo vari基本和加法没啥区别:
mad24.lo.s32 d,a,b,c; // low 32-bits of 24x24-bit signed multiply.8.7.1.7. 整数运算指令: sad
最悲伤指令:d = c + ((a
sad.type d, a, b, c;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };8.7.1.8. 整数运算指令: div
除法:d = a/b。
div.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };8.7.1.9. 整数运算指令: rem
取余:d = a % b;
rem.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };8.7.1.10. 整数运算指令: abs
取绝对值:d = |a|;
abs.type d, a;
.type = { .s16, .s32, .s64 };8.7.1.11. 整数运算指令: neg
负数:d = -a;
neg.type d, a;
.type = { .s16, .s32, .s64 };8.7.1.12. 整数运算指令: min
最小值:d = (a < b) ? a : b; // Integer (signed and unsigned)
min.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };8.7.1.13. 整数运算指令: max
最大值:d = (a > b) ? a : b; // Integer (signed and unsigned)
max.type d, a, b;
.type = { .u16, .u32, .u64,
.s16, .s32, .s64 };8.7.1.14. 整数运算指令: popc
算一个数的二进制表示里有多少个1(这有啥用。。。)
.u32 d = 0;
while (a != 0) {
if (a & 0x1) d++;
a = a >> 1;
} 用起来倒是很简单:
popc.type d, a;
.type = { .b32, .b64 };8.7.1.15. 整数运算指令: clz
计算一个数的二进制开头有多少零(嗯。。。):
.u32 d = 0;
if (.type == .b32) {
max = 32; mask = 0x80000000;
}
else {
max = 64; mask = 0x8000000000000000;
}
while (d < max && (a&mask == 0) ) {
d++;
a = a << 1;
}语法:
clz.type d, a;
.type = { .b32, .b64 };8.7.1.16. 整数运算指令: bfind
这个是返回最高有效位的位置:
//讲真,每太看懂这解释
msb = (.type==.u32 || .type==.s32) ? 31:63;
// negate negative signed inputs
if ( (.type==.s32 || .type==.s64) && ( a & (1<u32 d = 0xffffffff;
for (.s32 i=msb; i>=0; i--) {
if (a & (1<break;}
}
if (.shiftamt && d != 0xffffffff) {d = msb - d; } 使用方法如下:
bfind.u32 d, a;
bfind.shiftamt.s64 cnt, X; // cnt is .u328.7.1.17. 整数运算指令: brev
这个比较好理解就是把每一位反转:
msb = (.type==.b32) ? 31 : 63;
for (i=0; i<=msb; i++) {
d[i] = a[msb-i];
}语法:
brev.type d, a;
.type = { .b32, .b64 };8.7.1.18. 整数运算指令: bfe
提取一个数的某一段二进制:
msb = (.type==.u32 || .type==.s32) ? 31 : 63;
pos = b & 0xff; // pos restricted to 0..255 range
len = c & 0xff; // len restricted to 0..255 range
if (.type==.u32 || .type==.u64 || len==0)
sbit = 0;
else
sbit = a[min(pos+len-1,msb)];
d = 0;
for (i=0; i<=msb; i++) {
d[i] = (i<len && pos+i<=msb) ? a[pos+i] : sbit;
}反正,参数的意思是这样的:
bfe.b32 d,a,start,len;从start开始取a的len位的数,赋值给d。
8.7.1.19. 整数运算指令: bfi
这个和上面那个异曲同工啊,是把某个数插入到另外一个数里:
msb = (.type==.b32) ? 31 : 63;
pos = c & 0xff; // pos restricted to 0..255 range
len = d & 0xff; // len restricted to 0..255 range
f = b;
for (i=0; i<len && pos+i<=msb; i++) {
f[pos+i] = a[i];
}语法:
bfi.b32 d,a,b,start,len;是把a插入到b的从start开始的len位,然后赋值给d。
8.7.1.20. 整数运算指令: dp4a
四路点积和:
d = c;
//Extract 4 bytes from a 32bit input and sign or zero extend based on input type.
Va = extractAndSignOrZeroExt_4(a, .atype);
Vb = extractAndSignOrZeroExt_4(b, .btype);
for (i = 0; i < 4; ++i) {
d += Va[i] * Vb[i];
}不太明白这和普通点积是啥子区别:
dp4a.u32.s32 d1, a1, b1, c1;另外主要这个只能在计算能力6.1或以上的机器上使用。
8.7.1.21. 整数运算指令: dp2a
和上面那个差不多,不过还是不太明白是搞啥的:
d = c;
// Extract two 16-bit values from a 32-bit input and sign or zero extend based on input type.
Va = extractAndSignOrZeroExt_2(a, .atype);
// Extract four 8-bit values from a 32-bit input and sign or zer extend
// based on input type.
Vb = extractAndSignOrZeroExt_4(b, .btype);
b_select = (.mode == .lo) ? 0 : 2;
for (i = 0; i < 2; ++i) {
d += Va[i] * Vb[b_select + i];
}举例:
dp2a.lo.u32.u32 d0, a0, b0, c0;
dp2a.hi.u32.s32 d1, a1, b1, c1;8.7.2. 长精度整数运算指令
8.7.2.1. 长精度运算指令: add.cc
这种是可以获得进位的加法,进位被写到CC.CF(这大概是个寄存器吧)。
语法:
add.cc.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };8.7.2.2. 长精度运算指令: addc
这个是将进位加上:d = a + b + CC.CF;
语法:
addc{.cc}.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };8.7.2.3. 长精度运算指令: sub.cc
这种是可以获得借位的减法,借位被写到CC.CF(这大概是个寄存器吧)。
语法:
sub.cc.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };8.7.2.4. 长精度运算指令: subc
这个是将进位加上:d = a - (b + CC.CF);
语法:
subc{.cc}.type d, a, b;
.type = { .u32, .s32, .u64, .s64 };8.7.2.5. 长精度运算指令: mad.cc
分高低位的乘加运算:
t = a * b;
d = t<63..32> + c; // for .hi variant
d = t<31..0> + c; // for .lo variant语法:
mad{.hi,.lo}.cc.type d, a, b, c;
.type = { .u32, .s32, .u64, .s64 };8.7.2.6. 长精度运算指令: madc
带精度的高地位运算:
t = a * b;
d = t<63..32> + c + CC.CF; // for .hi variant
d = t<31..0> + c + CC.CF; // for .lo variant语法:
madc{.hi,.lo}{.cc}.type d, a, b, c;
.type = { .u32, .s32, .u64, .s64 };8.7.3. 浮点数运算指令
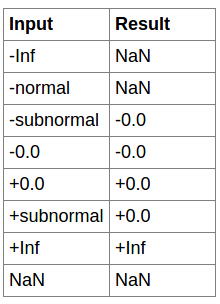
.ftz通过把非格式化浮点数的输入和结果冲洗成设备无关的保号零来保证后向兼容sm_1x设备。(所以到底是个蛇。。。)
8.7.3.1. 浮点数运算指令: testp
检测浮点数的性质:
testp.op.type p, a; // result is .pred
.op = { .finite, .infinite,
.number, .notanumber,
.normal, .subnormal };
.type = { .f32, .f64 };附上NaN的wiki解释
具体解释:
testp检测浮点数的设置,会返回true of false
- testp.finite
如果输入不是无穷大或者NaN返回true. - testp.infinite
如果是正负无穷返回true - testp.number
输入不是NaN返回true - testp.notanumber
输入是NaN返回true - testp.normal、
输入是个格式化浮点数(不是NaN,不是无限大) - testp.subnormal
输入是个非格式化浮点数(subnormal number)(不是NaN,不是无限大)
8.7.3.2. 浮点数运算指令: copysign
把一个输入数的符号拷贝给另一个:
//把a的符号拷贝给b然后用d返回
copysign.type d, a, b;
.type = { .f32, .f64 };8.7.3.3. 浮点数运算指令: add
加法:
add{.rnd}{.ftz}{.sat}.f32 d, a, b;
add{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };这其中,舍入规则为:
- .rn
mantissa LSB rounds to nearest even
- .rz
最低有效位变成0
- .rm
最低有效位变成负无穷
- .rp
最低有效位变成正无穷
8.7.3.4. 浮点数运算指令: sub
减法:
sub{.rnd}{.ftz}{.sat}.f32 d, a, b;
sub{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };8.7.3.5. 浮点数运算指令: mul
乘法:
mul{.rnd}{.ftz}{.sat}.f32 d, a, b;
mul{.rnd}.f64 d, a, b;
.rnd = { .rn, .rz, .rm, .rp };8.7.3.6. 浮点数运算指令: fma
乘加运算(人家有个很强的名字叫积和熔加运算):
fma.rnd{.ftz}{.sat}.f32 d, a, b, c;
fma.rnd.f64 d, a, b, c;
.rnd = { .rn, .rz, .rm, .rp };就是d = a*b + c;
8.7.3.7. 浮点数运算指令: mad
这个和上边那个是一样的,不知为啥搞出俩来:
mad{.ftz}{.sat}.f32 d, a, b, c; // .target sm_1x
mad.rnd{.ftz}{.sat}.f32 d, a, b, c; // .target sm_20
mad.rnd.f64 d, a, b, c; // .target sm_13 and higher
.rnd = { .rn, .rz, .rm, .rp };8.7.3.8. 浮点数运算指令: div
除法:
div.approx{.ftz}.f32 d, a, b; // fast, approximate divide
div.full{.ftz}.f32 d, a, b; // full-range approximate
divide div.rnd{.ftz}.f32 d, a, b; // IEEE 754 compliant
rounding div.rnd.f64 d, a, b; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };8.7.3.9. 浮点数运算指令: abs
绝对值:
abs{.ftz}.f32 d, a;
abs.f64 d, a;8.7.3.10. 浮点数运算指令: neg
相反数:
neg{.ftz}.f32 d, a;
neg.f64 d, a;语义:d = -a;
8.7.3.11. 浮点数运算指令: min
取两个数的最小值:
min{.ftz}.f32 d, a, b;
min.f64 d, a, b;语义:
if (isNaN(a) && isNaN(b)) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a < b) ? a : b;8.7.3.12. 浮点数运算指令: max
取最大:
max{.ftz}.f32 d, a, b;
max.f64 d, a, b;语义:
if (isNaN(a) && isNaN(b)) d = NaN;
else if (isNaN(a)) d = b;
else if (isNaN(b)) d = a;
else d = (a > b) ? a : b;8.7.3.13. 浮点数运算指令: rcp
取倒数:
rcp.approx{.ftz}.f32 d, a; // fast, approximate reciprocal
rcp.rnd{.ftz}.f32 d, a; // IEEE 754 compliant rounding
rcp.rnd.f64 d, a; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };8.7.3.14. 浮点数运算指令: rcp.approx.ftz.f6
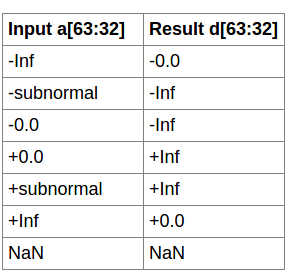
这个就是算倒数:rcp.approx.ftz.f64 d, a;
然后下面是倒数表:
8.7.3.15. 浮点数运算指令: sqrt
开平方:
sqrt.approx{.ftz}.f32 d, a; // fast, approximate square root
sqrt.rnd{.ftz}.f32 d, a; // IEEE 754 compliant rounding
sqrt.rnd.f64 d, a; // IEEE 754 compliant rounding
.rnd = { .rn, .rz, .rm, .rp };8.7.3.16. 浮点数运算指令: rsqrt
开平方的倒数:
rsqrt.approx{.ftz}.f32 d, a;
rsqrt.approx.f64 d, a;8.7.3.17. 浮点数运算指令: rsqrt.approx.ftz.f64
双精度开平方的倒数(真-精确):rsqrt.approx.ftz.f64 d, a;
8.7.3.18. 浮点数运算指令: sin
8.7.3.19. 浮点数运算指令: cos
8.7.3.20. 浮点数运算指令: lg2
8.7.3.21. 浮点数运算指令: ex2
上面四个就是数学函数:
sin.approx{.ftz}.f32 d, a;
cos.approx{.ftz}.f32 d, a;
lg2.approx{.ftz}.f32 d, a;
ex2.approx{.ftz}.f32 d, a;8.7.4. 半精度 浮点数运算指令
这种半精度的就是把一个数拆成hi和lo运算
8.7.4.1. 半精度 浮点数运算指令: add
加法:
add{.rnd}{.ftz}{.sat}.f16 d, a, b; // d, a, b are 16 bits in size
add{.rnd}{.ftz}{.sat}.f16x2 d, a, b; // d, a, b are 32 bits in size.
.rnd = { .rn };它的描述是这样的,和下面那些也差不多:
if (type == f16) {
d = a + b;
} else if (type == f16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
for (i = 0; i < 2; i++) {
d[i] = fA[i] + fB[i];
}
}8.7.4.2. 半精度 浮点数运算指令: sub
减法:
sub{.rnd}{.ftz}{.sat}.f16 d, a, b; // d, a, b are 16 bits in size
sub{.rnd}{.ftz}{.sat}.f16x2 d, a, b; // d, a, b are 32 bits in size.
.rnd = { .rn };8.7.4.3. 半精度 浮点数运算指令: mul
乘法:
mul{.rnd}{.ftz}{.sat}.f16 d, a, b; // d, a, b are 16 bits in size
mul{.rnd}{.ftz}{.sat}.f16x2 d, a, b; // d, a, b are 32 bits in size.
.rnd = { .rn };8.7.4.4. 半精度 浮点数运算指令: fma
熔石为甲命令。。。:
fma.rnd{.ftz}{.sat}.f16 d, a, b, c; // d, a, b, c are 16 bits in size
fma.rnd{.ftz}{.sat}.f16x2 d, a, b, c; // d, a, b, c are 32 bits in size.
.rnd = { .rn };8.7.5. 比较与选择指令
8.7.5.1. 比较与选择指令: set
就各种比较,然后返回一个bool值
//没c的时候就直接做运算
set.CmpOp{.ftz}.dtype.stype d, a, b;
//有c的时候要将结果和c比较之后返回
set.CmpOp.BoolOp{.ftz}.dtype.stype d, a, b, {!}c;
.CmpOp = { eq, ne, lt, gt, ge, lo, ls, hi, hs, equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.dtype = { .u32, .s32, .f32 };
.stype = { .b16, .b32, .b64, .u16, .u32, .u64, .s16, .s32, .s64, .f32, .f64 };这里的具体解释(代码比文字好看+1):
t = (a CmpOp b) ? 1 : 0;
if (isFloat(dtype))
d = BoolOp(t, c) ? 1.0f : 0x00000000;
else
d = BoolOp(t, c) ? 0xffffffff : 0x00000000;8.7.5.2. 比较与选择指令: setp
比较:
setp.CmpOp{.ftz}.type p[|q], a, b;
setp.CmpOp.BoolOp{.ftz}.type p[|q], a, b, {!}c;
.CmpOp = { eq, ne, lt, gt, ge, lo, ls, hi, hs, equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };
.type = { .b16, .b32, .b64, .u16, .u32, .u64, .s16, .s32, .s64, .f32, .f64 };主要的意思就是:
t = (a CmpOp b) ? 1 : 0;
p = BoolOp(t, c);
q = BoolOp(!t, c);
//examples
setp.lt.and.s32 p|q,a,b,r;
@q setp.eq.u32 p,i,n;8.7.5.3. 比较与选择指令: selp
语法:
selp.type d, a, b, c;
.type = { .b16, .b32, .b64, .u16, .u32, .u64, .s16, .s32, .s64, .f32, .f64 };语义:d = (c == 1) ? a : b;
8.7.5.4. 比较与选择指令: slct
和上边那个差不多:
slct.dtype.s32 d, a, b, c;
slct{.ftz}.dtype.f32 d, a, b, c;
.dtype = { .b16, .b32, .b64, .u16, .u32, .u64, .s16, .s32, .s64, .f32, .f64 };语义:d = (c >= 0) ? a : b;
8.7.6. 半精度比较指令
8.7.6.1 半精度比较指令: set
这个和全精度的区别就是,人家是按照一半一半比的:
set.CmpOp{.ftz}.f16.stype d, a, b;
set.CmpOp.BoolOp{.ftz}.f16.stype d, a, b, {!}c;
set.CmpOp{.ftz}.f16x2.f16x2 d, a, b;
set.CmpOp.BoolOp{.ftz}.f16x2.f16x2 d, a, b, {!}c;
//各种骚操作
.CmpOp = { eq, ne, lt, le, gt, ge, equ, neu, ltu, leu, gtu, geu, num, nan }; .BoolOp = { and, or, xor };
.stype = { .b16, .b32, .b64, .u16, .u32, .u64, .s16, .s32, .s64, .f32, .f64 };具体使用方法如下:
if (type == .f16) {
t = (a CmpOp b) ? 1 : 0;
d = BoolOp(t, c) ? 1.0 : 0.0;
} else if (type == .f16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
for (i = 0; i < 2; i++) {
d[i] = BoolOp(t[i], c) ? 1.0 : 0.0;
}
}8.7.6.2 半精度比较指令: setp
和上边那个差不多,就是这里的返回值是整数bool类型上面是浮点数。就是比较之后的返回值再和另外一个bool值(ptx这里叫predicate值)比较
setp.CmpOp{.ftz}.f16 p, a, b;
setp.CmpOp.BoolOp{.ftz}.f16 p, a, b, {!}c;
setp.CmpOp{.ftz}.f16x2 p|q, a, b;
setp.CmpOp.BoolOp{.ftz}.f16x2 p|q, a, b, {!}c;
.CmpOp = { eq, ne, lt, le, gt, ge, equ, neu, ltu, leu, gtu, geu, num, nan };
.BoolOp = { and, or, xor };语法:
if (type == .f16) {
t = (a CmpOp b) ? 1 : 0;
p = BoolOp(t, c);
} else if (type == .f16x2) {
fA[0] = a[0:15];
fA[1] = a[16:31];
fB[0] = b[0:15];
fB[1] = b[16:31];
t[0] = (fA[0] CmpOp fB[0]) ? 1 : 0;
t[1] = (fA[1] CmpOp fB[1]) ? 1 : 0;
p = BoolOp(t[0], c);
q = BoolOp(t[1], c);
}8.7.7. 逻辑与转化指令
8.7.7.1. 逻辑与转化指令: and
按位与:d = a & b;
语法:and.type d, a, b; .type = { .pred, .b16, .b32, .b64 };
8.7.7.2. 逻辑与转化指令: or
按位或:d = a | b;
语法:or.type d, a, b; .type = { .pred, .b16, .b32, .b64 };
8.7.7.3. 逻辑与转化指令: xor
按位异或:d = a ^ b;
语法:xor.type d, a, b; .type = { .pred, .b16, .b32, .b64 };
8.7.7.4. 逻辑与转化指令: not
非:d = ~a;
语法:not.type d, a, b; .type = { .pred, .b16, .b32, .b64 };
8.7.7.5. 逻辑与转化指令: cnot
那啥:d = (a==0) ? 1 : 0;
语法:cnot.type d, a, b; .type = { .b16, .b32, .b64 };
8.7.7.6. 逻辑与转化指令: lop3
这个稍微有点复杂,是对三个数进行逻辑操作,命令的格式是这样的:lop3.b32 d, a, b, c, immLut;使用这个要召唤一个函数,这个函数比如是这样的F(a & b & c),就会对a,b,c进行运算,然后得到的结果赋值给immLut,再返回给d就好了。
使用方法:
F = GetFunctionFromTable(immLut); // returns the function corresponding to immLut value
d = F(a, b, c);8.7.7.7. 逻辑与转化指令: shf
这个命令就是莫名其妙地移位,不知道实际有什么作用:
shf.l.mode.b32 d, a, b, c; // left shift
shf.r.mode.b32 d, a, b, c; // right shift
.mode = { .clamp, .wrap };具体的实现就是这样的,首先这个模式不知道是啥意思,然后就是取个移位的位数n,然后移位:
//根据模式和来确定要移动的位数
u32 n = (.mode == .clamp) ? min(c, 32) : c & 0x1f;
switch (shf.dir) { // shift concatenation of [b, a]
case shf.l: // extract 32 msbs
u32 d = (b << n) | (a >> (32-n));
case shf.r: // extract 32 lsbs
u32 d = (b << (32-n)) | (a >> n);
}
8.7.7.8. 逻辑与转化指令: shl
左移:d = a << b;
用法:shl.type d, a, b; .type = { .b16, .b32, .b64 };
8.7.7.9. 逻辑与转化指令: shr
右移:d = a >> b;
用法:shr.type d, a, b; .type = { .b16, .b32, .b64 };
8.7.8. 数据移动和转化指令
8.7.8.1. 缓存操作数
Load指令可以把内存中的一个单位的数据读取出来并装载到目标地址中
Store指令可以把一个目标地址中的数据读取出来并存储到内存中
1. load指令下的操作
- .ca 这个是把数据加载到所有的cache中,但是会造成coherent问题。要做的是将grid中的L1 cache设置为不可见
- .cg 只用L2 cache
- .cs cache stream中的操作
- .lu 最后一次使用
- .cv 不再cache
2. store指令下的操作
- .wb 回写模式。L1 L2都写。
- .cg cache到global
- .cs cache流
- .wt 直写模式。写回global和L2 cache。
Write-through(直写模式)在数据更新时,同时写入缓存Cache和后端存储。此模式的优点是操作简单;缺点是因为数据修改需要同时写入存储,数据写入速度较慢。
Write-back(回写模式)在数据更新时只写入缓存Cache。只在数据被替换出缓存时,被修改的缓存数据才会被写到后端存储。此模式的优点是数据写入速度快,因为不需要写存储;缺点是一旦更新后的数据未被写入存储时出现系统掉电的情况,数据将无法找回。