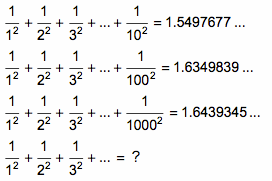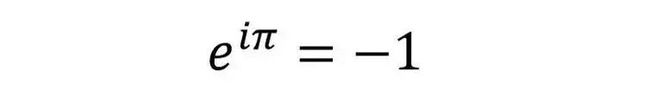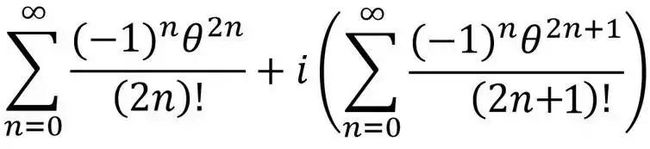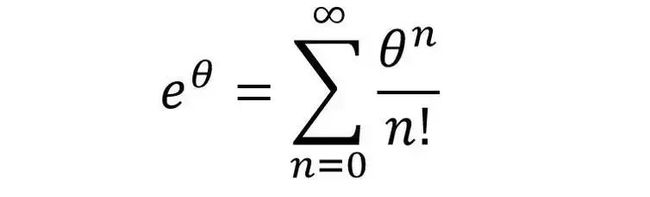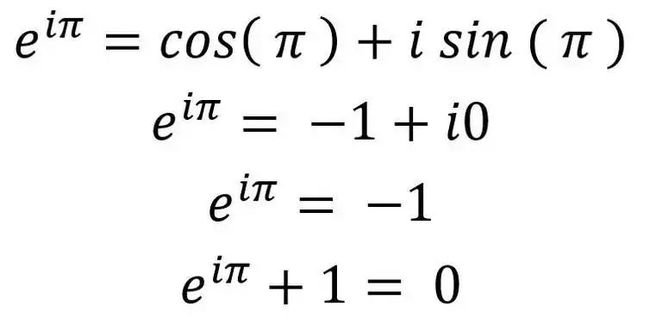数学里的π究竟牛在哪里
学过数学的同学想必都跟小编一样,都知道π ,不知道的不配做小编的盆友哒
,不知道的不配做小编的盆友哒 。
。
圆周率(Pi)是圆的周长与直径的比值,一般用希腊字母π表示,是一个在数学及物理学中普遍存在的数学常数。π也等于圆形之面积与半径平方之比。是精确计算圆周长、圆面积、球体积等几何形状的关键值。 在分析学里,π可以严格地定义为满足sin x = 0的最小正实数x。
由于圆周率π约等于3.14,因而人们将每年的3月14日设定为圆周率日。在这一天,世界各地的数学家和数学爱好者们欢聚一堂,歌颂赞美这个数学世界中的奇迹。
小编之前也搞不懂,圆周率 π 它究竟哪点吸引人了,能够让数学家们对它痴迷到如此地步?
其实,π 本身的存在就是一个奇迹:
不管一个圆有多大,它的周长和直径之比总是一个固定的数,它就是 3.141592653589793 … ,是一个无限不循环小数。我们把这个数就叫做圆周率,用希腊字母 π 来表示。
在几何问题中,圆周率扮演着非常重要的角色;然而更神奇的是,它也驰骋于几何以外的其它数学领域。
下面跟大家分享几个case:
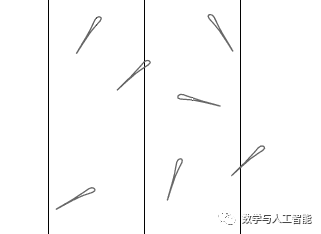
1、布丰投针实验
在地板上画一系列间距为 2 cm的平行线,然后把一根长度为 1 cm的针扔在地板上。那么,这根针与地板上的线条相交的概率是多少呢?
1733 年,法国博物学家布丰(Comte de Buffon)第一次提出了这个问题。1777 年,布丰自己解决了这个问题——这个概率值是 1/π。别的不说,就凭这自问自答地完成了超高级难度的数学问题的一件事,想必就让大家与小编一样,顶礼膜拜了吧 
另外,这个问题可以用微积分直接求解,也能利用期望值的性质得到一个异常精妙的解答。即使我们现在已经能轻易求出它的答案,结论依然相当令人吃惊——在这个概率问题上,竟然也有 π 的踪影。有人甚至利用投针法,求出过 π 的近似值来。
2、斯特林近似公式
我们把从 1 开始一直连乘到 n 的结果称作“n 的阶乘”,在数学中用 n! 来表示。也就是说:
![]()
1733 年,数学家亚伯拉罕·棣莫弗(Abraham de Moivre)发现,当 n 很大的时候,有:
其中 c 是某个固定常数。
不过棣莫弗本人并没有求出这个常数的准确值。几年后,数学家詹姆斯·斯特林(James Stirling)
指出,这个常数 c 等于 2π 的平方根。也就是说:
这个公式就被称作斯特林近似公式。
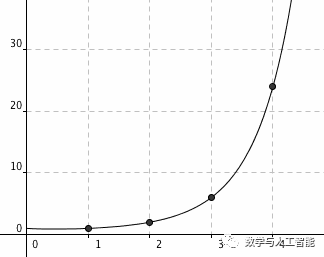
3、伽马函数
阶乘运算本来是定义在正整数上的,但我们可以很自然地把它扩展到所有的正数上——只需要寻找一条经过所有形如 (n, n!) 的整格点的曲线就可以了。由此定义出来的函数就叫做伽马函数,用希腊字母 Г 来表示。好了,神奇的事情出现了。我们有这样一个结论:
4、平方数的倒数和的极限
1 的平方分之一,加上 2 的平方分之一,加上 3 的平方分之一,这样一直加下去,结果会怎样呢?这是一个非常吸引人的问题。
从上表中可以看到,越往后加,得数变化幅度就越小。可以预料,如果无穷地加下去,得数将会无限接近于某一个固定的数。这个数是多少呢?
1735 年,大数学家欧拉(Euler)非常漂亮地解决了这一问题。神奇的是,这个问题的答案里竟然包含有 π:
5、两个整数互质的概率
如果两个整数的最大公约数为 1,我们就说这两个数是互质的。
例如,9 和 14 就是互质的,除了 1 以外它们没有其它的公共约数;9 和 15 就不互质,因为它们有公共的约数 3。可以证明这样一个令人吃惊的结论:任取两个整数,它们互质的概率是 6 / π 2 ,恰好是上面一个问题的答案的倒数。在一个纯数论领域的问题中出现了圆周率,无疑给小小的希腊字母 π 更添加了几分神秘。
6、欧拉恒等式
这是整个数学领域中最伟大,最神奇的公式:
![]()
这个公式用加法、乘法、乘方这三个最基础的运算,把数学中最神奇的三个常数(圆周率 π、自然底数 e、虚数单位 i)以及最根本的两个数(0 和 1)联系在了一起,没有任何杂质,没有任何冗余,漂亮到了令人敬畏的地步。
这个等式也是由大数学家欧拉发现的,它就是传说中的欧拉恒等式(Euler's identity)。《数学情报》杂志(The Mathematical Intelligencer)曾举办过一次读者投票活动,欧拉恒等式被评选为“史上最美的公式”。
然而,这些也都只是数学这个奇妙大世界的其中一角罢了。

Pi Day(3.14)刚刚过去,我们也奉上一篇和Pi有关的译作《π与最美的数学公式》,展示科学最单纯的美。据说文章每多一个方程,读者就会减少一半,不过小编很自信,因为下面列举的都是最美的。
--小编Z
今天我想谈谈π和数学意义上的的美。
要谈论这个,还有比十八世纪著名的欧拉公式更好的例子吗?
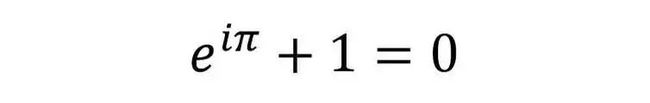
注意e指的是自然对数的底数。i是虚数单位,也就是-1的平方根。
这个公式经常被叫做“最美数学公式”,不过其实欧拉并没有真正的确切的把它写出来过。一个容易误解人的数学命名约定。相反,它是欧拉在证明指数增长和圆周运动的等价性时用到的公式的一种特殊情况。这个公式是这样的
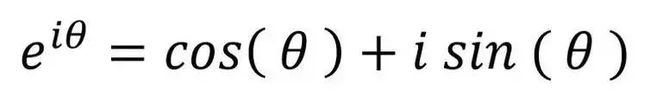
这个公式通常被称为cis函数,结合了余弦(cos)和正弦(sin)。theta是希腊字母。
美国理论物理学家理查德·费曼称其为“最引人注目的数学公式”。
欧拉社会的创始人——Ed Sandifer 曾在2007年的一篇好玩的文章中详细讨论了欧拉超过四十多年的方法,尝试去说明这个公式到底在干什么。在这里我将尽量用最少的公式来讲清楚这个故事。
这个公式干了什么?
欧拉公式包括了五个基本的数学常数0,1,i,e和π,以及它们之间的等号,加号和指数,以一种神秘而又有用的方式,组成了一个七字符的公式。它的等价形式也可以写成:
这个形式甚至更加简洁并且介绍了负数。
数学的一个共同特征是:发现总是首先被使用,然后才是被理解。18世纪法国数学家达朗贝尔写过代数是慷慨的,她经常给我们的答案超过了我们所问。
让我介绍一下构造欧拉公式的这些砖块的2000多年的历史。你不必去理解确切的数学,只要了解一下这些不同元素的不同起源,以及它们是怎么如此紧密地结合起来的。
等于 (=)
"="符号归因于1557年威尔士科学家罗伯特·雷科德。数学上关于相等的意思的讨论反映了同时又推动了哲学上关于确切描述的概念的讨论。
英国著名的逻辑学家伯特兰·罗素的例子是金星,称为晨星和昏星。一个反复提及的数学例子是0.99999999…和1是否相等。他们是,他们也不是。
零(0)
“0”的标记符号比 "= "更早。但是希腊人也好还是别的民族也好,都没有发现怎么去演算 0 的法则。一个数学上成熟的“0”的概念归功于大约公元650年的伟大的印度思想家Brahmagupta.
当“0”和另一个印度发明:进位计数法结合起来之后,计算数字便变得简单多了。这种能力直到15世纪或者更晚才传到欧洲。
1
没有“1”就没有先进的算法。“0”和“1”一起,我们有了二进制记数法和现代数字计算机。美国理论物理学家约翰·泰勒把这叫做“来自一点“(“来自比特“,英语双关,it from bit——译者)
这进一步导致了现代群论,代数,机密技术以及许多许多的其它知识。
i
虚数的使用大约开始于16到17世纪。法国哲学家和数学家笛卡尔就已经早早使用过它了,不过是以轻视的态度。
我们现在认为理所当然的数学概念有时候要花费几个世纪才能被接受和理解。难怪学生反抗虚数。这先是经过欧拉后来又经过德国数学家高斯的努力,虚数才真正的被开发起来了。“虚”这个词终于有了一个积极的数学内涵。
定义 i 作为-1 的平方根有一个非常美妙的结果。那就是一个n次多项式一定有n个(复)根了。比如说x^4=(x+1)(x-1)(x-i)(x+i), 它有四个根。这个导致了现在所谓复分析的发展。
如果没有复数,大多数现代数学和数学物理(比如量子力学)都不能工作了。
Pi(π)
π是半径为1的圆的面积和圆的周长。伟大的希腊数学家阿基米德(公元前287 - 前212)使用这个结论得到π近似值为22/7(3.141592…)。
欧拉提出了π的现代定义:即定义泰勒级数里面的余弦函数的最小的正系数为π/2.这有点复杂,但如果你只是想象这个级数是一个非常大的多项式,你会懂的。
这里 n!= 1 x 2 x···x n 叫做n的阶乘。这个十七世纪的另一个数学发现。
e
常数“e”起源于十七世纪,它被定义为自然对数的底数。到小数点后三位是2.718...,有点像π,这是一个无限不循环小数。
欧拉这位大师不光命名了“π”和“e”,他还意识到e^x也有一个花哨的泰勒级数。
然后令theta等于1,给出了一个关于e的有效公式。
现在我们知道了所有我们需要知道的砖块。我们需要对第二个公式做的是令theta等于π,利用简单的三角函数,我们知道sin(π)=0和cos(π)=-1,于是一步一步的约掉这个公式,我们便得到了美丽的第一个公式了。
什么是数学美?
正如你看到的,要看到这个公式的美我们必须理解这个公式的元素,至少是大概的理解。
罗素在他的《西方哲学史》上这样说:
“恰当的说,数学不仅涵括真理,亦表现最高等的美——这种美冷静而简朴,宛若雕塑,不诉诸我们任何柔弱的本性,没有绘画中亦或音乐中的华丽绚烂,但是纯粹得庄严,只有最伟大的艺术才能展示其严格的完美。”
大多数数学家都同意,一个美丽的公式一定是意料不到的,简洁的和有用的,有一种专业数学家能够感知到的高超的巧妙。
如果不得不列出来的话,大多数数学家会列出阿基米德,高斯,欧拉作为自古以来最杰出的五位数学思想家。另外两个是艾萨克·牛顿(微积分和力学)和波恩哈德·黎曼(黎曼几何和黎曼假设)。
同时拥有三位杰出的思想家和基本常数。难怪欧拉公式被人们崇拜地叫做最美丽的数学公式。
∑编辑 | 裴奕霖
来源 | 数学与人工智能
算法数学之美微信公众号欢迎赐稿
稿件涉及数学、物理、算法、计算机、编程等相关领域,经采用我们将奉上稿酬。
投稿邮箱:[email protected]