左偏树/斜堆——可并堆详解

所谓可并堆，顾名思义，就是可以合并的堆。
最常用的堆应该大家都知道，优先队列二叉堆，是吧
可是如果要求把两个堆合并，要怎么做？
一个个数pop提取出来然后再重新构造一个堆？
显然这种方法太暴力了..
有了可并堆，这个问题就可以被完美的解决了=V=
可并堆定义：

可并堆(Mergeable Heap)也是一种抽象数据类型，它除了支持优先队列的三个基本操作(Insert, Minimum, Delete-Min)，还支持一个额外的操作——合并操作：
H ← Merge(H1,H2)
Merge( ) 构造并返回一个包含H1和H2所有元素的新堆H。

以上抄摘自《算法合集之<左偏树的特点及其应用>》
那么问题来了 左偏树是什么？它拥有什么样的性质可以快速的合并呢？
好吧我先继续抄摘一段

左偏树(Leftist Tree)是一种可并堆的实现。左偏树是一棵二叉树，它的节点除了和二叉树的节点一样具有左右子树指针( left, right )外，还有两个属性：键值和距离(dist)。键值上面已经说过，是用于比较节点的大小。距离则是如下定义的：
节点i称为外节点(external node)，当且仅当节点i的左子树或右子树为空 ( left(i) = NULL或right(i) = NULL )；节点i的距离(dist(i))是节点i到它的后代中，最近的外节点所经过的边数。特别的，如果节点i本身是外节点，则它的距离为0；而空节点的距离规定为-1 (dist(NULL) = -1)。在本文中，有时也提到一棵左偏树的距离，这指的是该树根节点的距离。

首先我们来说一下左偏树的构造，他满足堆性质。简单来说，姜还是老的辣，权值还是老爹大。。
当然我们考虑小根堆的话权值是父节点较小，可以理解。
接下来有一个 普通堆没有的性质
左偏：左儿子的深度大于右儿子的深度
注意，这里的深度指的是他到他最下面一个小辈的距离，而不是到最上面的祖先。
。。原文里有一些没什么卵用的引理和性质我就不说了，显得冗余，看着都烦

接下来我们考虑两个堆的合并。
我们如果要合并 A和B两颗左偏树，我们只要把A的右子树去和B合并。然而我们必须要维护左偏树的性质，所以如果当合并后我们发现A的左儿子深度比右儿子小了，则交换左右儿子

if(dist[p[x].l]x].r])             swap(dist[p[x].l],dist[p[x].r]);

一直循环这个操作，直到。。。直到？
直到只有一颗子树啊！

if(!x)  return y;
if(!y)  return x;

x和y为当前要合并的两个子树

接下来一张图来解释这个合并过程
此图片转自原文

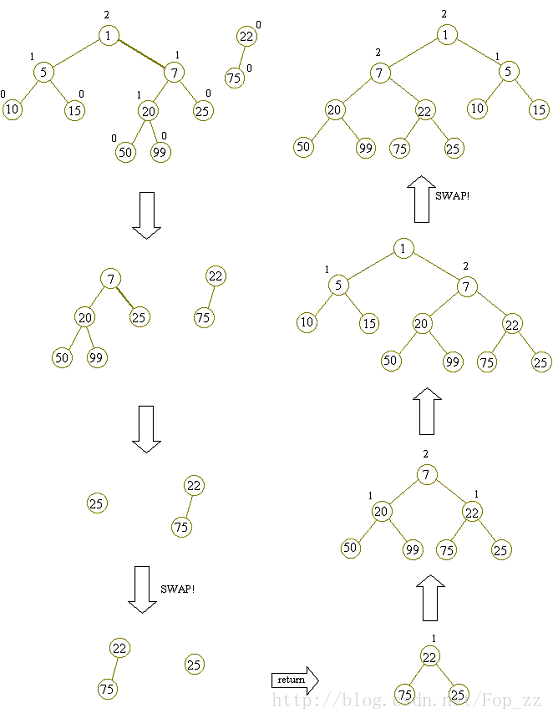
那么merge函数就成型了

inline int merge(int x,int y)
{
    if(!x)  return y;
    if(!y)  return x;
    if(p[x].val>p[y].val||(p[x].val==p[y].val&&x>y))    swap(x,y);
    int son=merge(p[x].r,y);
    p[x].r=son;
    if(dist[p[x].l]1;
    return x;
}

接下来是删除一个节点。
因为这个不是二叉堆。。所以并不是heap[1]就是堆顶
左偏树只有一条一条的边
所以我们如果想要知道堆顶，也就是最前面的祖先的话。。
并查集啊

inline int get(int x)
{
    return x==p[x].father?x:p[x].father=get(p[x].father);
}

这样就可以得到x所在的堆中的堆顶了
我们提取堆顶后，如何删除呢？
只要把左右子树合并就可以了啊
同时为了维护并查集的准确性，我们需要把堆顶的father记为新生成的堆的堆顶，这样在get的时候就可以get到新堆顶而不是那个被删除掉的点

    int tx=get(x);
                printf("%d\n",p[tx].val);
                alr[tx]=1;
                int the_aci=merge(p[tx].l,p[tx].r);
                p[tx].father=the_aci;//tx节点已经被删除，但是他的儿子们在get函数中需要通过tx来更新 
                p[the_aci].father=the_aci;

alr[tx]表示tx节点已经被删除

那么一个可并堆的基本操作就讲完了，还有一个就是要删除一个已知编号的节点。。
如果是堆顶，就很方便，如果不是，就需要删除后把子树不停的往堆顶上面merge，这份代码中我并没有用到这个操作。。
下面是bzoj1455 罗马游戏的代码
这个题可以说是比较好的可并堆模板题
CODE：

#include
#include
#include
#include
using namespace std;
struct point
{
    int l,r,father,val;
}p[1000001];
bool alr[1000001];//记录节点是否被删除 
int dist[1000001];
int n,m;
inline int get(int x)
{
    return x==p[x].father?x:p[x].father=get(p[x].father);
}
inline int merge(int x,int y)
{
    if(!x)  return y;
    if(!y)  return x;
    if(p[x].val>p[y].val||(p[x].val==p[y].val&&x>y))    swap(x,y);
    int son=merge(p[x].r,y);
    p[x].r=son;
    if(dist[p[x].l]1;
    return x;
}
int main()
{
    scanf("%d",&n);
    for(int i=1;i<=n;i++)
    {
        scanf("%d",&p[i].val),p[i].father=i;
    }
    scanf("%d",&m);
    for(int i=1;i<=m;i++)
    {
        char kind[5];
        scanf("%s",kind);
        if(kind[0]=='M')
        {
            int x,y;
            scanf("%d%d",&x,&y);
            if(alr[x]||alr[y])  continue;
            int tx=get(x),ty=get(y);
            if(tx==ty)  continue;
            else
            {
                int the_aci=merge(tx,ty);
                p[tx].father=p[ty].father=p[the_aci].father;
            }
        }
        else
        {
            int x;
            scanf("%d",&x);

            if(alr[x])
            {
                printf("0\n");
                continue;
            }else
            {
                int tx=get(x);
                printf("%d\n",p[tx].val);
                alr[tx]=1;
                int the_aci=merge(p[tx].l,p[tx].r);
                p[tx].father=the_aci;//tx节点已经被删除，但是他的儿子们在get函数中需要通过tx来更新 
                p[the_aci].father=the_aci;
            }
        }
    }
}

补：
刚才忘了讲斜堆了。。
其实所谓斜堆就是把dist去掉。。我手改一下上面的代码就成了斜堆了

if(dist[p[x].l]x].r])   swap(dist[p[x].l],dist[p[x].r]);
    dist[x]=dist[son]+1;

没错把这两句话删掉就成了斜堆
其实时间效率上差别并不大，一般斜堆都可以A掉左偏树的题目。
不过讲道理。。你斜堆都打出来了。。打个左偏树也不会累死你，而且可以毒瘤出题人会故意出题吧斜堆卡成RE。。因为不保证深度的情况下，递归层数很很多，系统栈可能会爆炸- -