一份非常详尽的FFT教学向博客

作为一个蒟蒻，在发现自己的FFT FFT 理解貌似有很多坑之后，我决定重写一篇 非常 非常 非常 详尽的FFT FFT 博客
这篇博客从0 0 喀什讲解，面向和我一样的ruo ruo ，所以，Dalao Dalao 退散
QwQ

在此特感谢function2 深入浅出的讲解，本文出自其讲义

多项式的数域

对于数域F F ,若a0,a1,a2,⋯,an∈F a0,a1,a2,⋯,an∈F

f(x)=n∑i=0aixi

为数域F上的一个多项式

其数域F上的所有多项式记作F[x]

同样的

Q[x]为有理数域的所有多项式

R[x]为实数域的所有多项式

C[x]为复数域的所有多项式

多项式的度数

多项式最高非零项的次数成为多项式的度数,用deg表示

f(x)=n∑i=0aixi

其中ai≠0

记作degf(x)=n

首一多项式(略)

加法与数乘运算(略)

多项式的线性空间

线性空间,即向量空间

满足线性性,封闭性

线性性: 量与量之间按比例呈线性的关系

封闭性: 其两个集合内元素进行二元运算结果必然在集合内

显然多项式加法,数乘运算满足线性性

记Fn[x]表示数域F上度数不超过n的全体多项式的集合,显然它们构成一个线性空间

多项式与向量满足一一对应的双射关系

f(x)=n∑i=0aixi⇔→a=(a0,a1,⋯,an)

多项式的系数表达

用一个n+1维的向量来表示Fn[x]中的全体多项式

多项式乘法

f(x)=n∑i=0aixi

g(x)=n∑i=0bixi

h(x)=f(x)∗g(x)=2∗n∑i=0i∑j=0ajbi−jxi

向量的卷积

多项式乘法中将多项式用向量表示其系数关系就是向量的卷积
f(x)=→a

g(x)=→b

h(x)=→c=→a⊗→b

ci=i∑j=0aj∗bi−j

多项式的幂

fk(x)=k∏i=1f(x)

多项式的复合

(f∘g)(x)=f(g(x))=n∑i=0aigi(x)

多项式的分治乘法

设n为2的自然数次幂,即∃k∈N,n=2k

设f,g∈F2n−1[x](一共有2n项)

将其分为两半

f(x)=f0(x)+xnf1(x)

g(x)=g0(x)+xng1(x)

显然的,f0,f1,g0,g1∈Fn−1[x]

(f×g)(x)=(f0×g0)(x)+xn(f0×g1+f1×g0)(x)+x2n(f1×g1)(x)

观察中间项,(f0×g1+f1×g0)(x)=((f0+f1)×(g0+g1)−f0∗g0−f1∗g1)(x)

那么我们就只需要处理(f0×g0)(x),(f1×g1)(x),((f0+f1)×(g0+g1))(x),规模均为原问题的一半

所以T(n)=3T(n2)+O(n)=O(nlog23)≈O(n1.585)

多项式的点值表达

degf(x)=n

x0,x1,x2,⋯,xn∈F

y0=f(x0),y1=f(x1),y2=f(x2),⋯,yn=f(xn)

则 (x0,y0),(x1,y1),(x2,y2),⋯,(xn,yn) 为多项式 f(x) 的点值表达

点值表达与系数表达满足双射关系

有范德蒙德矩阵V

(1x0x20⋯xn01x1x21⋯xn1⋮⋮⋮⋱⋮1xnx2n⋯xnn)(a0a1⋮an)=(y0y1⋮yn)

范德蒙德矩阵的行列式为∏j<i(xi−xj)

由于xi≠xj,所以行列式值非零,有唯一解

在x确定时,a,y有一一对应的双射关系

多项式的点值乘法(略)

多项式的插值

给出多项式的点值表达,求多项式的系数表达

1. 高斯消元O(n3)
2. 拉格朗日插值法O(n2)

高斯消元(略)

拉格朗日插值法

L(x)=n∑i=0∏j≠ix−xj∏j≠ixi−xjyi

不难发现 L(xi)=yi

所以L,f有相同的系数表达

自然数幂级数和

自然数幂级数和记作S
S(n,k)=n∑i=0ik

S(n,0)=n+1

//在这里我们将 00 看为 1
S(n,1)=n(n+1)2

S(n,2)=n(n+1)(2n+1)6

合理推测

S(n,k)为n的k+1次多项式

为了计算S(n,k)

选择xi=i(i=0,⋯,k),yi=S(xi,k)

插值求解即可

证明
(n+1)k+1−nk+1=k∑i=0(k+1i)ni

nk+1−(n−1)k+1=k∑i=0(k+1i)(n−1)i

⋮

1k+1−0k+1=k∑i=0(k+1i)0i

累加得
(n+1)k+1=k∑i=0(k+1i)S(n,i)

显然可得 S(n,k) 的度数

欧拉公式

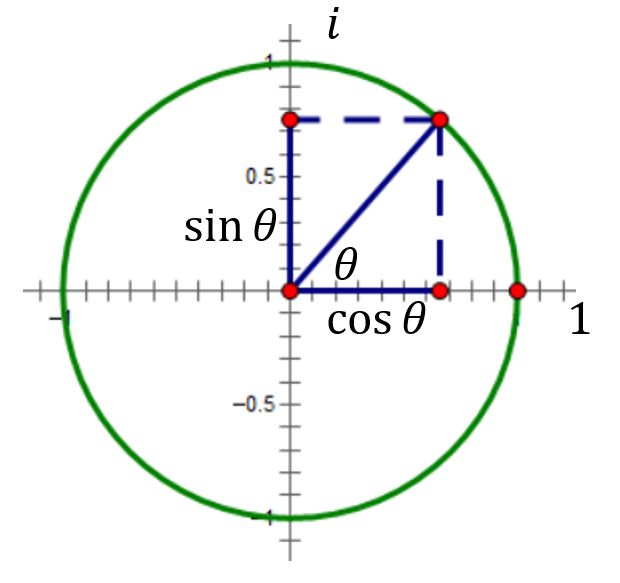
eiθ=cos(θ)+isin(θ)

几何意义上是单位圆上角度为 θ 的点

单位复数根

考虑构造一个x，使得xn=1

由欧拉公式可得e2kπi=1

则xn=e2kπi,x=e2kπin

当k=1 时，令ωn=e2πin，称为主n次单位根

wkn=e2kπin=cos(2kπn)+isin(2kπn)

由三角函数的周期性T=2π，不难得到wkn的周期性

wkn=wkmodnn

wnn=w0n=1

当k=0,1,2,⋯,n−1时，得到w0n,w1n,w2n,⋯,wn−1n，称为n次单位复数根

单位复数根的性质

消去引理：对于常数d>0，有wdkdn=wkn
折半引理：若n为偶数，则n次单位复数根的平方的集合就是n2次单位复数根的集合。特别的，每个n2次单位复数根出现两次
求和引理：
n−1∑i=0(wkn)i={nn∣k0n∤k

离散傅里叶变换(DFT)

多项式的系数表达式f=(a0,a1,a2,⋯,an−1)，求出在x0=w0n,x1=w1n,x2=w2n,⋯,xn−1=wn−1n初的点值

yk=f(xk)=f(wkn)

输出向量y=(y0,y1,y2,⋯,yn−1)

代入范德蒙德矩阵得：

(1w0nw0n2⋯w0nn−11w1nw1n2⋯w1nn−1⋮⋮⋮⋱⋮1w(n−1)nw(n−1)n2⋯w(n−1)nn−1)(a0a1⋮an−1)=(y0y1⋮yn−1)

此过程称为长度为 n 的离散傅里叶变换，记作 y=DFTn(f)

注意： 多项式的系数表达式的度数为n−1，而单位根为n次单位复数根

快速傅里叶变换(FFT)

f=(a0,a1,a2,⋯,an−1)

将奇数项，偶数项分别提出，得到构造出两个度为n2的系数表示（假设n为偶数）

f0=(a0,a2,a4,⋯,an−2)

f1=(a1,a3,a5,⋯,an−1)

那么f(x)=f0(x2)+x∗f(1)(x2)

设k<n2

f(wkn)=f0(w2k2)+wknf1(w2kn)=f0(wkn2)+wknf1(wkn2)

f(wk+n2n)=f0(w2k+nn)+wk+n2nf1(w2k+nn)=f0(wkn2)−wknf1(wkn2

令yk=f(wkn),y[0]k=f0(wkn2),y[1]k=f1(wkn2)

那么

yk=y[0]k+wkny[1]k

yk+n2=y[0]k−wkny[1]k

这一系列操作称为蝴蝶操作，wkn称为旋转因子

每次递归求得y[0]k,y[1]k，问题规模变为n2)，合并得到yk

T(n)=2T(n2)+O(n)=O(nlogn)

逆离散傅里叶变换(IDFT)

多项式的点值表达式(w0n,y0),(w1n,y1),(w2n,y2),⋯,(wn−1n,yn−1)，转化为系数表达式

尝试求得范德蒙德矩阵的逆矩阵V−1

即求VnV−1n=In

即vTiv−1j={1i=j0i≠j，其中vTi为V的行向量，T为转置，v−1j为V−1的列向量

vTi=(w0in,w1in,w2in,⋯,w(n−1)in)

联系求和定理

n−1∑i=0(wkn)i={nk=00k≠0

那么构造v−1j=1n(w−0jn,w−1jn,w−2jn,⋯,w−(n−1)jn)T

验证：

vTiv−1j=1nn−1∑k=0(wi−jn)k={ni=j0i≠j

将Va=y同乘V−1得a=yV−1，即：

1n(1w−0nw−0n2⋯w−0nn−11w−1nw−1n2⋯w−1nn−1⋮⋮⋮⋱⋮1w−(n−1)nw−(n−1)n2⋯w−(n−1)nn−1)(y0y1⋮yn−1)=(a0a1⋮an−1)

可见，a是系数表达y=(y0,y1,y2,⋯,yn−1)的多项式在w0n,w1nm,w2n,⋯,wn−1n处取的的点值除以n

在这些位置求出点值的过程被称为逆离散傅里叶变换，记作DFT−1n(y)，只需要对前面的DFT稍加修改即可实现

卷积定理

设a,b为n维向量，a,b的卷积c=a⊗b满足：

ci=i∑j=0aj∗bi−j

通过多项式乘法与其系数表达卷积的关系可以得到:

c=DFT−12n(DFT2n(a)∗DFT2n(b))

FFT的迭代实现

对于n=2k,考虑第i次分治（第i层）

二进制第i位为0，放入左侧，最终位置的第k−i位为0

二进制第i位为1，放入右侧，最终位置的第k−i位为1

不难发现，最终位置的二进制为原来位置的逆序

FFT题目：

BZOJ 3160 万径人踪灭

BZOJ 3527 力

BZOJ 4259 残缺的字符串

HDU 4609 3-idiots

codechef Prime Distance On Tree

看完记得点个赞哦