奇异值分解（SVD）

在线性代数中我们都学习过，对于满秩的方阵，有$Ax=\lambda x$成立，其中A是$n\ast n$的矩阵，λ是A的一个特征值，x为A对应λ的特征向量。

根据求出的特征值和特征向量，我们就可以将矩阵A分解，将其表达为另一种形式。假设A求出的特征值为$\lambda 1\le \lambda 2\le \lambda 3\le \dots \dots \le \lambda n$，而对应的特征向量为$w1,w2,\dots \dots ,wn$。如果特征向量间是线性无关的，则A可以表示为如下的形式$$A=W\Sigma W^{-1}$$

其中W是n个特征向量所组成的$n\ast n$的矩阵，∑是对角线元素为特征值的$n\ast n$的矩阵。将n个特征向量标准化满足$$||w_i|{|}_2=1$$或 $$w_i^T{w}_i=1$$则这n个向量为标准正交基，满足$$W^{T}W=I$$即$$W^T=W^{-1}$$将其称为酉矩阵。根据$$W^T=W^{-1}$$我们将A可以表达为$$A=W\Sigma W^T$$

比如在之前的线性回归算法中，如果X是这样的方阵，我们就可以求出它的闭式解。但是如果不是这样的方阵，该怎么解决呢？那就该奇异值分解SVD出场了。

首先给出使用SVD后A的表达式：$$A=U\Sigma V^T$$其中U是$m\ast m$的矩阵，$\Sigma$是$m\ast n$的矩阵，只有对角线元素不为零，将其中的元素称之为奇异值，V是$n\ast n$的矩阵。

那么我们如何求出这三个矩阵呢？

• V的计算
  将A的转置和A相乘，得到$n\ast n$的方阵$$A{A}^T$$这样就可以使用方阵的分解方式，得到$$(A^{T}A)v_i={\lambda }_i{v}_i$$
  将n个特征值所对应的特征向量，将其同样组成$n\ast n$的方阵，即$V$。

• U的计算
  将A和A的转置相乘，得到$m\ast m$的方阵$$A^{T}A$$这样就可以使用方阵的分解方式，得到$$(A{A}^T)u_i={\lambda }_i{u}_i$$
  同样将m个特征值所对应的特征向量，将其同样组成$m\ast m$的方阵，即$U$ 。

• Σ的计算
  因为有$V^T=V^{-1}$所以在SVD的表达式两边同乘以V，有如下的推导
  $$A=U\Sigma V^T\Rightarrow AV=U\Sigma V^{T}V\Rightarrow AV=U\Sigma \Rightarrow A{v}_i={\sigma }_i{u}_i\Rightarrow {\sigma }_i=A{v}_i/u_i$$

其中${\sigma }_i$就是我们要求的奇异值，将其组合得到$\Sigma$。

从中我们可以看到特征值矩阵等于奇异值矩阵的平方，即特征值和奇异值满足如下的关系：${\sigma }_i=\sqrt{{\lambda }_i}$，这样我们通过λi就可以求出奇异值。

因此有了SVD后我们就可以分解任意形式的矩阵，可以这样说：任意的矩阵X都可以转换为正交矩阵、对角阵和另外一个正交矩阵的乘积。

下面这个图很形象的表示了SVD中各矩阵之间的关系

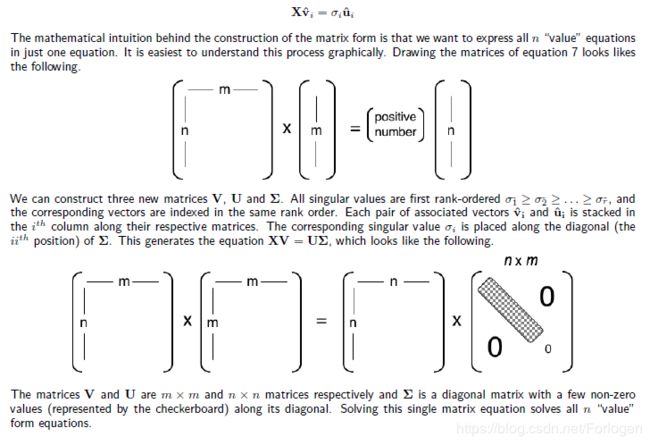
下面通过一个例子来看一下SVD是如何操作。假设$A$是$$\mathbf{A}=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)$$则根据上面所讲的原理求出相应的矩阵：
$$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)=\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$$ $$\mathbf{A}{\mathbf{A}}^{\mathbf{T}}=\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{ccc}0& 1& 1\\ 1& 1& 0\end{array}\right)=\left(\begin{array}{ccc}1& 1& 0\\ 1& 2& 1\\ 0& 1& 1\end{array}\right)$$

它们所对应的特征值和特征向量为
$${\lambda }_1=3;v_1=\left(\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right);{\lambda }_2=1;v_2=\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)$$

$${\lambda }_1=3;u_1=\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right);{\lambda }_2=1;u_2=\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right);{\lambda }_3=0;u_3=\left(\begin{array}{c}1/\sqrt{3}\\ -1/\sqrt{3}\\ 1/\sqrt{3}\end{array}\right)$$

利用${\lambda }_i$求出奇异值：$$\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_1\left(\begin{array}{c}1/\sqrt{6}\\ 2/\sqrt{6}\\ 1/\sqrt{6}\end{array}\right)\Rightarrow {\sigma }_1=\sqrt{3}$$

$$\left(\begin{array}{cc}0& 1\\ 1& 1\\ 1& 0\end{array}\right)\left(\begin{array}{c}-1/\sqrt{2}\\ 1/\sqrt{2}\end{array}\right)={\sigma }_2\left(\begin{array}{c}1/\sqrt{2}\\ 0\\ -1/\sqrt{2}\end{array}\right)\Rightarrow {\sigma }_2=1$$

则A使用SVD可表示为
$$A=U\Sigma V^T=\left(\begin{array}{ccc}1/\sqrt{6}& 1/\sqrt{2}& 1/\sqrt{3}\\ 2/\sqrt{6}& 0& -1/\sqrt{3}\\ 1/\sqrt{6}& -1/\sqrt{2}& 1/\sqrt{3}\end{array}\right)\left(\begin{array}{cc}\sqrt{3}& 0\\ 0& 1\\ 0& 0\end{array}\right)\left(\begin{array}{cc}1/\sqrt{2}& 1/\sqrt{2}\\ -1/\sqrt{2}& 1/\sqrt{2}\end{array}\right)$$

参考：

奇异值分解(SVD)原理与在降维中的应用

机器学习中SVD总结