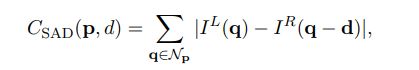《Stereo Matching by Training a Convolutional Neural Network to Compare Image Patches》论文阅读之MC-CNN
通过训练卷积神经网络比较图像块的立体匹配
project主页:https://github.com/jzbontar/mc-cnn
基于patch的提取与比较,学习其相似性得到一个matching cost,并将正确匹配的patch定义为正样本,其他为负样本。
后处理包括:cross-based cost aggregation, semiglobal matching, a left-right consistency check, subpixel enhancement, a median filter, and a bilateral lter.
fast 和accurate两个版本
LeCun经典论文
摘要
我们提出了一种从经过矫正的图像对中提取深度信息的方法。我们的方法集中在许多立体视觉算法的第一阶段:匹配代价计算。我们通过使用卷积神经网络进行小图像块的相似性度量来解决这个问题。我们使用相似和不相似的图像对构建二元分类数据集来进行有监督的训练。针对这个任务,我们检测了两个网络架构:一个是速度导向的, 另一个是准确性导向的。卷积神经网络的输出用于初始化立体匹配代价。一系列后处理步骤如下:基于交叉的代价聚合,半全局匹配,左右一致性检查,亚像素增强,一个中值滤波器和一个双边滤波器。我们用KITTI 2012,KITTI 2015和 Middlebury的立体视觉数据集来评估我们的方法,并发现它在所有的三大数据集中的表现均优于其他方法。
1.介绍
考虑以下问题:给定由不同水平位置的相机拍摄的两个图像,我们希望计算左图像中每个像素的视差d。 视差指的是同一对象在左图像和右图像中的水平位置的差异——同一对象在左图像中的位置为(x,y),在右图像中的位置为(x-d,y)。 如果我们知道一个对象的视差,我们可以使用以下关系计算它的深度z:
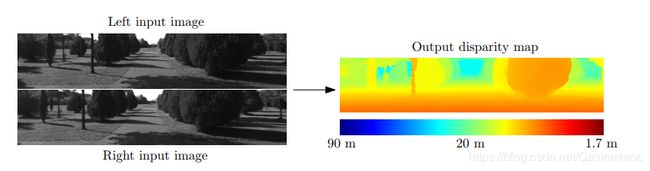
图1: 输入是来自左侧和右侧相机的一对图像。 两个输入图像的差异主要在对象的水平位置上(其他的差异是由反射,遮挡和透视失真引起的)。注意靠近相机的对象比远离相机的对象有更大的视差。右图的输出是一个密集的视差图,暖色表示更大的视差值(和较小的深度值)
其中f是相机的焦距,B是相机中心之间的距离。图 1描述了输入和通过我们的方法处理的输出。
上述的立体匹配问题在许多领域中都是非常重要的,例如自动驾驶,机器人技术,中间视图生成和3D场景重建。 根据Scharstein和Szeliski (2002)的分类,一个典型的视觉算法包括四个步骤:匹配代价计算,代价聚合,优化,视差精化。 根据 Hirschmüller和Scharstein (2009)的分类,我们认为前两个步骤是计算匹配代价和后两个步骤为立体视觉法。我们工作的重点是计算好匹配代价。
我们建议对图像块对训练卷积神经网络( LeCun等人,1998年),其中真实的视差是已知的(例如,由激光雷达或结构光获得)。网络的输出用于初始化匹配代价。我们还需进行许多不是新颖的但是必要的后处理步骤以取得良好效果。匹配代价是由具有相似图像强度的邻近像素通过基于交叉的代价聚合的方式组合而成。平滑约束通过半全局匹配进行,同时左右一致性检查被用来检测和消除遮挡区域中的误差。我们进行亚像素增强并应用中值滤波器和双边滤波器以获得最终视差图。
本文的贡献是:
-
基于卷积神经网络的为计算立体匹配代价的两种架构的描述;
-
一种方法,伴随其源代码,在KITTI 2012,KITTI 2015和Middlebury立体视觉数据集中具有最低的错误率;
-
实验分析了数据集大小的重要性,与其他方法相比的错误率,以及不同超参数设置下精度和运行时间之间的权衡。
本文延伸了我们以前的工作(Zbontar和LeCun,2015年),包括一个新架构的描述,两个新数据集的结果,更低的错误率以及更彻底的实验。
2.相关工作
在引入大型立体数据集如KITTI和Middlebury之前,相对较少立体视觉算法使用标签信息来得到他们模型的参数;在这一节,我们回顾一下一些以前的做法。有关立体视觉算法的一般概述,请参阅 Scharstein和Szeliski(2002)。
Kong 和Tao (2004) 采用平方距离的总和来计算初始匹配代价。然后他们训练了一个模型来预测三个类别的概率分布:初始视差正确的,由于前景目标过大导致初始视差不正确的,并且由于其他原因导致初始视差不正确的。预测概率被用来调整初始匹配代价。Kong和Tao(2006)随后延伸了他们的工作,通过组合由计算归一化的不同的窗口大小和中心的互相关获得的预测。Peris等人(2012)用AD- Census(Mei等,2011)进行初始化匹配代价,并使用多类线性判别分析来得知从计算的匹配代价到最终视差的映射。
标签数据还用于得到概率图形模型的参数。Zhang和 Seitz(2007)使用一种替代优化算法来估算马尔科夫随机场超参数的最优值。Scharstein和Pal(2007)构建了一个新的30个立体对的数据集,并使用它来得到条件随机场的参数。Li 和Huttenlocher(2008)提出了一个带非参数代价函数的条件随机场模型,并使用结构化支持向量机来得到模型参数。
最近的工作(Haeusler等人,2013; Spyropoulos等人,2014)集中在估计计算的匹配代价的置信度。Haeusler等人(2013)使用了一种随机森林分类器来组合若干置信度度量方式。同样的,Spyropoulos等人(2014)训练了一个随机森林分类器来预测匹配代价的置信度,并且使用预测结果作为马尔科夫随机场中的软约束来减少立体视觉法的误差。
一个计算匹配代价的相关问题是得到局部图像描述符(Brown等人,2011; Trzcinski等人,2012; Simonyan等人,2014; Revaud等人,2015; Paulin等人,2015;Han等人,2015; Zagoruyko和Komodakis,2015)。这两个问题共享一个公共子任务:测量图像块之间的相似性。Brown等人(2011)提出了一个总体框架来得到图像描述符并使用鲍威尔的方法来选择良好的超参数。为得到局部图像描述符已经提出了几种解决方法,例如Boosting优化(Trzcinski等人,2012),凸优化(Simonyan等人,2014年),分层移动象限的相似性(Revaud等人,2015),卷积内核网络(Paulin等人,2015),和卷积神经网络 (Zagoruyko和Komodakis,2015;Han等人,2015)。Zagoruyko和Komodakis( 2015)的工作,Han等人(2015),特别是,非常类似于我们自己,不同的主要是网络的架构;具体地,包括合并和子采样以考虑更大的块尺寸和更大的视点变化。
3.匹配代价
典型的立体视觉算法首先计算在每个位置p考虑所有视差d的匹配代价。一种计算匹配代价的简单方法是绝对差的总和:
其中,![]() 和
和![]() 是位置p在左右图像中的图像强度,
是位置p在左右图像中的图像强度,![]() 是以P为中心的固定的矩形窗口内的位置集合。
是以P为中心的固定的矩形窗口内的位置集合。
我们使用粗体小写字母p和q表示图像位置。粗体小写d表示向量的视差d,即d=(d,0)。我们为超参数的名称使用typewriter字体。例如,我们将使用patch size字体来表示附近区![]() 的大小
的大小
等式(1)可以理解为测量匹配左图以位置p为中心的图像块与右图以位置p–d为中心的图像块的代价。
我们希望当两个图像块围绕相同的3D点时代价小,反之则代价大。
既然好的和坏的匹配的示例可以从公开可用数据集构建(例如,KITTI和Middlebury立体数据集),我们可以尝试通过监督学习方法来解决匹配问题。受到卷积神经网络在视觉问题中成功应用的启发,我们用它来评估两个小图像块匹配程度。
3.1构造数据集
我们使用来自KITTI或Middlebury立体视觉数据集的地面实况视差图来构建二元分类数据集。在每个真实视差已知的图像位置处,我们提取一个消极的和一个积极的训练示例。这确保了数据集包含相等数量的正例和负例。一个积极的示例是指一对图像块,其中一个来自左边图像,一个来自右边图像,两者的中心像素是同一个3D点,而一个消极的示例是指一对不同于前者的图像块。以下部分详细描述数据集构建步骤。
用![]() 表示一堆像素块,
表示一堆像素块,
Network architectures
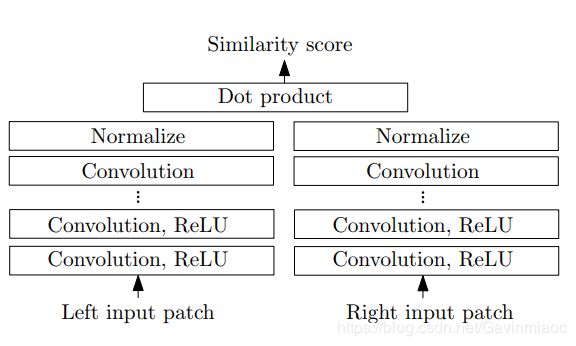
建立两个网络,一个为了速度,一个为了性能。二者输入都是小图像块输出都是它们之间的相似度的测量。二者都用特征提取器来将每个图像块提取成特征向量。块之间相似度是作用在特征向量上而不是原始图像像素强度值上。fast结构是用一个固定的相似性测量,而accurate结构是用一个更好的相似性测量
Fast Architecture
图1 快结构 fast architecture
快结构是一个双塔网络,两个子网络均由一系列的带有Relu的卷积层构成。两个输入块的特征向量之间的余弦cosine相似度作为相似度得分。余弦相似度计算被分为两个步骤:正则规范化和点乘。因为每个位置上面正则规范化只需要运行一次因此这非常节约时间。同时,网络训练的loss是hinge loss(难怪前文强行给样本做成正负样本),loss是根据在图像中同样位置的样本对来计算得到的。这个样本对呢,一个是正样本,一个属于负样本。
![]()
其中S+就是正样本经过网络输出的相似度,S-就是负样本经过网络输出的相似度,m是一个正实数,一般设置成0.2。也就是说当正样本的输出相似度比负样本相似度大的超过m的时候,这个loss会是0,这么看来也是有点道理的!
准确结构 accurate architecture
这个准确网络与快网络最大的不同就是,用一个全连接层来代替余弦相似性度量。这样使得运行时间增加了,但是使得error降低了。同样子网络由很多带Relu的卷积层构成。两个经过特征提取的特征向量会concated然后前向经过很多全连接层(带Relu)。最后一个全连接层会产生一个单独的数字(sigmoid输出),这个数字可以看作输入块的相似性得分。
训练的loss是二元cross-entropy loss(注意与快网络的hinge loss不同),式子就是![]() ,
,
s代表一个训练样本的输出,t代表训练样本的种类,如果样本属于正样本那么t=1,如果样本属于负样本那么就设置成t=0.
那有人要问了,为什么要用两个不同的loss呢,一个原因,经验!而实验告诉我们,cross-entropy loss性能要好于hinge loss,然而,在fast 结构当中,由于我们需要求的是余弦相似计算,所以cross-entropy loss并不直接适用
computing the matching cost
网络的输出是用来初始化matching cost:
P^L(P)与P^R(p-d)是输入块,此刻,并非计算相似性得分而是匹配成本。
既然要计算全部的匹配成本Cnn(p,d)。应该考虑到每个位置以及每个视差。这样的话非常耗时且低效,不过有三条策略让运行时间可控;
1.每个位置值需要对两个子网络的输出计算一次,不需要对每个视差重复计算。
2.两个子网络的输出以图像全分辨率的大小一次性的计算所有的像素。这样只需要进行一次单独的前向,而不是将图片分成若干小块,只在W×H的图像上进行一次前向总比进行wh次前向要快得多。
3.accurate结构中的全连接层的输出也可以仅在一个前向传播中计算。这需要以1×1大小核的卷积层来代替每个全连接层。我们仍然需要考虑每个视差,因此,网络全连接需要运行d次,这就是accurate结构一个瓶颈。
为了计算图像对的匹配成本,对于每个图像运行一次子网络然后运行d次全连接层,其中d就是最大的视差。视野在设计网络结构的时候非常重要。首先,我们应该选择一种结构,接着两个图像concatenated,这确实挺耗时间的,因为整个网络需要运行d次,insight也带来了快结构的进步,其中唯一需要运算d次的是特征向量的dot product。
附:
双目视觉——立体匹配基本理论
双目立体匹配流程详解
立体匹配在英文中叫做Stereo Matching或Stereo Correspondence,但是我没能在wiki上找到Stereo Matching的直接定义,反而简述了Stereo Correspondence,是3D reconstruction的一个重要部分。简单说,立体匹配算法就是要在一对有场景重叠的图片中寻找同名点。在此首先要安利两个立体匹配算法相关的重要网站:
1. KITTI 立体匹配算法排行榜
2. Middlebury 立体匹配算法排行榜
虽然这两个重要的排行榜榜首早已经被深度学习强行占领,但是对于所有学习或研究立体匹配算法的同学来讲,都是一个很好的学习网站, 同时也为大家推荐两篇立体匹配算法相关的综述性文献以及链接:
[1]. Affendi H R , Haidi I . Literature Survey on Stereo Vision Disparity Map Algorithms[J]. Journal of Sensors, 2016, 2016:1-23.
[2]. D. Scharstein and R. Szeliski. A Taxonomy and Evaluation of Dense Two-Frame Stereo Correspondence Algorithms. nternational Journal of Computer Vision, 47(1/2/3):7-42, April-June 2002.
有了这两篇综述性文献,大家肯定能在细细研读后对立体匹配有更为深入的理解和体会。但是,这里需要说明的是,立体匹配算法虽然和特征匹配等技术一样是在两幅图像中寻找同名点,但是他的目标不是要改变两幅图像之间的坐标系统,也不会改变两幅图像之间的坐标系。
参考
1.https://blog.csdn.net/yxq5997/article/details/53700554