前缀和 线段树 树状数组讲解（超详细入门）

博客目录

Part one、前缀和

     引入问题：现输入长度为n的数列co，再输入q个询问，每个询问都给出两个整数l，r。对于每个询问都要求给出对于数列co在区间[l,r]上的和（假设下标从0开始）。

     1. 最直观的方法，就是直接暴力求解，每给出一对l和r，遍历数组co从l到r上所有值并求和。这是初学者最容易想到的方法，但这不是算法爱好者采用的方法，因为它的时间复杂度高达O（n*q），对于n，q<=10 0000来说需要1e10的计算量，时间成本是不可接受的。

      2.前缀和，是懂算法的人比较容易想到的，也是最优的方法。引入一个辅助数组b，大小为n，其中b[i]=co[0]+co[1]+...+co[i]，也就是数列co的前i个元素的和。但是数组b一般不这么算，因为这么算有大量重复计算，复杂度高达O（n*n）。而是采用递推式：

                                                                                   b[i]=b[i-1]+co[i];

公式也不难理解，因为b[i-1]已经是前i-1的和了，再加上co[i]就是所求bi。回到原题，b数组只要一遍初始化，之后对于每个询问L,r，都可以用前缀和来求解：ans=b[r]-b[L-1]，（自己画画图就明白了，离散数学中也有类似的应用），整个题目的时间复杂度降低为O（n+q）。

扩展：

前缀和效率极高，代码简单，但是限制条件比较多。

只要满足 1.数列不变  2.运算结果可以由逆运算一步步还原  3.区间运算求值  一般可以用前缀和求解。

举个例子：

异或运算(xor)结果可以由异或的逆运算（异或的逆运算还是异或）还原得到，即异或的异或还是本身。求区间异或运算值（就是简单地将加法换成异或运算）可以由前缀和计算。

好了，前缀和并不是我们的重点，此处也不另找例子和代码说明了，重点是引入一下两个数据结构：

Part two、线段树

线段树习题和代码：     传送门   <<<<<<<<本篇文章不过多粘贴代码，详情代码请参考此处。

引入习题：

在上面的题目的基础上加一处修改：如果询问的过程中还可以对数组进行修改怎么办？

        现输入长度为n的数列co，再输入q个询问，每个询问给出一个字母x,字母x要么是‘a’，要么是'q'，

        如果是‘a’，则后面会跟三个整数L，r，k，表示给数组co的[L,r]区间上所有元素增加k

        如果是‘q’，则后面会跟两个整数L，r，要求计算数组co区间[L,r]上所有元素和。

        约定数组大小n和询问/修改个数q<=1e5,即不能暴力模拟。

参考题目：hdu1166 敌兵布阵

数据结构简述：

线段树是一个完全二叉树，如下图所示：对于数组2 9 5 8 7 10 4，数组元素作为叶子节点，从左往右每两个叶子求和，作为父亲节点的值，如此递归下去生成根节点的值，即为数组所有元素之和。

一般来说将二叉树放置在sum数组里，空置sum的0号位置不用，root节点放在1位置将二叉树从上到下从左到右依次排列在线性数组中。设父亲节点下标为F，其左孩子下标为L，右孩子下标为R，则有以下关系式：

F=L/2

F=R/2

L=F*2

R=F*2+1

注意：除法向下取整。

（二叉树的的存放和性质，数据结构有讲）

所以，如果可以很容易地找到一个节点x的右孩子的下标：x*2+1；也可以很容易找到一个节点的父亲下标：x/2，根节点没有父亲除外。这样我们就将二叉树存放在了数组里而不破坏二叉树的逻辑形状。

建立操作（build）由递归实现，（请参照：传送门，下同）

基本思想为：想要建立root节点，必须要先建立他的两个孩子节点，要建立孩子节点，必须要先建立孩子的孩子节点，递归直到叶子节点。递归返回的过程，是由叶子节点向上更新所有的祖先的过程，即给所有的祖先加上叶子的值（因为祖先表示了他挂载的所有叶子之和）。

#define lson l , m , rt << 1
#define rson m + 1 , r , rt << 1 | 1
const int maxn = 55555;
int sum[maxn<<2];
void PushUP(int rt){
		sum[rt] = sum[rt<<1] + sum[rt<<1|1];
}
void build(int l,int r,int rt){
	if(l == r){
		scanf("%d",&sum[rt]);
		return;
	}
	int m =(l + r)>>1;
	build(lson);
	build(rson);
	PushUP(rt);
}

查询区间和：对于区间[L,R]，将区间L,R递归分解为若干个节点之和。设当前节点值value表示从A到B上之和，求和方法为sum(L,R，root),由于[L,R]不超过[1,n],从根节点出发，一定可以有[A,B]包含[L,R]，则：

节点左右孩子表示的区间的分界线为：左<=m，右>m，其中m=(A+B)/2

左孩子表示的区间范围为：[A,m],右孩子表示的范围是：[m+1,B]，由父亲节点就能算出当前节点表示范围[A,B]

所以，伪代码：

int sum(L,R,节点){    //节点参数中包含A和B,即当前节点应当表示的区间范围

     令，ret=0，m=(A+B)/2

     如果L<=A 且R>=B 则表示达到了递归终止条件，所以return value;因为递归过程中参数L,R不变，而节点表示的区间范围A和B一直在缩小，直到A和B刚好被L，R包含。

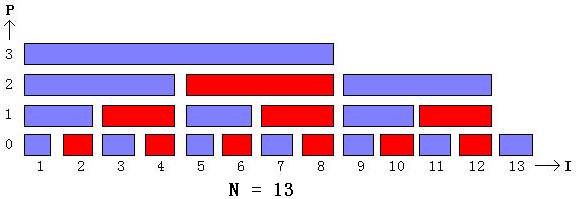
     如果L

     如果R>=m 表示L,R区间有在右孩子上的部分，则ret=ret+sum(L,R,右孩子)

     return ret;

}

int query(int L,int R,int l,int r,int rt){
	if (L <= l && r <= R){
		return sum[rt];
	}
	int m = (l+r)>>1;
	int ret = 0;
	if(L <= m) ret += query(L , R , lson);
	if(R > m) ret += query(L , R , rson);
	return ret;
}

修改操作：首先从root递归找到叶子，然后返回的过程将叶子所有的祖先更新（跟build类似）

void update(int p,int add,int l,int r,int rt){
	if(l == r){
		sum[rt] += add;
		return;
	}
	int m = (l + r) >> 1;
	if(p <= m) update(p , add , lson);
	else update(p , add , rson);
	PushUP(rt);
}

空间复杂度：

     为了保证二叉树能够存下，所以sum数组至少开4*n，

时间复杂度：

     树的建立,由于每个叶子都要向上访问修改所有的祖先（有log（n）个祖先），有n个叶子，所以为O( nlog(n) )

     查询区间和：跟递归深度有关，二叉树的深度最大为log(n),所以为O（logn）

     修改值：与查询类似，要找到叶子并返回跟递归深度有关，所以O(logn)

所以使用线段树的总体时间复杂度为O（nlogn+qlogn），计算量在可接受范围内。

成段更新：

(通常这对初学者来说是一道坎),需要用到延迟标记(或者说懒惰标记),简单来说就是每次更新的时候不要更新到底,用延迟标记使得更新延迟到下次需要查询到的时候。

其实大家把线段树吃透之后知道lazy标记的思想后很容易就自己写出来了，附上博客：
ACM-ICPC 2018 徐州赛区网络预赛  H. Ryuji doesn't want to study —— 线段树lazy标记区间修改

扩展：

各种运算的区间求和，跟线性基结合，求区间最值，求逆序数（逆序数还可以用归并排序求）,etc.

凡是前缀和能解决的问题，线段树都可以解决，线段树比前缀和灵活（主要体现在可修改上），但是代码复杂且需要递归（虽然所有递归都可以手动循环模拟，但是递归是线段树的精髓，不能用递归还是换别的方法吧）

注意：线段树不需要逆运算，而前缀和需要逆运算。所以求区间最值类似的无法逆向的运算不能用前缀和。

而线段树某些功能可以用下面要讲的树状数组更轻量级地实现。

Part Tree、树状数组（Binary Indexed Tree）

树状数组是线段树的轻量版。

一下是一颗二叉树（线段树）的一部分：其中 1~8可看做一颗完整的线段树。横坐标表示数列序号，每个节点（矩形）覆盖的横坐标表示区间范围。用红色标记的矩形均为右孩子。

由前缀和的思想，已知父亲节点表示的区间和F范围为L到R，左孩子表示的区间和C范围为L到M，右孩子表示的区间和为D范围为M到R。我们发现有重复数据：

根据前缀和，由父亲的数据和左孩子的数据，即可算出右孩子的数据：

D=F-C，即右孩子表示的区间和=父亲-左孩子。

所以，我们可以将线段树上所有的右孩子删掉，即将所有红色节点删掉。

这样，第零层叶子节点会被删掉2/n个，第一层双亲节点会被删掉n/4个，第二层双亲节点会被删掉n/8个......

所以只需要n的空间就可以保存剩余的节点。节点和存放位置对应关系如下图 ( 连线表示求和关系）：

大家关注一下不同层次上的节点的序号。

lowbit

设F以二进制表示中最低位的1表示的位权为 lowbit(F) 。注意表示的是位权而不是位置，比如二进制100100中lowbit=4。

第0层（也就是叶子）序号都是奇数（最低位是1）。也就是二进制中位权最低的1在第0位  lowbit=2^0

第1层序号除以2^1（2的一次方）之后是奇数 。      也就是二进制中位权最低的1在第1位    lowbit=2^1

第2层序号除以2^2之后是奇数。                              也就是二进制中位权最低的1在第2位     lowbit=2^2

.......            ......

具体为什么跟二进制有关

其中lowbit函数网上有详细的解释，计算方法和原理如下：

lowbit(x)=x&-x，其中&是按位与。

我们知道计算机内存中负数存放的是补码，由源码到补码的转换为取反加一（符号位不变），也等价为保持最低位的1和1以后（低位的方向）的0不变，将高位所有位取反（符号位不变）。比如11010100变成补码的过程为：保持符号位不变，保持最低位的1和以后的0不变（也就是第三位100不变，最高位1不变），将高位1010取反：0101，最终结果为10101100。负数的补码跟正数有相同的低位（也就是最低位的1和1以后的0），我们所求的lowbit正是相同的低位表示的值。所以只要把相同保留，不同的置0即可。所以这里可以用与运算。当然用与或也可以就是麻烦一点，lowbit(x)=((x^-x)+1)>>1，非主流做法大家一试便知，不做过多解释。

求父亲节点的位置：

设父节点序号为F，它的左孩子节点为L

有结论F=L+lowbit(F) , 相当于加了一个最小的1，即跳转到同层本来应该存在的（但是被删掉的）下一个位置，（同层的加法就是加最低位1的位权，参考上面层数和最低位的1的位置关系）。请大家体会一下。

建立（build）：

同样，保存树的数组（假设为a[]）下标也要从1开始。

需要将数组初始化为0。

与线段树类似的是，读入一个元素之后要更新它所有的祖先，不同的是不需要递归寻找这个元素位置了，因为奇数个元素序号直接就是下标，而偶数个元素直接被删掉了，替换成了节点的元素和之中（不管是第几层的元素和），所以偶数叶子的操作应该是加法。由于数组初始化为0了，所以奇偶个元素的添加都可以统一成加法。添加元素后，需要将改动向上传递，直到传递到root为止。

单点更新

void update(int i, int x){ //i点增量为x
	while(i <= n){
		c[i] += x;
		i += Lowbit(i);
	}
}

建立：

for(i = 1; i <= n; i++){ //i须从1开始
	scanf("%d",&a[i]);
	pushup(i,a[i]);
}

查询区间和：

利用了前缀和的思想求和。

int sum(int x){//区间求和 [1,x]
	int sum=0;
	while(x>0){
		sum+=c[x];//从后面的节点往前加
		x-=Lowbit(x);//同层中向前移动一格，如果遇到L=1的节点会减成0
	}
	return sum;
}
int Getsum(int x1,int x2){ //求任意区间和
	return sum(x2) - sum(x1-1);
}

树状数组的区间修改

参见博客：树状数组 区间修改 区间查询 讲解

小结

前缀和是非常基础的一种方法，效率极高，有很多意想不到的用处，但只能完成非常有限的功能，且需要逆运算。

线段树不需要逆运算。

树状数组是线段树的简化版，能用树状数组实现的一定能用线段树实现，且线段树更加灵活，虽然时间复杂度都一样，但树状数组更加简洁，时间常数更小，空间复杂度常数更小。

但是树状数组对于没有逆运算的运算还是有点不方便。（不是说不能，而是不会，对于我这样的新人来说还是得用线段树）