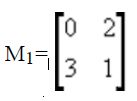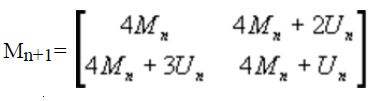GL_DITHER 抖动算法

        对于可用颜色较少的系统，可以以牺牲分辨率为代价，通过颜色值的抖动来增加可用颜色数量。抖动操作是和硬件相关的，OpenGL允许程序员所做的操作就只有打开或关闭抖动操作。实际上，若机器的分辨率已经相当高，激活抖动操作根本就没有任何意义。要激活或取消抖动，可以用glEnable(GL_DITHER)和glDisable(GL_DITHER)函数。默认情况下，抖动是激活的。

抖动算法

应朋友的问题，写一篇解释抖动算法原理的文章。我比较后悔应了朋友的要求，首先自己的水平不高；再次，工作紧张，现在很少时间来研究这个东东。不管怎么样，我总算把这个文章写出来，欢迎朋友们指正批评。

 

朋友的问题侧重彩色图像的抖动，这里，为了解释方便，先说说灰度图像。然后再切入彩色图像的抖动。我在网上看到一篇文章写的很不错，我就拈来贴在这里帮助理解。

 

讲抖动算法，一般都会提到图案法。

图案法(patterning)是指灰度可以用一定比例的黑白点组成的区域表示，从而达到整体图象的灰度感。黑白点的位置选择称为图案化。

 

先岔开说说分辨率，计算机显示器，打印机，扫描仪等设备的一个重要指标就是分辨率，单位是dpi(dot per inch)，即每英寸点数，点数越多，分辨率就越高，图象就越清晰。让我们来计算一下，计算机显示器的分辨率有多高。设显示器为15英寸(指对角线长度)，最多显示1280×1024个点。因为宽高比为4：3，所以宽有12英寸，高有9英寸，则该显示器的水平分辨率为106dpi，垂直分辨率为113.8dpi。一般的激光打印机的分辨率有300dpi×300dpi，600dpi×600dpi，720dpi×720dpi。所以打出来的图象要比计算机显示出来的清晰的多。扫描仪的分辨率要高一些，数码相机的分辨率更高。

 

言归正传，前面讲了，图案化使用图案来表示象素的灰度，那么我们来做一道计算题。假设有一幅240×180×8bit的灰度图，当用分辨率为300dpi×300dpi的激光打印机将其打印到12.8×9.6英寸的纸上时，每个象素的图案有多大？

 

这道题很简单，这张纸最多可以打(300×12.8) ×(300×9.6)=3840×2880个点，所以每个象素可以用(3840/240)×(2880/180)=16×16个点大小的图案来表示，即一个象素256个点。如果这16×16的方块中一个黑点也没有，就可以表示灰度256；有一个黑点，就表示灰度255；依次类推，当都是黑点时，表示灰度0。这样，16×16的方块可以表示257级灰度，比要求的8bit共256级灰度还多了一个。所以上面的那幅图的灰度级别完全能够打印出来。

 

这里有一个图案构成的问题，即黑点打在哪里？比如说，只有一个黑点时，我们可以打在正中央，也可以打16×16的左上角。图案可以是规则的，也可以是不规则的。一般情况下，有规则的图案比随即图案能够避免点的丛集，但有时会导致图象中有明显的线条。

 

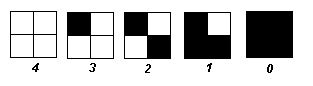
如下图所示，2×2的图案可以表示5级灰度，

 

 

 当图象中有一片灰度为的1的区域时，如下所示，有明显的水平和垂直线条。

 

 

 

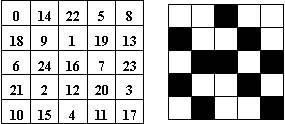
如果想存储256级灰度的图案，就需要256×16×16的二值点阵，占用的空间还是相当可观的。有一个更好的办法是：只存储一个整数矩阵，称为标准图案，其中的每个值从0到255。图象的实际灰度和阵列中的每个值比较，当该值大于等于灰度时，对应点打一黑点。下面举一个25级灰度的例子加以说明。

上图，左边为标准图案，右边为灰度为15的图案，共有10个黑点，15个白点。其实道理很简单，灰度为0时全是黑点，灰度每增加1，减少一个黑点。要注意的是，5×5的图案可以表示26种灰度，当灰度是25才是全白点，而不是灰度为24时。下面介绍一种设计标准图案的算法，是由Limb在1969年提出的。

 

先以一个2×2的矩阵开始：设

通过递归关系有：

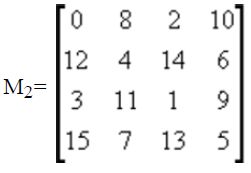
其中Mn和Un均为2n×2n的方阵，Un的所有元素都是1。根据这个算法，可以得到

为16级灰度的标准图案。

M3(8×8阵)比较特殊，称为Bayer抖动表。M4是一个16×16的矩阵。

根据上面的算法，如果利用M3一个象素要用8×8的图案表示，则一幅N×N的图将变成8N×8N大小。如果利用M4，就更不得了，变成16N×16N了。能不能在保持原图大小的情况下利用图案化技术呢？一种很自然的想法是：如果用M2阵，则将原图中每8×8个点中取一点，即重新采样，然后再应用图案化技术，就能够保持原图大
小。实际上，这种方法并不可行。首先，你不知道这8×8个点中找哪一点比较合适，另外，8×8的间隔实在太大了，生成的图象和原图肯定相差很大，就象下图最右边的那幅图一样。

 

我们可以采用这样的做法：假设原图是256级灰度，利用Bayer抖动表，做如下处理

if (g[y][x]>>2) > bayer[y&7][x&7] then 打一白点 else 打一黑点
其中，x,y代表原图的象素坐标，g[y][x]代表该点灰度。首先将灰度右移两位，变成64级，然后将x，y做模8运算，找到Bayer表中的对应点，两者做比较，根据上面给出的判据做处理。
我们可以看到，模8运算使得原图分成了一个个8×8的小块，每个小块和8×8的Bayer表相对应。小块中的每个点都参与了比较，这样就避免了上面提到的选点和块划分过大的问题。模8运算实质上是引入了随机成分，这就是我们下面要讲到的抖动技术。

上图就是利用了这个算法，使用M3(Bayer抖动表)阵得到的；下图是使用M4阵得到的，可见两者的差别并不是很大，所以一般用Bayer表就可以了。

 

 

让我们考虑更坏的情况：即使使用了图案化技术，仍然得不到要求的灰度级别。举例说明：假设有一幅600×450×8bit的灰度图，当用分辨率为300dpi×300dpi的激光打印机将其打印到8×6英寸的纸上时，每个象素可以用(2400/600)×(1800/450)=4×4个点大小的图案来表示，最多能表示17级灰度，无法满足256级灰度的要求。可有两种解决方案：(1)减小图象尺寸，由600×450变为150×113；(2)降低图象灰度级，由256级变成16级。这两种方案都不理想。这时，我们就可以采用“抖动法”(dithering)的技术来解决这个问题。其实刚才给出的算法就是一种抖动算法，称为规则抖动(regular dithering)。规则抖动的优点是算法简单；缺点是图案化有时很明显，这是因为取模运算虽然引入了随机成分，但还是有规律的。另外，点之间进行比较时，只要比标准图案上点的值大就打白点，这种做法并不理想，因为，如果当标准图案点的灰度值本身就很小，而图象中点的灰度只比它大一点儿时，图象中的点更接近黑色，而不是白色。一种更好的方法是将这个误差传播到邻近的象素。

下面介绍的Floyd-Steinberg算法就采用了这种方案。
假设灰度级别的范围从b(black)到w(white)，中间值t为(b+w)/2，对应256级灰度，b=0,w=255,t=127.5。设原图中象素的灰度为g，误差值为e，则新图中对应象素的值用如下的方法得到：
if g > t then
打白点
e=g-w
else
打黑点
e=g-b

3/8 × e 加到右边的象素
3/8 × e 加到下边的象素
1/4 × e 加到右下方的象素
算法的意思很明白：以256级灰度为例，假设一个点的灰度为130，在灰度图中应该是一个灰点。由于一般图象中灰度是连续变化的，相邻象素的灰度值很可能与本象素非常接近，所以该点及周围应该是一片灰色区域。在新图中，130大于128，所以打了白点，但130离真正的白点255还差的比较远，误差e=130-255=-125比较大。将3/8×(-125)加到相邻象素后，使得相邻象素的值接近0而打黑点。下一次，e又变成正的，使得相邻象素的相邻象素打白点，这样一白一黑一白，表现出来刚好就是灰色。如果不传递误差，就是一片白色了。再举个例子，如果一个点的灰度为250，在灰度图中应该是一个白点，该点及周围应该是一片白色区域。在新图中，虽然e=-5也是负的，但其值很小，对相邻象素的影响不大，所以还是能够打出一片白色区域来。这样就验证了算法的正确性。

 

其它的情况你可以自己推敲。下图是利用Floyd-Steinberg算法抖动生成的图。

这里检讨一下，自己虽然是个搞C/C++的，为了偷懒，先用Matlab解决问题……

这里是Matlab的Bayer抖动的算法，用于将256级别的灰度图像抖动成同样尺寸的黑白图片。

clear;
clc;
m1 = [[0 2];[3 1]];
u1=ones(2, 2);
m2=[[4*m1 4*m1+2*u1];[4*m1+3*u1 4*m1+u1]]
u2=ones(4, 4);
m3=[[4*m2 4*m2+2*u2];[4*m2+3*u2 4*m2+u2]]
I = imread('test.bmp');

gI = .2989*I(:,:,1)...
    +.5870*I(:,:,2)...
    +.1140*I(:,:,3);
%imshow(gI);
%r = I(:,:,1);
%g = I(:,:,2);
%b = I(:,:,3);

[h w] = size(gI);

bw = 0;
for i=1:h
    for j=1:w
        if (gI(i,j) / 4> m3(bitand(i, 7) + 1, bitand(j,7) + 1))
            bw(i,j)= 255;
        else
            bw(i,j)= 0;
        end
    end
end
imshow(bw);

 

算法具体思想见《抖动算法小议1》。

这里再说说如何将24bit的真彩色图片变为15bit 或者16bit的图片。还是使用Floyd-steinberg算法。先说说15Bit的组成，红色5bit，绿色5bit，蓝色5bit，1位预留。16Bit的颜色，红、绿、蓝分别是5Bit, 6Bit, 5Bit。这是因为人眼对灰度的感觉比色彩要强，绿色对灰度的贡献最多，所以，多1个bit的绿色量化会使得灰度层次表示更加丰富。

clear;
clc;
I = imread('0001.jpg');
img = double(I);%转换图片
[h w] = size(img(:,:,1));%取得图片的大小


d = 1;%为1时，误差从左传递到右侧，为-1时，误差从右传递到左
re = 0;
ge = 0;
be = 0;
rs = 8;%2^n, n = 3 表示将红色量化等级减少到2^5 = 32种。
gs = 8;%2^n, n = 3 表示将绿色量化等级减少到2^5 = 32种。
bs = 8;%2^n, n = 3 表示将蓝色量化等级减少到2^5 = 32种。
for i=1:h
    for j=1:w
        if (d == 1)
            val = rs * fix(img(i,j,1) / rs);
            re = img(i, j, 1) - val;
            img(i, j, 1) = val;

            val = gs * fix(img(i,j,2) / gs);
            ge = img(i, j, 2) - val;
            img(i, j, 2) = val;

            val = bs * fix(img(i,j,3) / bs);
            be = img(i, j, 3) - val;
            img(i, j, 3) = val;
           
            if ((j + 1) <= w)%计算误差对右侧的像素的传递
                img(i, j + 1, 1) = img(i, j + 1, 1) + re * 3 / 8;
                img(i, j + 1, 2) = img(i, j + 1, 2) + ge * 3 / 8;
                img(i, j + 1, 3) = img(i, j + 1, 3) + be * 3 / 8;
            end
            if ((i + 1) <= h)%计算误差对下侧的像素传递
                img(i + 1, j, 1) = img(i + 1, j, 1) + re * 3 / 8;
                img(i + 1, j, 2) = img(i + 1, j, 2) + ge * 3 / 8;
                img(i + 1, j, 3) = img(i + 1, j, 3) + be * 3 / 8;
            end
            if ((i + 1) <= h && (j + 1) <= w)%计算误差对右下侧的像素传递
                img(i + 1, j + 1, 1) = img(i + 1, j + 1, 1) + re / 4;
                img(i + 1, j + 1, 2) = img(i + 1, j + 1, 2) + ge / 4;
                img(i + 1, j + 1, 3) = img(i + 1, j + 1, 3) + be / 4;
            end
        else
            val = rs * fix(img(i,w - j + 1,1) / rs);
            re = img(i, w - j + 1, 1) - val;
            img(i, w - j + 1, 1) = val;

            val = gs * fix(img(i,w - j + 1,2) / gs);
            ge = img(i, w - j + 1, 2) - val;
            img(i, w - j + 1, 2) = val;

            val = bs * fix(img(i,w - j + 1,3) / bs);
            be = img(i, w - j + 1, 3) - val;
            img(i, w - j + 1, 3) = val;
           
            if ((w - j) > 0)%计算误差对左侧的误差传递
                img(i, w - j, 1) = img(i, w - j, 1) + re * 3 / 8;
                img(i, w - j, 2) = img(i, w - j, 2) + ge * 3 / 8;
                img(i, w - j, 3) = img(i, w - j, 3) + be * 3 / 8;
            end
            if (i + 1 <= h)%计算误差对下侧的像素误差传递
                img(i + 1, j, 1) = img(i + 1, j, 1) + re * 3 / 8;
                img(i + 1, j, 2) = img(i + 1, j, 2) + ge * 3 / 8;
                img(i + 1, j, 3) = img(i + 1, j, 3) + be * 3 / 8;
            end
            if ((i + 1) <= h && (w - j) > 0)%计算误差对左下侧的像素误差传递
                img(i + 1, w - j, 1) = img(i + 1, w - j, 1) + re / 4;
                img(i + 1, w - j, 2) = img(i + 1, w - j, 2) + ge / 4;
                img(i + 1, w - j, 3) = img(i + 1, w - j, 3) + be / 4;
            end
        end
    end
    d = -d;
end
out = uint8(img);
imshow(out)

 

这个是处理的原图片：

 

 

这个是处理后的图片：

如果将24Bit的真彩色图片转换为更低量化级别的图片的时候，其实还是使用Floyd-Steinberg算法，但是直接使用这个算法，效果并不好。原因在于，当颜色特别丰富的图片转换成低彩色的时候，即使用了误差传递，也会因为没有选取合适的颜色表示临近的颜色而产生较大的误差。上篇文章中我们说了24Bit的图片转换为15Bit的图片，颜色的选取，我们看到是直接将 r = r & 0xF8。实际上是直接把图像的低三位信息截去，然后把低三位的信息损失作为误差传递到周围的像素。对于15Bit这样的量化级别，这个方法还是可以接受的。但是对于24Bit的图像变为8Bit，这个算法会产生比较大的误差，并不是Floyd-Steinberg算法的问题，而是颜色选取的不合适，造成了即使有误差传递，图片的失真还是比较大。

 

这里介绍三种颜色选取的办法：

 

• 流行色算法

流行色算法的基本思路是:对彩色图像中所有彩色出现的次数做统计分析，创建一个
数组用于表示颜色和颜色出现频率的统计直方图。按出现频率递减的次序对该直方图数组排序后，直方图中的前256 种颜色就是图像中出现次放最多(频率最大) 的256 种颜色，将它们作为调色板的颜色。该算法用统计直方图来分析颜色出现的频率，因此且称为彩色直方图统计算法。图像中其他的颜色采用在RGB 颜色空间中的最小距离原则映射到与其邻近的256种调色板颜色上。流行色算法实现较简单， 对颜色数量较小的图像可以产生较好的结果，但是该算法存在的主要缺陷是，图像中一些出现频率较低， 但对人眼的视觉效挺明显的信息将丢失。比如，图像中存在的高亮度斑点，由于出现的次数少， 很可能不能被算法选中，将被丢失。

 

• 中位切分算法

 

中位切分算法的基本思路是：在RGB 彩色空间中， R 、G 、B 三基色对所对应于空间的三个坐标轴，将每坐标轴部量化为0 - 255 。对应于最暗(黑) ， 255 对应于最亮，这样就形成了一个边长为256 的彩色立方体。所有可能的颜色都对与立方体内的一个点; 将彩色方体切分成256个小立方体，每个立方体中都包含相同数量的在图像中出现的颜色点；取出每个小立方体的中心点， 则这些点所表示的颜色就是我们所需要的最能代表图像颜色特征的256 种颜色。
中位切分算法是PauJ Heckbert在80 年代初提出来的，现被广泛应用于图像处理领域。该算法的缺点是涉及复杂的排序工作，而且内存开销较大。

 

• 八叉树算法

1988 年，奥地利的M. Gervautz和W. Purgathofer 发表了一篇题为"A Simple Method for Color Quantization: Octree Quantization" 的论文，提出了种新的采用八义树数据结构的颜色量化算法，一般称为八叉树颜色量化算法。该算法的效率比中位切分算法高而且内存开销小。

八叉树颜色量化算法的基本思路是：将图像中使用的RGB 颜色值分布到层状的八叉树中。八叉树的深度可达九层，即根节点层加上分别表示8位的R、G 、B 值的每一位的八层节点。较低的节点层对应于较不重要的RGB 值的位(右边的位) ， 因此， 为了提高效率和节省内存，可以去掉最低部的2 ~ 3 层， 这样不会对结果有太大的影响。叶节点编码存储像素的个数和R 、G 、B 颜色分量的值；而中间的节点组成了从最顶层到叶节点的路径。这是一种高效的存储方式，既可以存储图像中出现的颜色和其出现的次数，也不会浪费内存来存储图像中不出现的颜色。

扫描图像的所有像素， 每遇到种新的颜色就将它放入八叉树中，并创建一个叶节点。图像扫描完后，如果叶子节点的数量大于调色板所需的颜色数时， 就需要将有些叶子节点合并到其上一层节点中， 并将该节点转化成叶节点， 在其中存储颜色且其出现的次数。这样，减少叶节点的数量，直到叶节点的数量等于或小于调色板所需的颜色数。如果叶节点的数量小于或等于调色板所需的颜色数，则可以遍历八叉树，将叶子节点的颜色填入调色饭的颜色表。

 

 

我个人比较推荐八叉树算法，但是还有比八叉树更简单的算法，那就是固定色表的算法。大致思路是：

选取一个比较好的色表为固定色表。然后不管什么图像，每个颜色选取这个色表中值最接近的颜色。这样势必会产生误差，这个误差就可以使用Floyd-Steinberg算法，传递到周围像素，效果也比较好，速度也很快。

 

这个算法的关键就在于如何快速的寻找到色表中最接近的颜色。晕太晚了，下次接着侃……

本文参考资料：

1.OpenGL的帧缓存 

http://blog.csdn.net/skyman_2001/article/details/253954

2.抖动算法小议1、2、3

http://blog.csdn.net/coolbacon/article/details/4041988

http://blog.csdn.net/coolbacon/article/details/4042054

http://blog.csdn.net/coolbacon/article/details/4042122