浅谈自适应滤波器
在通常的滤波场合中,从频域的角度进行滤波,其相关的理论已经相当的成熟,只要给出相应的设计指标就可以很方便的设计出满足要求的滤波器。然而在更一般的情况下,人们所需要的滤波器工作的环境是时变的,这就导致事先已经设计好的滤波器性能下降甚至不能被使用。例如,在水下声纳通信中,信息通过声波在水中进行传播到达接收端,其信道是时变的(这种情况比电磁波在空气中传播要严重的多),如果只是简单的用固定系数的滤波器对信道进行均衡,那么得到的结果往往难以令人满意。解决的办法之一就是利用自适应滤波器,让其时实的跟踪信道的特性然后不断的调整均衡器的参数使其保持在最优的状态。再比如,我们日常使用的扩音设备,如果不注意将麦克风和喇叭靠的太近则会产生令人厌烦的啸叫声,采用自适应滤波技术将能有效的避免这种情况。
自适应滤波器一般是调整固定阶数的横向滤波器(FIR滤波器,当然也有IIR滤波器的,但是这种滤波器自己本身滤波系数设计不当就会导致不稳定,再加上自适应算法的话就更加容易不稳定了,而要想使其变得稳定则需要更加复杂的算法,为了更一般的说明自适应滤波器,故以FIR滤波器为例更适合)的系数来实现自适应滤波,自适应滤波器有两个输入端,分别是横向滤波器输入端信号x(t)、期望信号d(t)。同时也有两个输出端,分别是横向滤波器输出端信号y(t)、误差信号e(t)。下面是它的结构示意图:
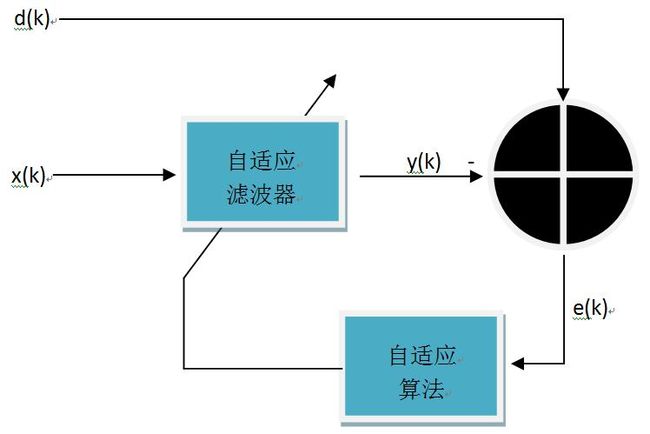
其主要有四大类经典应用包括系统辨识、信道均衡、信号增强和预测等。

系统辨识
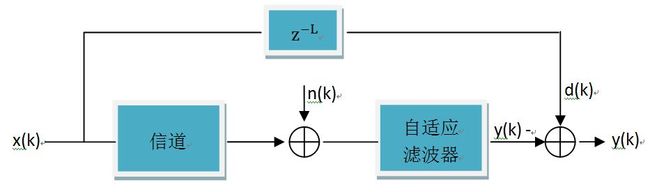
信道均衡
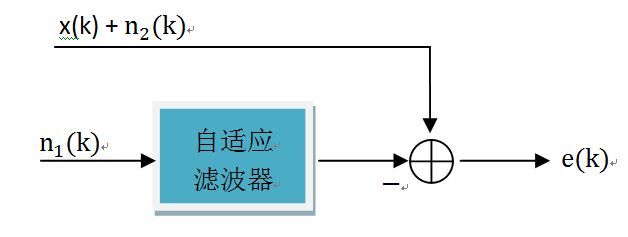
信号增强[其中n1(k)和n2(k)是相关信号]
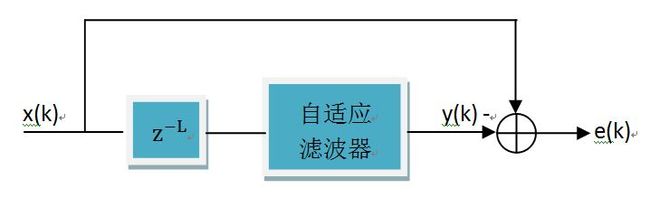
信号预测
关于自适应滤波的算法主要有最小均方误差算法(LMS)和最小二乘算法(RLS),以及它们的各种变形和衍生的算法。下面来分别介绍这两种算法最简单的形式。
最小均方(LMS)误差算法:
最简单的LMS算法是通过每一次迭代输入的数据对当前的目标函数的梯度进行估计,从而得到相应输入信号的自相关矩阵R与互相关向量p。则得到的梯度估计值为:
gw(k) = -2p(k) + 2R(k)w(k) = 2x(k)(-d(k) + w(k)(k)) = -2e(k)x(k)
则滤波系数更新方程为: w(k+1) = w(k) + 2niu*e(k)x(k)
整理可得LMS算法:
初始化部分:
w(k) = [0 0 … 0]T
单次迭代部分:
e(k)= d(k) - w(k)(k)
w(k+1) = w(k) + 2niu*e(k)x(k)
其中niu参数表示单次调节的步长,是一个常数需要在实际的应用中进行确定。我们可以得到单次迭代所需要进行的乘法次数为O[N]量级,N表示FIR滤波器的系数矢量w(k)的维数,该算法已经具有一定的实际应用的价值,如果对滤波的精度要求不是很高,而且对每次迭代速度有很高的要求的话,此算法非常合适。
递归最小二乘(RLS)算法:
在上一节中我们知道,基于瞬时梯度估计的LMS算法实际上只使用了当前时刻的输入信号矢量x(k)和期望信号d(k),没有利用过去的信息这就导致梯度估计的误差很大算法收敛的数度慢,一个很直接的想法就是如果能把过去的信息利用起来,那么梯度估计的误差就会大大的减小,算法很快就会收敛。最小二乘(RL)算法正好就实现了这一过程,它旨在使期望信号与模型滤波器输出之差的平方和最小。具体的算法推导比较的复杂,这里不方便编辑公式同时也没有必要,在这里给出了其算法实现语言描述部分。

下面对其中的一些相关变量名做一下解释,SD(k)表示输入信号矢量的确定性自相关矩阵(RD(k))的逆,e(k)表示先验误差,epsilon(k)表示后验误差(就是图片中的希腊字母epsilon,由于不方便输入所以用它代替了 ,后面还有一个哦 ),lambda表示遗忘因子,意思就是随着时间的推移以前的“旧”的信号对滤波器系数调整的影响越小,主要由更新的数据决定,从这个角度说明了该算法对非平稳的信号也能进行自适应滤波。其它的变量同上。从上面的描述可以看出单次迭代运算量在O[N2]量级,比LMS的计算量要大。
Matlab仿真实验
接下来利用上面的算法进行的Matlab仿真实验,也就是信号增强仿真。首先给出我写的LMS算法m代码:
%递归最小均方算法-----利用瞬时值估计梯度矢量
clc;
clear all;
close all;
%************************生成仿真信号**************************************
Fs = 10000; %设置采样频率
t = 0:1/Fs:7;
t = t';
Size_t = size(t,1);
F1 = 2;
F2 = 10;
F3 = 20;
F4 = 500;
Signal = sin(2*pi*F1*t) + 0.5*sin(2*pi*F2*t) + 0.25*sin(2*pi*F3*t); %生成信号
noise_amp = 1; %定义噪声的标准差
noise1 = noise_amp*randn(Size_t,1); %生成高斯白噪声
noise2 = noise_amp*randn(Size_t,1);
noise3 = 5*sin(2*pi*F4*t+pi/2);
noise = noise2;
Signal_noise = Signal + 0.2*noise; %加入高斯白噪声
Signal_noise(2:end) = Signal_noise(2:end) + 0.15*noise(1:end-1);
Signal_noise(3:end) = Signal_noise(3:end) + 0.1*noise(1:end-2);
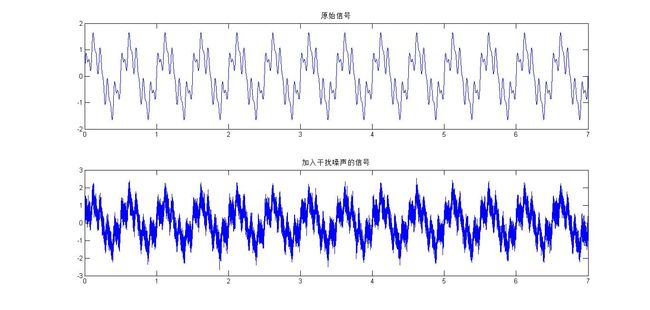
subplot(2,1,1);
plot(t,Signal);
title('原始信号');
subplot(2,1,2);
plot(t,Signal_noise);
title('加入干扰噪声的信号');
%*************************************************************************
M = 3; %定义FIR滤波器阶数
Signal_Len = Size_t - M -1; %定义信号数据的个数
niu = 0.00041; %算法调节步长控制因子
y_out = zeros(Signal_Len,1);
error_out = zeros(Signal_Len,1);
Exp_out = zeros(Signal_Len,1);
w_out = zeros(Signal_Len,M);
for i=1:Signal_Len
%数据输入
if i == 1 %如果是第一次进入
w = zeros(M,1); %初始化滤波器抽头系数
end
d = Signal_noise(i+M-1); %输入新的期望信号
x = noise((M + i -1):-1:i,1); %输入新的信号矢量
%算法正体
y = x' * w; %计算滤波器输出
error = d - y; %计算误差
w_forward = w + niu * error * x; %计算滤波器系数向量
%变量更替
w = w_forward;
%滤波结果存储
y_out(i) = y;
error_out(i) = error;
w_out(i,:) = w';
end
figure;
subplot(2,1,1);
plot(y_out);
title('滤波器输出');
subplot(2,1,2);
plot(error_out);
title('输出误差');
figure;
plot(t(1:Signal_Len),w_out(:,1),'r',t(1:Signal_Len),w_out(:,fix(M/2)+1),'b',t(1:Signal_Len),w_out(:,M),'y');
title('自适应滤波器系数');
下面是实验结果:


可以看到被严重污染的信号经过LMS滤波器得到了不错的恢复。
接下来是给出的是RLS算法的m代码:
%递归最小二乘算法
clc;
clear all;
close all;
%************************生成仿真信号*************************************
Fs = 10000; %设置采样频率
t = 0:1/Fs:3.5;
t = t';
Size_t = size(t,1);
F1 = 2;
F2 = 10;
F3 = 20;
F4 = 1000;
Signal = sin(2*pi*F1*t) + 0.5*sin(2*pi*F2*t) + 0.25*sin(2*pi*F3*t); %生成信号
noise_amp = 1; %定义噪声的标准差
noise1 = noise_amp*randn(Size_t,1); %生成高斯白噪声
noise2 = noise_amp*randn(Size_t,1);
noise3 = 5*sin(2*pi*F4*t+pi/2);
noise = noise2;
Signal_noise = Signal + 0.2*noise; %加入高斯白噪声
Signal_noise(2:end) = Signal_noise(2:end) + 0.15*noise(1:end-1);
Signal_noise(3:end) = Signal_noise(3:end) + 0.1*noise(1:end-2);
subplot(2,1,1);
plot(t,Signal);
title('原始信号');
subplot(2,1,2);
plot(t,Signal_noise);
title('加入干扰噪声的信号');
%*************************************************************************
M = 3; %定义FIR滤波器阶数
lamda = 1; %定义遗忘因子
Signal_Len = Size_t - M -1; %定义信号数据的个数
I = eye(M); %生成对应的单位矩阵
c = 1; %小正数 保证矩阵P非奇异
y_out = zeros(Signal_Len,1);
Eta_out = zeros(Signal_Len,1);
w_out = zeros(Signal_Len,M);
for i=1:Signal_Len
%输入数据
if i == 1 %如果是第一次进入
P_last = I/c;
w_last = zeros(M,1);
end
d = Signal_noise(i+M-1); %输入新的期望信号
x = noise((M + i -1):-1:i,1); %输入新的信号矢量
%算法正体
K = (P_last * x)/(lamda + x'* P_last * x); %计算增益矢量
y = x'* w_last; %计算FIR滤波器输出
Eta = d - y; %计算估计的误差
w = w_last + K * Eta; %计算滤波器系数矢量
P = (I - K * x')* P_last/lamda; %计算误差相关矩阵
%变量更替
P_last = P;
w_last = w;
%滤波结果存储
y_out(i) = y;
Eta_out(i) = Eta;
w_out(i,:) = w';
end
figure;
subplot(2,1,1);
plot(y_out);
title('滤波器输出');
subplot(2,1,2);
plot(Eta_out);
title('输出误差');
figure;
plot(t(1:Signal_Len),w_out(:,1),'r',t(1:Signal_Len),w_out(:,fix(M/2)+1),'b',t(1:Signal_Len),w_out(:,M),'y');
title('自适应滤波器系数');
由于输入的信号与LMS一样故只给出了滤波器输出、输出误差及自适应滤波器系数的结果图,通过对比我们就可以发现RLS算法收敛的速度要比LMS的快多了,而且滤波的质量也比LMS要好。但是计算的时间要比LMS的长。
大概就说这些,还有好多想说的,但这里编辑起来太不方便了,如果有兴趣可以私聊我,我们一起讨论和学习 。我现在只是给出了我研究的一小部分,只是简单的给大家科普了一下。还有关于快速的RLS的算法以及它的稳定算法都没有在上面写出来,除了这些还在TI的TMS320C6678 DSP上用C写了相关的代码,进一步的对代码效率进行了优化。在它上面也进行了仿真并且发现了一些和在Matlab上仿真的不一样的部分。而这个相比于Matlab仿真更加的接近工程实际,更有实用价值。

