树链剖分 讲解+模板+习题
今天我们来讲一下树链剖分
树链剖分是什么?
树链剖分是一种用来维护树上路径信息的在线方法,可以处理在线。
通常通过一种方法,将一棵树剖分成若干条链,然后通过数据结构(线段树,BIT等)去维护。
我们通常所说的树链剖分,基本都是轻重链剖分。
下面我们介绍一下这一种剖分。
学习树链剖分的基础知识有lca,dfs序,线段树等。
首先,我们来明确即可变量。
s i z e i size_i sizei表示以 i i i为子树的大小,包括 i i i
h e a v y i heavy_i heavyi表示 i i i的所有儿子 j j j中 s i z e j size_j sizej最大的一个
连接 i i i和 h e a v y i heavy_i heavyi的边称为重边( h e a v y heavy heavy e d g e s edges edges),其余为轻边( l i g h t light light e d g e s edges edges)
当好多条重边首尾相连,形成了一条更大的重边时,我们称这个重边的集合叫重链( h e a v y heavy heavy p a t h path path)
因为不可能有两条重链相交(根据重链定义可知),所以整棵树被划分成了若干条互不相交的重链。
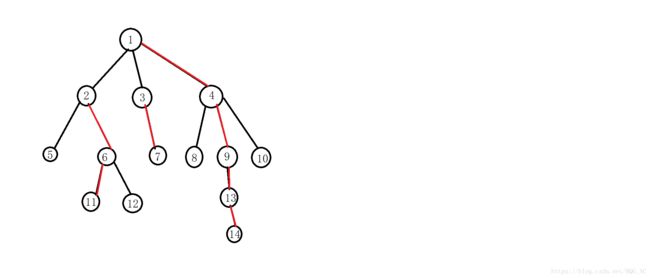
举个例子
红色的边是重边,黑色是轻边。1-2-4-8-16构成了一条重链。
其中所有的重链都不相交
再给一些剖分的性质。
- 每个点只属于一个重链。
- 不可能有两条重链相邻。
- 从一个点开始,重复"重链顶端–>跳一条轻边"这个过程,必定能到根
- 按上述方法跳,必定能在 O ( l o g n ) O(logn) O(logn)步到达顶点。
给一下第4条的证明。
如果一条边是重链,那他一次肯定能跳到重链顶端,这样很快,
而没经过一条轻边,根据重链的定义,轻边所在子树 s i z e size size< 1 2 \frac{1}{2} 21 所有子树 s i z e size size ,则没经过一条轻边,该点得子树大小必定 ∗ 2 *2 ∗2甚至更多,则只会有 O ( l o g n ) O(logn) O(logn)次。
那我们怎么通过代码处理轻重边剖分?
一种经典的处理方法如下。
设
f a t h e r x father_x fatherx表示 x x x的父亲节点
s i z e x size_x sizex表示 x x x的子树大小
d e e p x deep_x deepx表示 x x x的深度
h e a v y x heavy_x heavyx表示 x x x的重儿子
t o p x top_x topx 表示 x x x的重链顶点
处理以上几个数组通常使用两遍dfs处理。
第一次构建前4个数组
第二次本质是对重链进行标号与整理
每次遍历到某点时,先递归它的重儿子,
在递归他的轻儿子,它的重链顶端就是自己
顺便处理 t o p x top_x topx
两遍dfs代码:
void dfs1(int rt){
size[rt]=1;
for (int i=0;i<e[rt].size();i++){
int to=e[rt][i] ;
if (to==fa[rt]) continue ;
fa[to]=rt;dep[to]=dep[rt]+1 ;//信息
dfs1(to) ;
size[rt]+=size[to] ;
if (!hson[rt] || size[to]>size[hson[rt]]) hson[rt]=to ;//处理重儿子
}
}
void dfs2(int rt,int t){
top[rt]=t ;
if (!hson[rt]) return ;
dfs2(hson[rt],t) ;//先递归重儿子
for (int i=0;i<e[rt].size();i++){
int to=e[rt][i] ;
if (to==fa[rt] || to==hson[rt]) continue ;
dfs2(to,to) ;//轻边顶端为自己
}
}
之后,我们用线段树维护每条重链的信息(在实际操作中,轻边也算作重链)
在此同时,我们需要记录每个节点的时间戳 d f n x dfn_x dfnx,同样最好记录每个 d f n x dfn_x dfnx对应的节点,我们用 s e q x seq_x seqx表示。
这两个操作也非常简单,只需在dfs2初始时加这两句话:
dfn[rt]=++tot ;
seq[tot]=rt ;
因为我们是先处理重儿子的,所以重链的节点肯定会被放在线段树的同一个区间中,这样方便线段树操作。
之后上面的剖分过程大体就结束了。
树链剖分能够暴力求出两两点的 l c a lca lca
为何说暴力,因为它不像倍增一样要枚举 2 j 2^j 2j步,他就是每次跳,而且时间复杂度有保障!
我们来讲一讲这个过程。
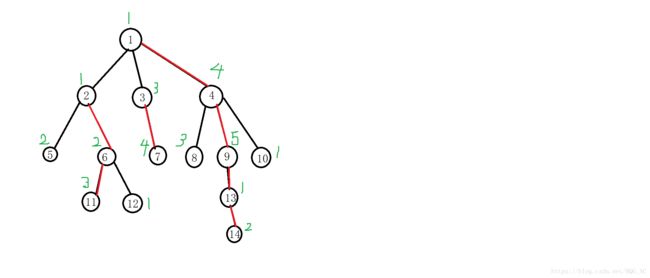
先上一张图
如果要查询9和11的lca,我们手动模拟一下:
1.首先11的dep较大,11跳至1( f a [ t o p [ 11 ] ] fa[top[11]] fa[top[11]])
因为 t o p [ 9 ] = t o p [ 11 ] , top[9]=top[11], top[9]=top[11],所以结束循环,判定深度小的位 l c a lca lca即可
void lca(int x,int y){
int fx=top[x],fy=top[y] ;
while(fx!=fy){
if (dep[x]<dep[y]){ //跳x
swap(x,y) ;
swap(fx,fy) ;
}
x=fa[fx];
fx=top[x] ;
}
if (dep[x]>dep[y]) swap(x,y) ;
return y ;
}
了解了树剖解救lca的过程,基本你已经掌握了树剖了,只差来几道例题,我们不妨讲解几道例题,更深入了解树剖一下。
我们拿BZOJ 1036 树的统计 举个例子。
它让你动态干三件事:
- 把某个点的权值改成t
- 询问x到y的路径上的节点权值的最大值
- 询问x到y的路径上的所以节点权值的和
这是一个树链剖分的裸题。
他让我们动态维护两两点的路径信息。
假设我们剖分写好了,线段树也建好了,我们该怎么求出x到y的路径上的节点权值的最大值和总和呢?
举个例子。
同样是9和11的例子。
11跳到1,我们已经维护2~11的最大值和和,为3和6
之后维护1到9的最大值和和,为5和10
MAX=5 SUM=16
int linkmax(int x,int y){ //链上最大值
int fx=top[x],fy=top[y],ans=-inf ;
while(fx!=fy){
if (dep[fx]<dep[fy]){
swap(x,y) ;
swap(fx,fy) ;
}
ans=max(ans,qmax(1,dfn[fx],dfn[x])) ;
x=fa[fx] ;
fx=top[x] ;
}
if (dep[x]>dep[y]) swap(x,y) ;//在同一条重链上
ans=max(ans,qmax(1,dfn[x],dfn[y])) ;
return ans ;
}
int linksum(int x,int y){ //链上和
int fx=top[x],fy=top[y],ans=0 ;
while(fx!=fy){
if (dep[fx]<dep[fy]){
swap(x,y) ;
swap(fx,fy) ;
}
ans+=qsum(1,dfn[fx],dfn[x]) ;
x=fa[fx] ;
fx=top[x] ;
}
if (dep[x]>dep[y]) swap(x,y) ;
ans+=qsum(1,dfn[x],dfn[y]) ;
return ans ;
}
建议自己手动模拟一下,对于理解算法有很大作用
代码:
#include 一道双倍经验题:【模板】树链剖分
// luogu-judger-enable-o2
#include
int x,y,op ;
int z ;
scanf("%lld",&op);
if (op==1){
scanf("%lld%lld%lld",&x,&y,&z) ;
UPDATE(x,y,z) ;
}
else if (op==2){
scanf("%lld%lld",&x,&y) ;
printf("%lld\n",sum(x,y)) ;
}
else if (op==3){
scanf("%lld%lld",&x,&z) ;
update(dfn[x],dfn[x]+size[x]-1,rt,z) ;
}
else {
scanf("%lld",&x) ;
printf("%lld\n",query(dfn[x],dfn[x]+size[x]-1,rt)) ;
}
}
}
再来一道例题。
BZOJ 4196 NOI2015 软件包管理器
这个问题是动态删链,动态加链的过程。
这题其实比上题还简单,直接维护线段树即可。
#include 都理解了, 来几道习题练练
Aragorn’s Story
[HAOI2015]树上操作
月下“毛景树”
蒟蒻第一次写关于算法的博客,有问题或建议请及时提出,在评论区中发表,博主将及时更改,谢谢阅读!