哈夫曼（Huffman）编码实现

哈夫曼（Huffman）编码实现

哈夫曼编码(Huffman Coding)是一种编码方法，哈夫曼编码是可变字长编码(VLC)的一种。

哈夫曼编码使用变长编码表对源符号（如文件中的一个字母）进行编码，其中变长编码表是通过一种评估来源符号出现机率的方法得到的，出现机率高的字母使用较短的编码，反之出现机率低的则使用较长的编码，这便使编码之后的字符串的平均长度、期望值降低，从而达到无损压缩数据的目的。

哈夫曼编码可以有效的减少编码的长度。

比如你想发送“hello”到朋友那去，hello可以用两位二进制数来表示

h	e	l	o
00	01	10	11

hello可以编码后为0001101011

进行传输，但是这里的l字母出现了两次，出现频率是最高的，于是我们想到可以把出现频率高的字母的编码尽可能的短，那么这样的话，编码长度就会大大缩短了，哈夫曼编码就是为了解决这个问题的

哈夫曼树

哈夫曼编码需要依赖哈夫曼树来实现，哈夫曼树又称为最优二叉树，哈夫曼树是带权路径长度最小的树。

下面逐步介绍如何创建一颗哈夫曼树

假设有这样一串字符 a, b, c, d, e 它们所对应的权重(出现的概率)为 50, 10, 16, 8, 12，现在将它们生成一颗哈夫曼树。

具体过程:
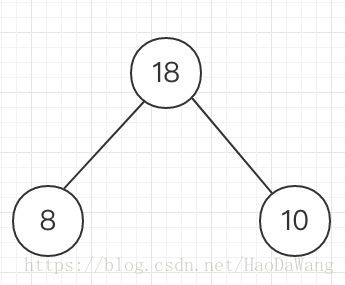
1.先找出权重最小的两个字符构成一棵二叉树，这里最小的为d 和 b

它们父节点的权重是两者相加的结果，现在将b和d的权重从最开始序列( 50, 10, 16, 8, 12)中删除，再将它们的父节点的权重加入，最后为50,16,12,18

重复第一步，直到序列中只有一个元素为止

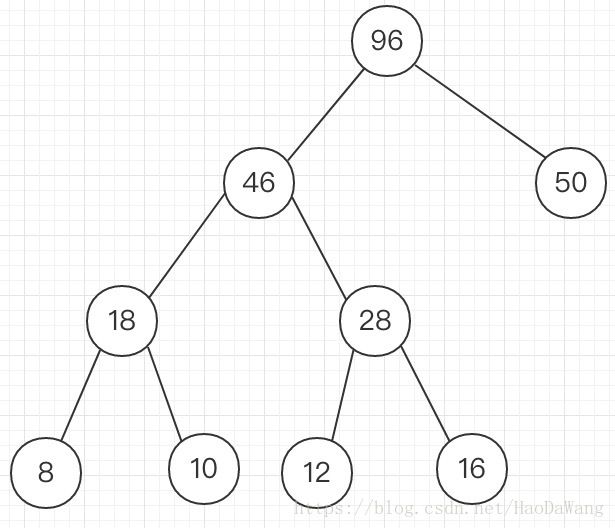
最后生成的哈夫曼树为

从生成的哈夫曼树中可以看出，从根节点到权重最高的字符所需的路径最短。

但如何从哈夫曼树中得到哈夫曼编码呢？只需遵循一个规则：从根节点开始，往下递归寻找，如果是左孩子就为0，右孩子就为1，那么树中的50，也就是a，的哈夫曼编码应该是1，bcde依次是，001，011，000，010

下面给出实现方式（描述语言：js）
ps:为了方便展示，所有的代码都冗到一个文件里了，方便大家看

//节点对象
class HuffmanNode{

    constructor(
        lchild:HuffmanNode,
        rchild:HuffmanNode,
        parent:HuffmanNode,
        data:number
    ){
        this.lchild = lchild
        this.rchild = rchild
        this.parent = parent
        this.data = data
    }

    public lchild:HuffmanNode
    public rchild:HuffmanNode
    public parent:HuffmanNode
    public data:number
}

//复制数组 目的：为了函数的纯度
function copy<T>(arr1:Array):Array<T>{
    let arr2:Array = []
    for(let index in arr1){
        arr2[index] = arr1[index]
    }
    return arr2
}

//创建Huffman树数据序列
function createHuffmanTreeSequence(a:Array):Array<HuffmanNode>{
    let arr = copy(a)
    for(let index in arr){
        arr[index] = new HuffmanNode(null, null, null, arr[index] as number)  
    }
    return arr as Array
}

//寻找容器中最小的结点
function min(arr:Array):HuffmanNode{
    let m:HuffmanNode = arr[0] as HuffmanNode
    for(let val of arr){
        if((val as HuffmanNode).data < m.data) m = val as HuffmanNode
    }
    return m
}

//删除容器中的结点
function remove(arr:Array, index:number){
    arr.splice(index, 1)
}

//创建Huffman树
function createHuffmanTree(a:Array):any{
    let arr = copy(a)
    if(arr.length == 1) {
        return arr[0]
    }

    //寻找容器中最小的两个数
    let val1:HuffmanNode, val2:HuffmanNode
    val1 = min(arr)
    remove(arr, arr.indexOf(val1))
    val2 = min(arr)
    remove(arr, arr.indexOf(val2))

    //父结点
    let parent:HuffmanNode = new HuffmanNode(val1, val2, null, val1.data + val2.data)
    val1.parent = parent
    val2.parent = parent
    arr.push(parent)

    return createHuffmanTree(arr)
}

//Huffman编码
let huffmanEncode = (() => {
    let code:Array = []
    let result:string = ''
    function HuffmanEncode(root:HuffmanNode, char:string, direction:string):void{
        //判断是左孩子还是右孩子
        if(direction == 'left') code.push('0')
        else if(direction == 'right') code.push('1')
        else code = []

        //结点是否存在
        if(!root) return

        //找到值
        if(weightArr[charArr.indexOf(char)] == root.data) {
            result = code.join('')
            return
        }
        HuffmanEncode(root.lchild, char, 'left')
        code.pop()
        HuffmanEncode(root.rchild, char, 'right')
        code.pop()
    }
    return function(root:HuffmanNode, char:string, direction:string):string{
        HuffmanEncode(root, char, direction)
        return result
    }
})()

//字符集
let charArr:Array = ['A','B','C','D','E']
//权重集
let weightArr:Array = [50, 10, 16,8 ,12]
//初始权重数值
let arr:Array = createHuffmanTreeSequence(weightArr)

let huffmanTree:HuffmanNode = createHuffmanTree(arr)

console.log(huffmanEncode(huffmanTree,'E',null)) //010

不懂的地方可以复制到自己的js环境中去试试，这里就不再赘述了