[深度学习基础] 3. 前馈神经网络
1 特征/表示学习
1.1 线性模型上文讨论的 softmax 分类器代表了一系列的线性模型. 它们的训练是凸优化问题, 最终有理论保证能收敛到全局最优, 和参数的初始位置无关. 但是线性分类器只能用多个超平面把输入空间划分为几个简单的区域. 但是对很多问题, 直接把图像原始像素拿去做训练, 线性模型不能将它们分开, 即原始像素不是线性可分的.
针对线性模型要求数据线性可分, 特征工程 (feature engineering) 设计一种最适合当前任务的数据的表示 (representation) φ(x ) 作为输入的特征而不是直接使用原始像素 x , 使得 φ(x) 线性可分. 比如下图, 左图是原始的数据 x , 包括两个类 (红色和蓝色), 每个类的数据各自分布在一个正弦曲线上.
这两类数据不是线性可分的, 线性模型无法将这两类分开. 如果设法设计一种表示 φ(x), 使得数据的分布变成右图那样, 数据将线性可分, 线性模型将能够把这两类分开. SIFT 和 HOG 特征都是特征工程的两个例子.
SIFT 让图像和不同尺度下的高斯滤波器进行卷积, 从得到的图像的差异 (高斯差, DoG) 中找到兴趣点 (一般是 DoG 之后的极大, 极小值点), 以关键点相邻梯度方向分布作为指定方向参数, 使关键点描述拥有旋转不变性. SIFT 寻找可以用来识别目标的局部图像特征, 因此可以用来解决图像中目标有遮挡的情况, 见下图.
HOG 将图像分成小的连通区域, 计算各区域内各像素点的梯度或边缘的方向直方图, 之后把这些直方图组合起来构成图像特征, 见下图. 和SIFT 相似, 两者都利用了图像的局部信息来做识别.
φ( x ) 的设计需要领域的先验知识, 而且和需要解决的任务密切相关. 模型的的性能依赖于数据的表示, 很多情况下, 我们很难设计合适的能应对多种图像识别问题挑战的数据特征, 因此需要大量的工作不断设计更好的特征.
1.3 核方法
在核方法中使用固定的 φ 将 x 映射到一个高维空间, 同时使优化问题仍然保持是凸优化问题. 映射 φ( x ) 使模型的 VC 维 (VC dimension) 提高, 会有潜在的过拟合 (overfitting) 风险. 对 φ(核) 的选取是一种先验知识, 称为核工程 (kernel engineering). 高斯核 (Gaussian kernel)k( x, x ′ ) = exp(−γ∥x - x ′ ∥^2 ) 有十分宽的先验分布, 并且很平滑, 是一种广泛使用的核.
1.4 表示学习
机器学习算法是从数据中学习 (learning from data). 我们能不能利用机器学习算法不仅学习从数据的表示到输出的映射, 也学习到合适的数据的表示呢? 如果学到的表示可以不受光照, 视角等的影响, 反应了数据的本质特征, 这样学到的特征会比人为设计的特征性能更好, 而且这会使 AI 系统有更好的普适性. 从数据中学到合适表示的过程称为表示学习(representation learning). 自编码器 (autoencoder) 就是表示学习的一个例子, 它将输入转化为一个不同的表示.
1.5 深度学习
直接从输入学习到如何提取合适的, 能应对多种图像识别问题挑战的数据的表示 φ 仍然是很难的. 深度学习 (deep learning) 将数据的表示分级, 高级的表示建立在低级的表示上, 机器将从数据简单的表示中学习复杂的表示.
比如在下图中, 直接从原始图像像素中学习到合适的表示是很难的. 深度学习把这样一个复杂的问题分成一系列嵌套的简单的表示学习问题
每个小的表示映射可由神经网络中的一层建模:
• 第一层 φ1 : 从图像的像素和邻近像素的像素值中识别边缘.
• 第二层 φ2 : 将边缘整合起来识别轮廓和角点.
• 第三层 φ3 : 提取特定的轮廓和角点作为输入的特征.
• 最后通过一个线性分类器识别图像中的目标.
这样的一种解决问题的策略称为连接主义 (connectionism). 虽然每一层都是相对简单的运算, 但是多层结合起来会展示出模型强大的力量.
有关经典机器学习, 表示学习, 和深度学习的对比, 见下图, 图中深色的部分代表模型能从数据中学习的部分. 深度学习的具体内容见下文, 本文剩余部分将介绍深度学习的基础—前馈神经网络.
2 假设函数
2.1 数据表示
神经网络中, 上一章讨论的数据驱动过程的各个流程没有改变, 只是在线性分类器中使用的假设函数
里原始图像像素输入 x 变成了可学习的数据的表示 φ(x).
表示 φ( x ) 又由 L − 1 个嵌套的相对简单的表示组成
每个表示 φ_l ( x ) 是由线性运算和非线性运算组成. 最简单的线性运算是仿射(affine) 运算
![]()
其中 W^(l) , b^(l) 是可以从数据中学习到的参数. 非线性运算又称为神经网络中的激活函数 (activation function)
![]()
其中
称为线性整流层单元 (rectified linear units, ReLU, relu). 它将 s 中小于 0 的部分置为 0, 见图4.6. 它将逐元素的应用于 z . 激活函数的作用至关重要. 如果没有激活函数, 多个线性运算的嵌套还是一个线性运算, 因此 h( x ) 仍然是 x 的一个线性运算. 除了 relu 之外, 还有其他的激活函数, 比如 sigmoid函数,
见图. 但是 sigmoid 函数计算比 relu 复杂, 性能也不如 relu, 所以现在除了在 LSTM 中, 已经较少为人使用.
如果令
可将上面的式子用递归的形式简化表示为
其中 W^(L) , b^(L) 是式4.3中的 W, b. a^(L−1) 即是数据的表示 φ( x ). 通过这两式, 即可计算神经网络中的假设函数.
2.2 人工神经元模型
神经网络模型的设计最初是受到生物体内神经元和神经元之间突触连接形式的启发, 见图4.8的左图. 每个神经元 (neuron) 通过树突 (dendrites) 从别的神经元接受信号, 在细胞核 (nucleus) 内处理, 再由轴突 (axon) 将信号传输出去. 轴突在伸出后分叉, 每个又与其他的神经元的树突通过突触(synapses) 相连接.
图中的右图是对生物神经元的一种数学上抽象出来的模型. 神经元通过树突接收到来自其他神经元传来的信号, 这些输入信号通过带权重的连接进行传递, 在细胞核内进行汇总, 然后通过激活函数处理以产生神经元的输出. 如果输入是 x , 权重是 w, 则神经元完成的计算是
如果将 n′ 个神经元堆叠起来, 每个神经元接收同样的输入, 但是每个神经元有各自权重, 神经元之间没有连接, 那么每个神经元的输出
![]()
用向量形式写出来是
2.3 神经网络架构
神经网络的假设函数是
这是一种 L 层的递归形式. 如果每一层都用多个神经元组成, 第 l 层神经元的输出 a^(l) 作为第 l + 1 层神经元的输入, 神经元之间没有同层连接, 相邻层的神经元之间采用全连接, 不存在跨层连接, 这叫做一层全连接层 (fully-connected layer, fc). 这样, 神经网络的假设函数可以用 L 层的全连接层建模, 见图.
注意我们讲一个 L 层神经网络的时候, 是不算输入层的, 因此图中是 3层神经网络. 根据式4.21, 输出层 (第 L 层) 没有激活函数.
3 损失函数
神经网络对应的交叉熵损失函数为
其中
![]()
h( x^(i) ) 是利用式4.21计算得到的.
4 优化
4.1 梯度下降
和在线性分类器中一样, 优化采用的是梯度下降, 参数更新规则是
注意到
因此![]() 和
和![]() 很容易计算.
很容易计算.
但是![]() 和
和![]() , l < L呢? 想要显式的写出
, l < L呢? 想要显式的写出 ![]() 和
和 ![]() 的表达式是非常复杂和困难的.
的表达式是非常复杂和困难的.
4.2 误差反向传播
在第 l 层, 完成的运算是
其中 ⊙ 代表的是逐元素相乘, 即向量的 Hadamard 积 (Hadamard product). 同样的,
只要知道了![]() , 就可以计算
, 就可以计算![]() 和
和![]() 用于更新第 l 层的参数.
用于更新第 l 层的参数. ![]() 传向第 l − 1 层, 用于进一步计算第 l − 1 层的参数的导数. 因此, 从第 l = L 层开始, 应用上面的公式, 直到第 1 层, 就可以计算出所有参数的导数. 这样的算法称为误差反向传播算法 (error back-propagation, BP), 这本质上是微积分中链式求导法则的递归形式的应用.
传向第 l − 1 层, 用于进一步计算第 l − 1 层的参数的导数. 因此, 从第 l = L 层开始, 应用上面的公式, 直到第 1 层, 就可以计算出所有参数的导数. 这样的算法称为误差反向传播算法 (error back-propagation, BP), 这本质上是微积分中链式求导法则的递归形式的应用.
总之, 神经网络的完整训练过程可用下面算法表示.
5 预测和评估
神经网络中的预测和评估方法和线性分类器中的相同, 只不过 s (i) =h( x^(i) ) 是用式4.21计算得到的.
![[深度学习基础] 3. 前馈神经网络_第1张图片](http://img.e-com-net.com/image/info8/e8f33721b5b542d4974a1d071d26ae89.jpg)
![[深度学习基础] 3. 前馈神经网络_第2张图片](http://img.e-com-net.com/image/info8/02d2c07f287640bab3a837b313379190.jpg)
![[深度学习基础] 3. 前馈神经网络_第3张图片](http://img.e-com-net.com/image/info8/9593c6e01c9a44ce8bdece177ad08000.jpg)
![[深度学习基础] 3. 前馈神经网络_第4张图片](http://img.e-com-net.com/image/info8/f92fb10e8538454088cc5464b806bf40.jpg)
![[深度学习基础] 3. 前馈神经网络_第5张图片](http://img.e-com-net.com/image/info8/ca550e8b831b4ec0bbc529c2b8810477.jpg)
![[深度学习基础] 3. 前馈神经网络_第6张图片](http://img.e-com-net.com/image/info8/dc7c04f1aab443329f3dc1f27448f672.jpg)
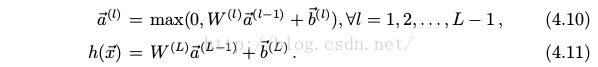
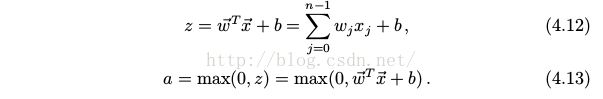
![[深度学习基础] 3. 前馈神经网络_第7张图片](http://img.e-com-net.com/image/info8/b54a21614bd24104bfaf8a482c277900.jpg)
![[深度学习基础] 3. 前馈神经网络_第8张图片](http://img.e-com-net.com/image/info8/404a79ea468247ba8f47542137a9808f.jpg)
![[深度学习基础] 3. 前馈神经网络_第9张图片](http://img.e-com-net.com/image/info8/dc5f2dc43a6f44d1903c104e689fd11d.jpg)
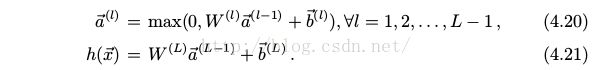
![[深度学习基础] 3. 前馈神经网络_第10张图片](http://img.e-com-net.com/image/info8/05f6301451094d9390bc832fec2ad9eb.jpg)
![[深度学习基础] 3. 前馈神经网络_第11张图片](http://img.e-com-net.com/image/info8/29f66aab6ab34dadafe64644c410fa89.jpg)
![[深度学习基础] 3. 前馈神经网络_第12张图片](http://img.e-com-net.com/image/info8/7f75368cbbf0466c9914ab0e6e6ede19.jpg)
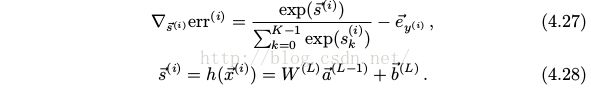
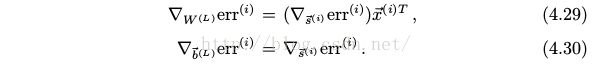
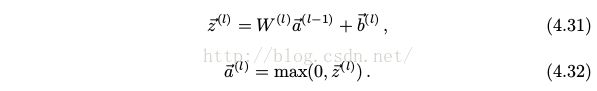
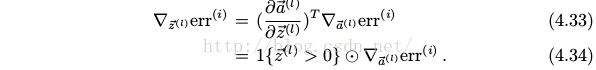
![[深度学习基础] 3. 前馈神经网络_第13张图片](http://img.e-com-net.com/image/info8/77af2965b7d54315a578ab6abb0d2d43.jpg)
![[深度学习基础] 3. 前馈神经网络_第14张图片](http://img.e-com-net.com/image/info8/319fec8fb6c5482ab8b87ab7b73e6a03.jpg)