二分应用

现在我们来学习怎么使用二分。

引用《算法笔记》

1）计算根号2 的近似值。

对于f(x）= x^2来说，在x 属于【1,2】上是单调递增的，这就给我们使用2分法创造了条件。我们可以用以下策略来逼近根号2的值，（根号2 是无理数，所以只能获得它的近似值，我们现在精确到10^-5）

1)如果f(mid) > 根2，说明mid > 根2，应当在【left,mid】中的范围内继续逼近，故令right = mid.

2)如果f(mid) < 根2，说明 mid < 根2，应当在【mid, right】中的范围内继续逼近，故令 left = mid。

上述两步骤当 right - left < 10^-5 时结束，当right - left < 10^-5已经满足要求。mid即为所求近似值。

double f(double x){
	return x * x;
} 
double solve (){
	double left = 1, right = 2;
	double mid;
	while(right - left > 1e-5){
		mid = (left + right)/2;
		if(f(mid) > 2)
			right = mid;
		else
			left = mid;
	}
	return mid;
}

咦我们好像不止可以求 根2 的值，好像还能求很多f（x） = 根x的值，

咦不仅仅是这样，好像只要f(x) 在区间内是个单调的函数，我们都可以利用二分去求f（x） = 0的根

是不是有点晕。

你看下我们求 根2 的值是不是 f(x) = x^2 - 2 = 0 这个函数，（豁然开朗？？？？茅塞顿开？？？）

上个模板？？

const double eps = 1e-5;
double f(double x){
	return ;	//返回值需要看f(x) 上面f(x) = x^2 - 2,那就返回 x * x - 2 
} 
double solve (double L, double R){
	double left = L, right = R;
	double mid;
	while(right - left > 1e-5){
		mid = (left + right)/2;
		if(f(mid) > 0)
			right = mid;
		else
			left = mid;
	}
	return mid;
}

2）装水问题

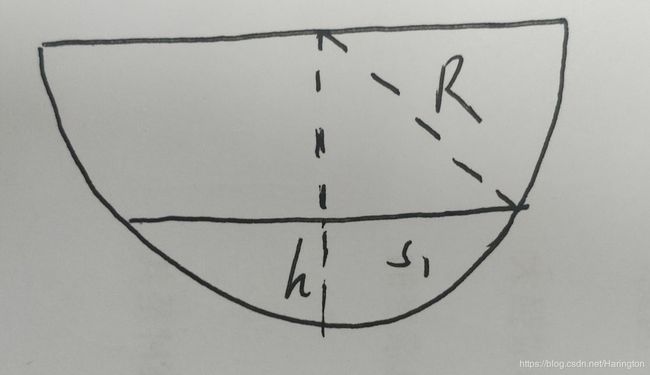
有一个侧面看去是半圆的储水装置，该圆的半径为R，要求往里面装入高度为h的水，使其从侧面看去的面积S1 与半圆面积S2的比例恰好是r, 现在给定R 和 r， 求高度h。

这个思路很好想啊，求一下  半圆面积，求一下s1面积，然后比一下不是r么，能求出来 r和 h 的关系。是一个函数，f(h) = r

但是这个题如果往二分上靠呢？

很显然，随着水面升高，面积比例r一定是增大的。由此可以想到，在[ 0， R]范围内对书面高度h进行二分，计算在高度下面积比例r的值。如果计算的到的r比给定的数值大，说明高度过高，反之则高度低了，这就和2分扯上了关系。

求函数f(h) - r = 0的解。

这题你必须还带有一定的数学基础，

1）扇形区域的面积（那你带会求扇形的角度啊）。

2）这就引申出关于扇形的数学问题，弧长，角度，扇形面积。

角度我们可以用 反余弦公式  acos(x) 函数值的取值范围为 【π， 0】。

扇形面积 = acos(x) * R * R / 2 （原因  ：你可以从整个圆去推，πR*R）

弧长  L = R * acos(x)（也可以用整个圆去推2πR）;

这两个还可以互相推

扇形面积 = （L*R）/ 2;

#include
#include
#include
#include 
#include
using namespace std;
const double PI = acos(-1.0); 
const double eps = 1e-5;

double f(double R, double h){
	double alpha = 2 * acos((R - h) / R);
	double L = 2 * sqrt(R * R - ( R - h )*( R - h));
	double S1 = alpha * R * R / 2 - L * (R - h) / 2;  
	double S2 = PI * R * R / 2;
	return S1 / S2;
} 
double solve (double R, double r){
	double left = 0, right = R;
	double mid;
	while(right - left > 1e-5){
		mid = (left + right)/2;
		if(f(R, mid) > r)
			right = mid;
		else
			left = mid;
	}
	return mid;
}
int main(){
	double R, r;
	scanf("%lf%lf", &R, &r);
	printf("%.4f\n", solve(R, r));
}  

3）木棒切割问题

问题描述：给出N根木棒，长度均已知，现在希望通过切割它们来得到至少K段长度相等（长度为整数）的木棍为这些长度相等的木棒最长能有多长，例如 三根木棍长度分别为 10 ， 24， 15，K = 7，即至少需要7段长度相同的木棍，那么得到的最大长度就为 6， 在这种情况下，第一根木棒提供 1 段， 第2根提供4段， 第3 根提供2 段。达到7段。

我们看题分析，第一 N 个木棒长度，至少分成K 段相等的，那么 当长度上升时 分成的段就会越少（看到这种单调增减的问题），咦是不是能用二分？对于当前长度L来说，我们分成m段 与K比较，如果 m < K 那么我们找的长度长了，如果 m >= K 我们找的长度短了或着正好。那L的取值是什么呢？（肯定是个区间，我认为是【0，n】）这个n是木棒中最长的一根。

继续思考，这不就是求出最后一个满足m >= K 的L的长度，就是求出第一个m  < K 时的L的长度 在 减一就求出了答案

#include
#include
#include
#include 
#include
using namespace std;
int a[105];
int n, k;
int f(int L){
	int ans = 0;
	for(int i = 0; i < n; i++){
		ans += a[i] / L;
	}
	return ans;
}
int solve (int a[], int K){
	int left = 0, right = a[0];
	int mid;
	while(left < right){
		mid = left + (right - left)/2;
		if(f(mid) < K)
			right = mid;
		else
			left = mid + 1;
	}
	return left - 1;
}
int main(){

	
	cin >> n >> k;
	for(int i = 0; i < n; i++)
		cin >> a[i];
	sort(a, a + n);
	cout << solve(a, k) << endl;
}