关键路径 + 拓扑排序

下面关于关键路径的解读分别摘自pigli博客和navorse，我觉得这两者结合起来看，效果会更好，因为两者讲的有的地方详细，有的地方不详细，这样两者结合，就基本全讲详细了

关键路径的算法是建立在拓扑排序的基础之上的，这个算法中用到了拓扑排序，所以在这里先以拓扑排序开篇。

1． 什么是拓扑排序？
举个例子先：一个软件专业的学生学习一系列的课程，其中一些课程必须再学完它的基础的先修课程才能开始。如：在《程序设计基础》和《离散数学》学完之前就不能开始学习《数据结构》。这些先决条件定义了课程之间的领先(优先)关系。这个关系可以用有向图更清楚地表示。图中顶点表示课程，有向边表示先决条件。若课程i是课程j的先决条件，则图中有弧。若要对这个图中的顶点所表示的课程进行拓扑排序的话，那么排序后得到的序列，必须是按照先后关系进行排序，具有领先关系的课程必然排在以它为基础的课程之前，若上例中的《程序设计基础》和《离散数学》必须排在《数据结构》之前。进行了拓扑排序之后的序列，称之为拓扑序列。
2． 如何实现拓扑排序？
很简单，两个步骤：
1． 在有向图中选一个没有前驱的顶点且输出。
2． 从图中删除该顶点和以它为尾的弧。
重复上述两步，直至全部顶点均已输出，或者当前图中不存在无前驱的顶点为止。后一种情况则说明有向图中存在环。
3． 什么是关键路径？

例子开头仍然，图1是一个假想的有11项活动的A0E-网。其中有9个事件v1,v2......，v9，每个事件表示在它之前的活动一完成，在它之后的活动可以开始。如v1表示整个工程的开始，v9表示整个工程结束，v5表示a4和a5已完成，a7和a8可以开始。与每个活动相联系的数是执行该活动所需的时间。比如，活动a1需要6天，a2需要4天。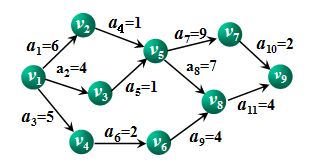

由于整个工程只有一个开始点和一个完成点，故在正常情况(无环)下，网中只有一个入度为零的点(称作源点)和一个出度为零的点(叫做汇点)。
那么该工程待研究的问题是：1.完成整项工程至少需要多少时间？2.哪些活动是影响工程进度的关键？
由于在AOE-网中有些活动可以并行进行，所以完成工程的最短时间是从开始点到完成点的最长路径的长度(这里所说的路径长度是指路径上各活动持续时间之和，不是路径上弧的数目)。路径长度最长的路径叫做关键路径(Critical path)。
假设开始点是v1，从v1到vi的最长路径叫做时间vi的最早发生时间。这个时间决定了所有以vi为尾的弧所表示的活动的最早开始时间。我们用e(i)表示活动ai的最早开始时间。还可以定义一个活动开始的最迟时间l(i)，这是在不推迟整个工程完成的前提下，活动ai最迟必须开始进行的时间。两者之差l(i)-e(i)意味着完成活动ai的时间余量。当这个时间余量等于0的时候，也即是l(i)=e(i)的活动，我们称其为关键活动。显然，关键路径上的所有活动都是关键活动，因此提前完成非关键活动并不能加快工程的进度。
因此，分析关键路径的目的是辨别哪些是关键活动，以便争取提高关键活动的功效，缩短整个工期。

4． 如何实现关键路径？
由上面的分析可知，辨别关键活动就是要找e(i)=l(i)的活动。为了求得e(i)和l(i)，首先应求得事件的最早发生时间ve(j)和最迟发生时间vl(j)。如果活动ai由弧表示，其持续时间记为dut()，则有如下关系
e(i) = ve(j)
l(i) = vl(k) - dut()
求解ve(j)和vl(j)需分两个步进行：
1） 从ve(0)=0开始向前推进求得ve(j)
Ve(j) = Max{ve(i) + dut() };属于T，j=1,2...,n-1
其中T是所有以第j个顶点为头的弧的集合。

2） 从vl(n-1) = ve(n-1)起向后推进求得vl(j)
vl(i) = Min{vl(j) - dut(};属于S，i=n-2,...,0
其中，S是所有以第i个顶点为尾的弧的集合。
这两个递推公式的计算必须分别在拓扑有序和逆拓扑有序的前提先进行。也就是说，ve(j-1)必须在vj的所有前驱的最早发生时间求得之后才能确定，而vl(j-1)必须在Vj的所有后继的最迟发生时间求得之后才能确定。因此可以在拓扑排序的基础上计算ve(j-1)和vl(j-1)。

具体算法描述如下：
1． 输入e条弧，建立AOE-网的存储结构。
2． 拓扑排序，并求得ve[]。从源点V0出发，令ve[0]=0,按拓扑有序求其余各顶点的最早发生时间ve[i]。如果得到的拓扑有序序列中顶点个数小于网中顶点数n，则说明网中存在环，不能求关键路径，算法终止；否则执行步骤3。
3． 拓扑逆序，求得vl[]。从汇点Vn出发，令vl[n-1] = ve[n-1]，按逆拓扑有序求其余各顶点的最迟发生时间vl[i]。
4． 求得关键路径。根据各顶点的ve和vl值，求每条弧s的最早开始时间e(s)和最迟开始时间l(s)。若某条弧满足条件e(s) = l(s)，则为关键活动。

为了能按逆序拓扑有序序列的顺序计算各个顶点的vl值，需记下在拓扑排序的过程中求得的拓扑有序序列，这就需要在拓扑排序算法中，增设一个栈，以记录拓扑有序序列，则在计算求得各顶点的ve值之后，从栈顶到栈底便为逆拓扑有序序列。

进一步解释，上面和下面关于关键路径的解读分别摘自pigli博客和navorse，我觉得这两者结合起来看，效果会更好，因为两者讲的有的地方详细，有的地方不详细，这样两者结合，就基本全讲详细了

AOE网：在一个表示工程的带权有向图中，用顶点表示事件，用有向边表示活动，边上的权值表示活动的持续时间，称这样的有向图叫做边表示活动的网，简称AOE网。AOE网中没有入边的顶点称为始点（或源点），没有出边的顶点称为终点（或汇点）。

AOE网的性质：

⑴ 只有在某顶点所代表的事件发生后，从该顶点出发的各活动才能开始；

⑵ 只有在进入某顶点的各活动都结束，该顶点所代表的事件才能发生。

关键路径：在AOE网中，从始点到终点具有最大路径长度（该路径上的各个活动所持续的时间之和）的路径称为关键路径。

关键活动：关键路径上的活动称为关键活动。关键活动：e[i]=l[i]的活动

　　由于AOE网中的某些活动能够同时进行，故完成整个工程所必须花费的时间应该为始点到终点的最大路径长度。关键路径长度是整个工程所需的最短工期。

与关键活动有关的量：

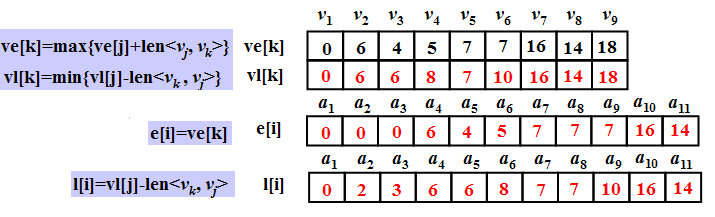
⑴ 事件的最早发生时间ve[k]

　　ve[k]是指从始点开始到顶点vk的最大路径长度。这个长度决定了所有从顶点vk发出的活动能够开工的最早时间。

　　　　

⑵ 事件的最迟发生时间vl[k]

　　vl[k]是指在不推迟整个工期的前提下,事件vk允许的最晚发生时间。

　　　 

 

⑶ 活动的最早开始时间e[i]

　　若活动ai是由弧<vk , vj>表示，则活动ai的最早开始时间应等于事件vk的最早发生时间。因此，有：e[i]=ve[k]

⑷ 活动的最晚开始时间l[i]

　　活动ai的最晚开始时间是指，在不推迟整个工期的前提下， ai必须开始的最晚时间。若ai由弧<vk，vj>表示，则ai的最晚开始时间要保证事件vj的最迟发生时间不拖后。因此，有：l[i]=vl[j]-len<vk, vj>

 

示例：

　　

所以：

下面代码是自己实现的，用的c++，其实也就是用了c++现成的stack而已

代码如下：

#include
#include
#include
#include
#include
#include
#include 

using namespace std;

typedef long long ll;
const int maxm = 20;
const int maxn = 100;
const int inf = 0x3f3f3f3f;
struct node {
	int x, y, w;
	int next;
};
node edge[maxm];
int n, m;
int head[maxn];
//e代表活动开始的最早时间, l活动最迟开始的时间, ve[i]事件最早发生的时间, vl[i]事件最迟发生的时间 ,indegree[i]顶点的入度 
//这个地方没必要分别为e，l开数组了，因为最后只是进行赋值，然后比较两个数是否相等而已，没必要开数组了就，不明白可以看下面的代码 
int e, l, ve[maxn], vl[maxn], indegree[maxn];
stack s, t; //s代表逆序的拓扑排序 ，t代表入度为零的栈，里面存放入度为零的点 

int TopologicalSort() {
	int i, cnt = 0;
	for(i=1; i<=n; ++i) //入度为零的点入栈 
		if(!indegree[i]) {
			t.push(i);
			++cnt;
			//printf("%d ", i);
		}
	while(!t.empty()) {
		int a = t.top();
		s.push(a);
		//printf("%d ", a);
		t.pop();
		//去掉与入度为零的点的相连的边，对应的终点的入度减一 
		int k = head[a];
		while(k != -1) {
			if(!--indegree[edge[k].y]) {//终点的度减一后，如果度为零，入栈 
				t.push(edge[k].y);
				++cnt;
				//printf("%d ", edge[k].y);
			}
			if(ve[edge[k].y] < ve[a] + edge[k].w) //正拓扑排序求事件发生的最早时间ve[i]，到edge[k].y的最长路径 
				ve[edge[k].y] = ve[a] + edge[k].w;
			k = edge[k].next;	
		}
	}
	if(cnt < n) 
		return 0;
	return 1;
}


int main()
{
	int i;
	memset(head, -1, sizeof(head));
	scanf("%d%d", &n, &m);
	
	//建立邻接表 
	for(i=1; i<=m; ++i) {
		scanf("%d%d%d", &edge[i].x, &edge[i].y, &edge[i].w);
		++indegree[edge[i].y];  //终点的入度加一 
		edge[i].next = head[edge[i].x];
		head[edge[i].x] = i;
	}
	
	if(TopologicalSort() == 0) { //在 TopologicalSort()函数里面已经解决了ve的问题 
		printf("不存在关键路径,存在环\n");
		return 0;
	}
	
	memset(vl, inf, sizeof(vl));
	vl[n] = ve[n]; //最后一个事件的最迟发生事件就等于最早发生时间，因为是最后一件事，也就是说这个工程干完了，以后就没有事情做了 
	while(!s.empty()) { //逆拓扑排序求vl[i] 
		int a = s.top();
		s.pop();
		int k = head[a];
		while(k != -1) {
			if(vl[a] > vl[edge[k].y] - edge[k].w) {
				vl[a] = vl[edge[k].y] - edge[k].w;
			}
			k = edge[k].next;
		}
	}
	printf("\n关键活动(该活动不能推迟开工)有:\n");
	for(i=1; i<=n; ++i)  { 
		int k = head[i];
		while(k != -1) {
			e = ve[i]; //该条边的起点代表事情，该条边表示的活动的最早发生时间就等于起点代表的事情的最早发生时间 
			//活动的最迟发生时间
			l = vl[edge[k].y] - edge[k].w;
			if(l == e)
				printf("%d %d %d\n", i, edge[k].y, edge[k].w);
			k = edge[k].next;
		}
	}
	return 0;
}
/*
9 11
1 2 6
1 3 4
1 4 5
2 5 1
3 5 1
4 6 2
5 7 9
5 8 7
6 8 4
7 9 2
8 9 4
*/