手推SVM算法(含SMO证明)
文章目录
- 函数间隔
- 几何间隔
- SVM的目标:最大化几何间隔
- 软间隔
- 核函数
- SMO算法
- 两个变量的选择
- 计算阈值b
- SMO算法总结
- 参考资料:
函数间隔
γ ^ = y ( w T x + b ) = y f ( x ) \hat{\gamma}=y\left(w^{T} x+b\right)=y f(x) γ^=y(wTx+b)=yf(x)
几何间隔
γ ~ = y γ ^ = γ ^ ∥ w ∥ = y ( w T x + b ) ∥ w ∥ \tilde{\gamma}=y \hat{\gamma}=\frac{\hat{\gamma}}{\|w\|} = \frac{y\left(w^{T} x+b\right)}{\|w\|} γ~=yγ^=∥w∥γ^=∥w∥y(wTx+b)
函数间隔可以表示分类预测的正确性及确信度。但是选择分离超平面时,只有函数间隔还不够。因为只要成比例地改变w和 b b b,例如将它们改为 2 w 2w 2w和 2 b 2b 2b,超平面并没有改变,但函数间隔却成为原来的 2 2 2倍。这一事实启示我们,可以对分离超平面的法向量w加某些约束,如规范化, ∣ ∣ w ∣ ∣ = 1 ||w||= 1 ∣∣w∣∣=1,使得间隔是确定的。这时函数间隔成为几何间隔(geometricmargin)。
SVM的目标:最大化几何间隔
SVM的模型是让所有点到超平面的距离大于一定的距离,也就是所有的分类点要在各自类别的支持向量两边。
max y ( w T x + b ) ∥ w ∥ \max\ \frac{y\left(w^{T} x+b\right)}{\|w\|} max ∥w∥y(wTx+b)
s . t . y i ( w T x i + b ) = γ ^ ≥ γ ^ s.t.\ \ y_{i}\left(w^{T} x_{i}+b\right)=\hat{\gamma} \geq \hat{\gamma} s.t. yi(wTxi+b)=γ^≥γ^
一般我们都取函数间隔 γ \gamma γ为1,这样我们的优化函数定义为:
max 1 ∥ w ∥ \max \frac{1}{\|w\|} max∥w∥1
s . t y i ( w T x i + b ) ≥ 1 ( i = 1 , 2 , … m ) { s.t }\ \ y_{i}\left(w^{T} x_{i}+b\right) \geq 1(i=1,2, \ldots m) s.t yi(wTxi+b)≥1(i=1,2,…m)
由于 1 ∥ w ∥ \frac{1}{\|w\|} ∥w∥1的最大化等同于 1 2 ∥ w ∥ 2 \frac{1}{2}{\|w\|}^2 21∥w∥2的最小化。这样SVM的目标函数等价于:
min 1 2 ∥ w ∥ 2 \min \frac{1}{2}{\|w\|}^2 min21∥w∥2
s . t y i ( w T x i + b ) ≥ 1 ( i = 1 , 2 , … m ) { s.t }\ \ y_{i}\left(w^{T} x_{i}+b\right) \geq 1(i=1,2, \ldots m) s.t yi(wTxi+b)≥1(i=1,2,…m)
由于目标函数 min 1 2 ∥ w ∥ 2 \min \frac{1}{2}{\|w\|}^2 min21∥w∥2是凸函数(证明),同时约束条件不等式是仿射的,根据凸优化理论,我们可以通过拉格朗日函数将我们的优化目标转化为无约束的目标函数。优化函数转化为:
L ( w , b , α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 ] L(w, b, \alpha)=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1\right] \qquad \\ L(w,b,α)=21∥w∥2−i=1∑mαi[yi(wTxi+b)−1]
\qquad\qquad\qquad\qquad\qquad\qquad 其中 α i \alpha_i αi为拉格朗日乘子向量,且 α i ≥ 0 \alpha_i \geq0 αi≥0。
根据拉格朗日对偶性,原始问题的对偶问题是极大极小问题:
max α min w , b L ( w , b , α ) \max _{\alpha} \min _{w, b} L(w, b, \alpha) αmaxw,bminL(w,b,α)
为了得到对偶问题的解,需要先求 L ( w , b , α ) L(w,b, \alpha) L(w,b,α)对 w , b w,b w,b的极小,再求对 α \alpha α的极大。
- 求 L ( w , b , α ) L(w,b,α) L(w,b,α)基于 w w w和 b b b的极小值,即 min w , b L ( w , b , α ) \min _{w, b} L(w, b, \alpha) minw,bL(w,b,α),
- 对 w w w和 b b b分别求偏导数得到:
∂ L ∂ w = 0 ⇒ w = ∑ i = 1 m α i y i x i \frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i} ∂w∂L=0⇒w=i=1∑mαiyixi
∂ L ∂ b = 0 ⇒ ∑ i = 1 m α i y i = 0 \frac{\partial L}{\partial b}=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0 ∂b∂L=0⇒i=1∑mαiyi=0
- 带入优化函数 L ( w , b , α ) L(w,b,α) L(w,b,α)消去 w w w
ψ ( α ) = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 ] = 1 2 w T w − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = 1 2 w T ∑ i = 1 m α i y i x i − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = − 1 2 w T ∑ i = 1 m α i y i x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 m α i y i x i T ∑ i = 1 m α i y i x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 m α i y i x i T ∑ i = 1 m α i y i x i + ∑ i = 1 m α i = ∑ i = 1 m α i − 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j \begin{aligned} \psi(\alpha) &=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1\right] \\ &=\frac{1}{2} w^{T} w-\sum_{i=1}^{m} \alpha_{i} y_{i} w^{T} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} b+\sum_{i=1}^{m} \alpha_{i} \\ &=\frac{1}{2} w^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} w^{T} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} b+\sum_{i=1}^{m} \alpha_{i} \\ &=-\frac{1}{2} w^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}-b \sum_{i=1}^{m} \alpha_{i} y_{i}+\sum_{i=1}^{m} \alpha_{i} \\ &=-\frac{1}{2} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}-b \sum_{i=1}^{m} \alpha_{i} y_{i}+\sum_{i=1}^{m} \alpha_{i} \\& =-\frac{1}{2} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}+\sum_{i=1}^{m} \alpha_{i} \\ &=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{aligned} ψ(α)=21∥w∥2−i=1∑mαi[yi(wTxi+b)−1]=21wTw−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=21wTi=1∑mαiyixi−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=−21wTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=−21i=1∑mαiyixiTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=−21i=1∑mαiyixiTi=1∑mαiyixi+i=1∑mαi=i=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
- 求 L ( w , b , α ) L(w,b,α) L(w,b,α)基于 α \alpha α的极大值。
m a x ⎵ α − 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i ∙ x j ) + ∑ i = 1 m α i \underbrace{m a x}_{\alpha}-\frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \bullet x_{j}\right)+\sum_{i=1}^{m} \alpha_{i} α max−21i=1∑mj=1∑mαiαjyiyj(xi∙xj)+i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t. \ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 s.t. i=1∑mαiyi=0
α i ≥ 0 i = 1 , 2 , … m \alpha_{i} \geq 0 i=1,2, \ldots m αi≥0i=1,2,…m
- 可以去掉负号,即为等价的极小化问题如下:
min α 1 2 ∑ i = 1 m ∑ j = 1 m α i α j y i y j ( x i ∙ x j ) − ∑ i = 1 m α i \underset{\alpha}{\min } \frac{1}{2} \sum_{i=1}^{m} \sum_{j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j}\left(x_{i} \bullet x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} αmin21i=1∑mj=1∑mαiαjyiyj(xi∙xj)−i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t. \ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 s.t. i=1∑mαiyi=0
α i ≥ 0 i = 1 , 2 , … m \alpha_{i} \geq 0 i=1,2, \ldots m αi≥0i=1,2,…m
以上是线性分类SVM的硬间隔最大化,下面非线性分类SVM的软间隔最大化
软间隔
SVM对训练集里面的每个样本(xi,yi)引入了一个松弛变量 ξ i ≥ 0 ξ_i≥0 ξi≥0,使函数间隔加上松弛变量大于等于1,也就是说软间隔的约束条件:
y i ( w T x i + b ) ≥ 1 − ξ i y_{i}\left(w^{T} x_{i}+b\right) \geq 1 - \xi_{i} yi(wTxi+b)≥1−ξi
SVM的目标函数变成:
min 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i \min \frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \xi_{i} min21∥w∥2+Ci=1∑mξi
s . t . y i ( w T x i + b ) ≥ 1 − ξ i ( i = 1 , 2 , … m ) s.t.\ y_{i}\left(w^{T} x_{i}+b\right) \geq 1-\xi_{i} \quad(i=1,2, \ldots m) s.t. yi(wTxi+b)≥1−ξi(i=1,2,…m)
ξ i ≥ 0 ( i = 1 , 2 , … m ) \xi_{i} \geq 0 \quad(i=1,2, \dots m) ξi≥0(i=1,2,…m)
求解方法
- 将软间隔最大化的约束问题用拉格朗日函数转化为无约束问题
L ( w , b , ξ , α , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] − ∑ i = 1 m μ i ξ i L(w, b, \xi, \alpha, \mu)=\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \xi_{i}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1+\xi_{i}\right]-\sum_{i=1}^{m} \mu_{i} \xi_{i} L(w,b,ξ,α,μ)=21∥w∥2+Ci=1∑mξi−i=1∑mαi[yi(wTxi+b)−1+ξi]−i=1∑mμiξi
\qquad\qquad\qquad\qquad\qquad\qquad 其中 α i , μ i \alpha_i,\mu_{i} αi,μi为拉格朗日乘子向量,且 α i ≥ 0 , μ i ≥ 0 \alpha_i \geq0,\mu_{i}\geq0 αi≥0,μi≥0。
优化目标也满足KKT条件,通过拉格朗日对偶将我们的优化问题转化为等价的对偶问题来求解
- 求 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ)基于 w w w, ξ \xi ξ, b b b的极小值
- 对 w w w, ξ \xi ξ和 b b b分别求偏导数得到:
∂ L ∂ w = 0 ⇒ w = ∑ i = 1 m α i y i x i \frac{\partial L}{\partial w}=0 \Rightarrow w=\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i} ∂w∂L=0⇒w=i=1∑mαiyixi
∂ L ∂ b = 0 ⇒ ∑ i = 1 m α i y i = 0 \frac{\partial L}{\partial b}=0 \Rightarrow \sum_{i=1}^{m} \alpha_{i} y_{i}=0 ∂b∂L=0⇒i=1∑mαiyi=0
∂ L ∂ ξ = 0 ⇒ C − α i − μ i = 0 \frac{\partial L}{\partial \xi}=0 \Rightarrow C-\alpha_{i}-\mu_{i}=0 ∂ξ∂L=0⇒C−αi−μi=0
- 带入优化函数 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ)消去 w , b w,b w,b
L ( w , b , ξ , α , μ ) = 1 2 ∥ w ∥ 2 + C ∑ i = 1 m ξ i − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] − ∑ i = 1 m μ i ξ i = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 + ξ i ] + ∑ i = 1 m α i ξ i = 1 2 ∥ w ∥ 2 − ∑ i = 1 m α i [ y i ( w T x i + b ) − 1 ] = 1 2 w T w − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = 1 2 w T ∑ i = 1 m α i y i x i − ∑ i = 1 m α i y i w T x i − ∑ i = 1 m α i y i b + ∑ i = 1 m α i = − 1 2 w T ∑ i = 1 m α i y i x i − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ( ∑ i = 1 m α i y i x i ) T ( ∑ i = 1 m α i y i x i ) − b ∑ i = 1 m α i y i + ∑ i = 1 m α i = − 1 2 ∑ i = 1 , j = 1 m α i y i x i T α j y j x j + ∑ i = 1 m α i = ∑ i = 1 m α i − 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j \begin{aligned} L(w, b, \xi, \alpha, \mu) &=\frac{1}{2}\|w\|^{2}+C \sum_{i=1}^{m} \xi_{i}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1+\xi_{i}\right]-\sum_{i=1}^{m} \mu_{i} \xi_{i} \\ &=\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1+\xi_{i}\right]+\sum_{i=1}^{m} \alpha_{i} \xi_{i} \\& =\frac{1}{2}\|w\|^{2}-\sum_{i=1}^{m} \alpha_{i}\left[y_{i}\left(w^{T} x_{i}+b\right)-1\right] \\&=\frac{1}{2} w^{T} w-\sum_{i=1}^{m} \alpha_{i} y_{i} w^{T} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} b+\sum_{i=1}^{m} \alpha_{i} \\&=\frac{1}{2} w^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} w^{T} x_{i}-\sum_{i=1}^{m} \alpha_{i} y_{i} b+\sum_{i=1}^{m} \alpha_{i} \\&=-\frac{1}{2} w^{T} \sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}-b \sum_{i=1}^{m} \alpha_{i} y_{i}+\sum_{i=1}^{m} \alpha_{i} \\&=-\frac{1}{2}\left(\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}\right)^{T}\left(\sum_{i=1}^{m} \alpha_{i} y_{i} x_{i}\right)-b \sum_{i=1}^{m} \alpha_{i} y_{i}+\sum_{i=1}^{m} \alpha_{i} \\&=-\frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} y_{i} x_{i}^{T} \alpha_{j} y_{j} x_{j}+\sum_{i=1}^{m} \alpha_{i} \\&=\sum_{i=1}^{m} \alpha_{i}-\frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j} \end{aligned} L(w,b,ξ,α,μ)=21∥w∥2+Ci=1∑mξi−i=1∑mαi[yi(wTxi+b)−1+ξi]−i=1∑mμiξi=21∥w∥2−i=1∑mαi[yi(wTxi+b)−1+ξi]+i=1∑mαiξi=21∥w∥2−i=1∑mαi[yi(wTxi+b)−1]=21wTw−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=21wTi=1∑mαiyixi−i=1∑mαiyiwTxi−i=1∑mαiyib+i=1∑mαi=−21wTi=1∑mαiyixi−bi=1∑mαiyi+i=1∑mαi=−21(i=1∑mαiyixi)T(i=1∑mαiyixi)−bi=1∑mαiyi+i=1∑mαi=−21i=1,j=1∑mαiyixiTαjyjxj+i=1∑mαi=i=1∑mαi−21i=1,j=1∑mαiαjyiyjxiTxj
- 求 L ( w , b , ξ , α , μ ) L(w, b, \xi, \alpha, \mu) L(w,b,ξ,α,μ)基于 α , μ \alpha,\mu α,μ的极大值,可以去掉负号,即为等价的极小化问题。
min ⎵ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j x i T x j − ∑ i = 1 m α i \underbrace{\min }_{\alpha} \frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} x_{i}^{T} x_{j}-\sum_{i=1}^{m} \alpha_{i} α min21i=1,j=1∑mαiαjyiyjxiTxj−i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t.\ \ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 s.t. i=1∑mαiyi=0
C − α i − μ i = 0 α i ≥ 0 ( i = 1 , 2 , … , m ) μ i ≥ 0 ( i = 1 , 2 , … , m ) } ⇒ 0 ≤ α i ≤ C \left.\begin{matrix} & C-\alpha_{i}-\mu_{i}=0 & \\ & \alpha_{i} \geq 0(i=1,2, \dots, m) & \\ & \mu_{i} \geq 0(i=1,2, \dots, m) & \end{matrix}\right\}\Rightarrow 0 \leq \alpha_{i} \leq C C−αi−μi=0αi≥0(i=1,2,…,m)μi≥0(i=1,2,…,m)⎭⎬⎫⇒0≤αi≤C
核函数
而对于非线性的情况,SVM 的处理方法是选择一个核函数 K ( x , z ) K(x,z) K(x,z) ,通过将数据映射到高维空间,来解决在原始空间中线性不可分的问题。

SVM的目标函数变成:
min ⎵ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j K ( x i , x j ) − ∑ i = 1 m α i \underbrace{\min }_{\alpha} \frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} α min21i=1,j=1∑mαiαjyiyjK(xi,xj)−i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t.\ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 s.t. i=1∑mαiyi=0
0 ≤ α i ≤ C 0 \leq \alpha_{i} \leq C 0≤αi≤C
K ( x i , x j ) = ⟨ ϕ ( x i ) , ϕ ( x j ) ⟩ = ϕ ( x i ) T ϕ ( x j ) K\left(\boldsymbol{x}_{i}, \boldsymbol{x}_{j}\right)=\left\langle\phi\left(\boldsymbol{x}_{i}\right), \phi\left(\boldsymbol{x}_{j}\right)\right\rangle=\phi\left(\boldsymbol{x}_{i}\right)^{\mathrm{T}} \phi\left(\boldsymbol{x}_{j}\right) K(xi,xj)=⟨ϕ(xi),ϕ(xj)⟩=ϕ(xi)Tϕ(xj)
\qquad\qquad\qquad\qquad\qquad\qquad ϕ ( x i ) \phi(x_i) ϕ(xi)为 x x x在低维特征空间到高维特征空间的映射

SMO算法
SMO算法:序列最小最优化(sequential minimal optimization,SMO)算法。
SMO算法要解的问题是一个凸二次规划的对偶问题,变量是拉格朗日乘子,一个变量 α i \alpha_{i} αi对应于一个样本点 ( x i , y i ) (x_i,y_i) (xi,yi);变量的总数等于训练样本容量m。
min ⎵ α 1 2 ∑ i = 1 , j = 1 m α i α j y i y j K ( x i , x j ) − ∑ i = 1 m α i \underbrace{\min }_{\alpha} \frac{1}{2} \sum_{i=1, j=1}^{m} \alpha_{i} \alpha_{j} y_{i} y_{j} K\left(x_{i}, x_{j}\right)-\sum_{i=1}^{m} \alpha_{i} α min21i=1,j=1∑mαiαjyiyjK(xi,xj)−i=1∑mαi
s . t . ∑ i = 1 m α i y i = 0 s.t.\ \sum_{i=1}^{m} \alpha_{i} y_{i}=0 s.t. i=1∑mαiyi=0
0 ≤ α i ≤ C 0 \leq \alpha_{i} \leq C 0≤αi≤C
SMO算法是一种启发式算法,:如果所有变量的解都满足此最优化问题的KKT条件(Karush-Kuhn-Tucker conditions),那么这个最优化问题的解就得到了。因为KKT条件是该最优化问题的充分必要条件。否则,选择两个变量,固定其他变量,针对这两个变量构建一个二次规划问题。这个二次规划问题关于这两个变量的解应该更接近原始二次规划问题的解,因为这会使得原始二次规划问题的目标函数值变得更小。重要的是,这时子问题可以通过解析方法求解,这样就可以大大提高整个算法的计算速度。子问题有两个变量,一个是违反KKT条件最严重的那一个,另一个由约束条件自动确定。如此,SMO算法将原问题不断分解为子问题并对子问题求解,进而达到求解原问题的目的。
- 选择变量 α 1 , α 2 \alpha_1,\alpha_2 α1,α2,固定 α 3 , α 4 , … , α m \alpha_{3}, \alpha_{4}, \dots, \alpha_{m} α3,α4,…,αm,目标函数变为:
min α 1 , α 1 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 α 1 ∑ i = 3 m y i α i K i 1 + y 2 α 2 ∑ i = 3 m y i α i K i 2 \underset{\alpha_{1}, \alpha_{1}}{\min } \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2}-\left(\alpha_{1}+\alpha_{2}\right)+y_{1} \alpha_{1} \sum_{i=3}^{m} y_{i} \alpha_{i} K_{i 1}+y_{2} \alpha_{2} \sum_{i=3}^{m} y_{i} \alpha_{i} K_{i 2} α1,α1min21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1α1i=3∑myiαiKi1+y2α2i=3∑myiαiKi2
s . t . α 1 y 1 + α 2 y 2 = − ∑ i = 3 m y i α i = ζ s.t. \ \ \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{m} y_{i} \alpha_{i}=\zeta s.t. α1y1+α2y2=−i=3∑myiαi=ζ
0 ≤ α i ≤ C i = 1 , 2 0 \leq \alpha_{i} \leq C\qquad i=1,2 0≤αi≤Ci=1,2
- 分析约束条件,所有的 α 1 , α 2 \alpha_1,\alpha_2 α1,α2都要满足约束条件,且 y 1 , y 2 y_1,y_2 y1,y2均只能取值1或者-1,然后在约束条件下求最小。
α 1 y 1 + α 2 y 2 = − ∑ i = 3 m y i α i = ζ \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{m} y_{i} \alpha_{i}=\zeta α1y1+α2y2=−i=3∑myiαi=ζ
0 ≤ α i ≤ C i = 1 , 2 0 \leq \alpha_{i} \leq C\qquad i=1,2 0≤αi≤Ci=1,2
有四种情况,画出图形分析(横轴为 α 1 \alpha_1 α1,纵轴为 α 2 \alpha_2 α2):
s . t . α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ s.t.\ \ \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta s.t. α1y1+α2y2=−i=3∑Nyiαi=ζ
0 ≤ α 1 ≤ C , 0 ≤ α 2 ≤ C , 0 \leq \alpha_{1} \leq C,0 \leq \alpha_{2} \leq C, 0≤α1≤C,0≤α2≤C,
- 情况一: y 1 = 1 , y 2 = 1 , α 1 + α 2 = ζ y_1 = 1,y_2 =1,\alpha_1+ \alpha_2 = \zeta y1=1,y2=1,α1+α2=ζ
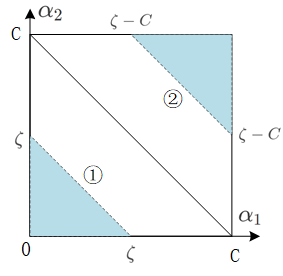
① 0 < ζ < C : 0 ≤ α 1 ≤ ζ , 0 ≤ α 2 ≤ ζ 0<\zeta<C:0 \leq \alpha_{1} \leq \zeta,0 \leq \alpha_{2} \leq\zeta 0<ζ<C:0≤α1≤ζ,0≤α2≤ζ.
② c < ζ < 2 C : ζ − C ≤ α 1 ≤ C , ζ − C ≤ α 2 ≤ C c<\zeta<2C:\zeta-C \leq \alpha_1\leq C,\zeta-C \leq \alpha_2\leq C c<ζ<2C:ζ−C≤α1≤C,ζ−C≤α2≤C
将 α 2 o l d + α 1 o l d = ζ \alpha_{2}^{o l d}+\alpha_{1}^{o l d} = \zeta α2old+α1old=ζ代入①,②得:
0 ≤ α 2 ≤ α 1 old + α 2 old α 1 old + α 2 old − C ≤ α 2 ≤ C } \left.\begin{matrix} & 0 \leq \alpha_{2} \leq \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }}& \\ & \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }} -C\leq \alpha_2 \leq C& \end{matrix}\right\} 0≤α2≤α1 old +α2 old α1 old +α2 old −C≤α2≤C}
⇒ max ( 0 , α 2 o l d + α 1 o l d − C ) ≤ α 2 ≤ min ( C , α 2 o l d + α 1 o l d ) \Rightarrow \max \left(0, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}-C\right) \leq \alpha_2 \leq \min \left(C, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}\right) ⇒max(0,α2old+α1old−C)≤α2≤min(C,α2old+α1old)
- 情况二: y 1 = − 1 , y 2 = − 1 , α 1 + α 2 = − ζ y_1 =-1,y_2 =-1,\alpha_1+ \alpha_2 =- \zeta y1=−1,y2=−1,α1+α2=−ζ
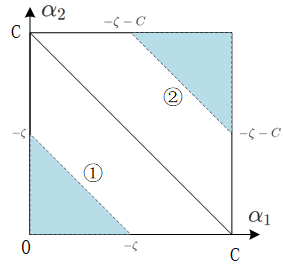
① 0 < − ζ < C : 0 ≤ α 1 ≤ − ζ , 0 ≤ α 2 ≤ − ζ 0<-\zeta<C:0 \leq \alpha_{1} \leq - \zeta,0 \leq \alpha_{2} \leq - \zeta 0<−ζ<C:0≤α1≤−ζ,0≤α2≤−ζ.
② c < − ζ < 2 C : − ζ − C ≤ α 1 ≤ C , − ζ − C ≤ α 2 ≤ C c<-\zeta<2C:-\zeta-C \leq \alpha_1\leq C, - \zeta-C \leq \alpha_2\leq C c<−ζ<2C:−ζ−C≤α1≤C,−ζ−C≤α2≤C
将 α 2 o l d + α 1 o l d = − ζ \alpha_{2}^{o l d}+\alpha_{1}^{o l d} = -\zeta α2old+α1old=−ζ代入①,②得:
0 ≤ α 2 ≤ α 1 old + α 2 old α 1 old + α 2 old − C ≤ α 2 ≤ C } \left.\begin{matrix} & 0 \leq \alpha_{2} \leq \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }}& \\ & \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }} -C\leq \alpha_2 \leq C& \end{matrix}\right\} 0≤α2≤α1 old +α2 old α1 old +α2 old −C≤α2≤C}
⇒ max ( 0 , α 2 o l d + α 1 o l d − C ) ≤ α 2 ≤ min ( C , α 2 o l d + α 1 o l d ) \Rightarrow \max \left(0, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}-C\right) \leq \alpha_2 \leq \min \left(C, \alpha_{2}^{o l d}+\alpha_{1}^{o l d}\right) ⇒max(0,α2old+α1old−C)≤α2≤min(C,α2old+α1old)
- 情况三: y 1 = 1 , y 2 = − 1 , α 1 − α 2 = ζ y_1 = 1,y_2 =-1,\alpha_1- \alpha_2 = \zeta y1=1,y2=−1,α1−α2=ζ
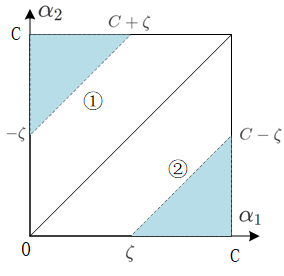
① 0 < − ζ < C : 0 ≤ α 1 ≤ C + ζ , − ζ ≤ α 2 ≤ C 0<-\zeta<C:0 \leq \alpha_{1} \leq C+ \zeta,- \zeta \leq \alpha_{2} \leq C 0<−ζ<C:0≤α1≤C+ζ,−ζ≤α2≤C.
② 0 < ζ < C : ζ ≤ α 1 ≤ C , 0 ≤ α 2 ≤ C − ζ 0<\zeta<C:\zeta \leq \alpha_1\leq C, 0 \leq \alpha_2\leq C- \zeta 0<ζ<C:ζ≤α1≤C,0≤α2≤C−ζ
将 α 2 o l d + α 1 o l d = − ζ \alpha_{2}^{o l d}+\alpha_{1}^{o l d} = -\zeta α2old+α1old=−ζ代入①,②得:
0 ≤ α 2 ≤ α 1 old + α 2 old α 1 old + α 2 old − C ≤ α 2 ≤ C } \left.\begin{matrix} & 0 \leq \alpha_{2} \leq \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }}& \\ & \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }} -C\leq \alpha_2 \leq C& \end{matrix}\right\} 0≤α2≤α1 old +α2 old α1 old +α2 old −C≤α2≤C}
⇒ max ( 0 , α 2 o l d − α 1 o l d ) ≤ α 2 ≤ min ( C , α 2 o l d − α 1 o l d + C ) \Rightarrow \max \left(0, \alpha_{2}^{o l d}-\alpha_{1}^{o l d}\right) \leq \alpha_2 \leq \min \left(C, \alpha_{2}^{o l d}-\alpha_{1}^{o l d} + C \right) ⇒max(0,α2old−α1old)≤α2≤min(C,α2old−α1old+C)
- 情况四: y 1 = − 1 , y 2 = 1 , α 1 + α 2 = − ζ y_1 =-1,y_2 =1,\alpha_1+ \alpha_2 = - \zeta y1=−1,y2=1,α1+α2=−ζ
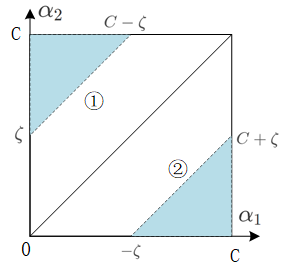
① 0 < ζ < C : 0 ≤ α 1 ≤ C − ζ , ζ ≤ α 2 ≤ C 0<\zeta<C:0 \leq \alpha_{1} \leq C- \zeta,\zeta \leq \alpha_{2} \leq C 0<ζ<C:0≤α1≤C−ζ,ζ≤α2≤C.
② 0 < − ζ < C : − ζ ≤ α 1 ≤ C , 0 ≤ α 2 ≤ C + ζ 0<-\zeta<C:-\zeta \leq \alpha_1\leq C, 0 \leq \alpha_2\leq C + \zeta 0<−ζ<C:−ζ≤α1≤C,0≤α2≤C+ζ
将 α 2 o l d − α 1 o l d = − ζ \alpha_{2}^{o l d}-\alpha_{1}^{o l d} = -\zeta α2old−α1old=−ζ代入①,②得:
0 ≤ α 2 ≤ α 1 old + α 2 old α 1 old + α 2 old − C ≤ α 2 ≤ C } \left.\begin{matrix} & 0 \leq \alpha_{2} \leq \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }}& \\ & \alpha_{1}^{\text { old }}+\alpha_{2}^{\text { old }} -C\leq \alpha_2 \leq C& \end{matrix}\right\} 0≤α2≤α1 old +α2 old α1 old +α2 old −C≤α2≤C}
⇒ max ( 0 , α 2 o l d − α 1 o l d ) ≤ α 2 ≤ min ( C , α 2 o l d − α 1 o l d + C ) \Rightarrow \max \left(0, \alpha_{2}^{o l d}-\alpha_{1}^{o l d}\right) \leq \alpha_2 \leq \min \left(C, \alpha_{2}^{o l d}-\alpha_{1}^{o l d} + C \right) ⇒max(0,α2old−α1old)≤α2≤min(C,α2old−α1old+C)
假设最初的可行解为 α 2 o l d , α 1 o l d \alpha_{2}^{o l d},\alpha_{1}^{o l d} α2old,α1old,最优解为 α 2 n e w , α 1 n e w \alpha_{2}^{new},\alpha_{1}^{new} α2new,α1new,并且假设在沿着约束方向未经剪辑时 α 2 \alpha_2 α2的最优解为 α 2 n e w , u n c \alpha_{2}^{new,unc} α2new,unc。由于 α 2 new \alpha_{2}^{\text { new }} α2 new 满足 0 ⩽ α i ⩽ C 0 \leqslant \alpha_{i} \leqslant C 0⩽αi⩽C,所以,最优值 α 2 n e w \alpha_{2}^{new} α2new的取值范围必须满足条件:
L ⩽ α 2 n e w ⩽ H L \leqslant \alpha_{2}^{\mathrm{new}} \leqslant H L⩽α2new⩽H
若 y 1 = y 2 y_1 = y_2 y1=y2:
L = max ( 0 , α 2 old + α 1 old − C ) , H = min ( C , α 2 old + α 1 old ) L=\max \left(0, \alpha_{2}^{\text { old }}+\alpha_{1}^{\text { old }}-C\right), \quad H=\min \left(C, \alpha_{2}^{\text { old }}+\alpha_{1}^{\text { old }}\right) L=max(0,α2 old +α1 old −C),H=min(C,α2 old +α1 old )
若 y 1 ! = y 2 y_1 != y_2 y1!=y2:
L = max ( 0 , α 2 old − α 1 old ) , H = min ( C , C + α 2 old − α 1 old ) L=\max \left(0, \alpha_{2}^{\text { old }}-\alpha_{1}^{\text { old }}\right), \quad H=\min \left(C, C+\alpha_{2}^{\text { old }}-\alpha_{1}^{\text { old }}\right) L=max(0,α2 old −α1 old ),H=min(C,C+α2 old −α1 old )
最终的 α 2 n e w \alpha_2^{new} α2new为:
α 2 n e w = { H α 2 n e w , u n c > H α 2 n e w , u n c L ≤ α 2 n e w , u n c ≤ H L α 2 n e w , u n c < L \alpha_{2}^{n e w}=\left\{\begin{array}{ll}{H} & {\alpha_{2}^{n e w, u n c}>H} \\ {\alpha_{2}^{n e w, u n c}} & {L \leq \alpha_{2}^{n e w, u n c} \leq H} \\ {L} & {\alpha_{2}^{n e w, u n c}<L}\end{array}\right. α2new=⎩⎨⎧Hα2new,uncLα2new,unc>HL≤α2new,unc≤Hα2new,unc<L
无约束时 α 2 n e w , u n c 的 解 : \alpha_{2}^{n e w, u n c}的解: α2new,unc的解:
α 2 new, unc = α 2 old + y 2 ( E 1 − E 2 ) η \alpha_{2}^{\text { new, unc }}=\alpha_{2}^{\text { old }}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta} α2 new, unc =α2 old +ηy2(E1−E2)
其中:
η = K 11 + K 22 − 2 K 12 = ∥ Φ ( x 1 ) − Φ ( x 2 ) ∥ 2 \eta=K_{11}+K_{22}-2 K_{12}=\left\|\Phi\left(x_{1}\right)-\Phi\left(x_{2}\right)\right\|^{2} η=K11+K22−2K12=∥Φ(x1)−Φ(x2)∥2
Φ ( x ) \Phi(\mathrm{x}) Φ(x)是输入空间到特征空间的映射。
E i E_i Ei为函数 g ( x ) g(x) g(x)对输入 x i x_i xi的预测值与真实输出 y i y_i yi之差。
g ( x ) = ∑ i = 1 N α i y i K ( x i , x ) + b g(x)=\sum_{i=1}^{N} \alpha_{i} y_{i} K\left(x_{i}, x\right)+b g(x)=i=1∑NαiyiK(xi,x)+b
E i = g ( x i ) − y i = ( ∑ j = 1 N α j y j K ( x j , x i ) + b ) − y i i = 1 , 2 E_{i}=g\left(x_{i}\right)-y_{i}=\left(\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{j}, x_{i}\right)+b\right)-y_{i} \quad i=1,2 Ei=g(xi)−yi=(j=1∑NαjyjK(xj,xi)+b)−yii=1,2
证明 α 2 n e w , u n c \alpha_{2}^{n e w, u n c} α2new,unc的解:
引进记号
v i = ∑ j = 3 N α j y j K ( x i , x j ) = g ( x i ) − ∑ j = 1 2 α j y j K ( x i , x j ) − b i = 1 , 2 v_{i}=\sum_{j=3}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)=g\left(x_{i}\right)-\sum_{j=1}^{2} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)-b \quad i=1,2 vi=j=3∑NαjyjK(xi,xj)=g(xi)−j=1∑2αjyjK(xi,xj)−bi=1,2
目标函数 W ( α 1 , α 2 ) W(\alpha_1,\alpha_2) W(α1,α2)可写成:
W ( α 1 , α 2 ) = 1 2 K 11 α 1 2 + 1 2 K 22 α 2 2 + y 1 y 2 K 12 α 1 α 2 − ( α 1 + α 2 ) + y 1 v 1 α 1 + y 2 v 2 α 2 \begin{aligned} W\left(\alpha_{1}, \alpha_{2}\right)=& \frac{1}{2} K_{11} \alpha_{1}^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{1} y_{2} K_{12} \alpha_{1} \alpha_{2} \\ &-\left(\alpha_{1}+\alpha_{2}\right)+y_{1} v_{1} \alpha_{1}+y_{2} v_{2} \alpha_{2} \end{aligned} W(α1,α2)=21K11α12+21K22α22+y1y2K12α1α2−(α1+α2)+y1v1α1+y2v2α2
因为:
α 1 y 1 = ζ − α 2 y 2 \mathrm{\alpha}_{1} \mathrm{y}_{1}=\zeta-\mathrm{\alpha}_{2} \mathrm{y}_{2} α1y1=ζ−α2y2
y i 2 = 1 y_{i}^{2}=1 yi2=1
所以:
α 1 = ( ζ − y 2 α 2 ) y 1 \alpha_{1}=\left(\zeta-y_{2} \alpha_{2}\right) y_{1} α1=(ζ−y2α2)y1
将 α 1 \alpha_1 α1代入 W ( α 1 , α 2 ) W(\alpha_1,\alpha_2) W(α1,α2),得到只含有 α 2 \alpha_2 α2的函数的目标函数
W ( α 2 ) = 1 2 K 11 ( ζ − α 2 y 2 ) 2 + 1 2 K 22 α 2 2 + y 2 K 12 ( ζ − α 2 y 2 ) α 2 − ( ζ − α 2 y 2 ) y 1 − α 2 + v 1 ( ζ − α 2 y 2 ) + y 2 v 2 α 2 \begin{aligned} W\left(\alpha_{2}\right)=& \frac{1}{2} K_{11}\left(\zeta-\alpha_{2} y_{2}\right)^{2}+\frac{1}{2} K_{22} \alpha_{2}^{2}+y_{2} K_{12}\left(\zeta-\alpha_{2} y_{2}\right) \alpha_{2} \\ &-\left(\zeta-\alpha_{2} y_{2}\right) y_{1}-\alpha_{2}+v_{1}\left(\zeta-\alpha_{2} y_{2}\right)+y_{2} v_{2} \alpha_{2} \end{aligned} W(α2)=21K11(ζ−α2y2)2+21K22α22+y2K12(ζ−α2y2)α2−(ζ−α2y2)y1−α2+v1(ζ−α2y2)+y2v2α2
对 α 2 \alpha_2 α2求导数:
( K 11 + K 22 − 2 K 12 ) α 2 = y 2 ( y 2 − y 1 + ζ K 11 − ζ K 12 + v 1 − v 2 ) = y 2 [ y 2 − y 1 + ζ K 11 − ζ K 12 + ( g ( x 1 ) − ∑ j = 1 2 y j α j K 1 j − b ) − ( g ( x 2 ) − ∑ j = 1 2 y j α j K 2 j − b ) ] \begin{aligned}\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}=& y_{2}\left(y_{2}-y_{1}+\zeta K_{11}-\zeta K_{12}+v_{1}-v_{2}\right) \\=& y_{2}\left[y_{2}-y_{1}+\zeta K_{11}-\zeta K_{12}+\left(g\left(x_{1}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{1 j}-b\right)\right.\\ &-\left(g\left(x_{2}\right)-\sum_{j=1}^{2} y_{j} \alpha_{j} K_{2 j}-b\right) ] \end{aligned} (K11+K22−2K12)α2==y2(y2−y1+ζK11−ζK12+v1−v2)y2[y2−y1+ζK11−ζK12+(g(x1)−j=1∑2yjαjK1j−b)−(g(x2)−j=1∑2yjαjK2j−b)]
将 ζ = α 1 old y 1 + α 2 old y 2 \zeta=\alpha_{1}^{\text { old }} \mathrm{y}_{1}+\alpha_{2}^{\text { old }} \mathrm{y}_{2} ζ=α1 old y1+α2 old y2代入,得到:
( K 11 + K 22 − 2 K 12 ) α 2 new, unc = y 2 ( ( K 11 + K 22 − 2 K 12 ) α 2 old y 2 + y 2 − y 2 − y ( x 1 ) − g ( x 2 ) ) = ( K 11 + K 22 − 2 K 12 ) α 2 old + y 2 ( E 1 − E 2 ) \begin{aligned}\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text { new, unc }} &=y_{2}\left(\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text { old }} y_{2}+y_{2}-y_{2}-y\left(x_{1}\right)-g\left(x_{2}\right)\right) \\ &=\left(K_{11}+K_{22}-2 K_{12}\right) \alpha_{2}^{\text { old }}+y_{2}\left(E_{1}-E_{2}\right) \end{aligned} (K11+K22−2K12)α2 new, unc =y2((K11+K22−2K12)α2 old y2+y2−y2−y(x1)−g(x2))=(K11+K22−2K12)α2 old +y2(E1−E2)
将 η = K 11 + K 22 − 2 K 12 \eta=\mathrm{K}_{11}+\mathrm{K}_{22}-2 \mathrm{K}_{12} η=K11+K22−2K12代入,得到:
α 2 n e w , u n c = α 2 o l d + y 2 ( E 1 − E 2 ) η \alpha_{2}^{\mathrm{new}, \mathrm{unc}}=\alpha_{2}^{\mathrm{old}}+\frac{y_{2}\left(E_{1}-E_{2}\right)}{\eta} α2new,unc=α2old+ηy2(E1−E2)
要使其满足不等式约束必须将其限制在区间 [ L , H ] [\mathrm{L}, \mathrm{H}] [L,H],从而得到 α 2 n e w \alpha_{2}^{\mathrm{new}} α2new的表达式,由于 α 1 y 1 + α 2 y 2 = − ∑ i = 3 N y i α i = ζ \alpha_{1} y_{1}+\alpha_{2} y_{2}=-\sum_{i=3}^{N} y_{i} \alpha_{i}=\zeta α1y1+α2y2=−∑i=3Nyiαi=ζ,从而得到 α 1 new = α 1 old + y 1 y 2 ( α 2 old − α 2 new ) \alpha_{1}^{\text { new }}=\alpha_{1}^{\text { old }}+y_{1} y_{2}\left(\alpha_{2}^{\text { old }}-\alpha_{2}^{\text { new }}\right) α1 new =α1 old +y1y2(α2 old −α2 new )。
两个变量的选择
SMO算法在每个子问题中选择两个变量优化,其中至少一个变量是违反KKT条件的。
-
第1个变量的选择(外层循环):
- 违背KKT条件最严重的样本点,即:检验训练样本点 ( x i , y i ) (x_i,y_i) (xi,yi)是否满足KKT条件。
α i = 0 ⇔ y i g ( x i ) ⩾ 1 0 < α i < C ⇔ y i g ( x i ) = 1 α i = C ⇔ y i g ( x i ) ⩽ 1 \begin{array}{c}{\alpha_{i}=0 \Leftrightarrow y_{i} g\left(x_{i}\right) \geqslant 1} \\ {0<\alpha_{i}<C \Leftrightarrow y_{i} g\left(x_{i}\right)=1} \\ {\alpha_{i}=C \Leftrightarrow y_{i} g\left(x_{i}\right) \leqslant 1}\end{array} αi=0⇔yig(xi)⩾10<αi<C⇔yig(xi)=1αi=C⇔yig(xi)⩽1
其中: g ( x i ) = ∑ j = 1 N α j y j K ( x i , x j ) + b g\left(x_{i}\right)=\sum_{j=1}^{N} \alpha_{j} y_{j} K\left(x_{i}, x_{j}\right)+b g(xi)=j=1∑NαjyjK(xi,xj)+b
在检验过程中,外层循环首先遍历所有满足条件 0 < α i < C 0<\alpha_{i}<C 0<αi<C的样本点,即在间隔边界上的支持向量点,检验它们是否满足KKT条件。如果这些样本点都满足KKT条件,那么遍历整个训练集,检验它们是否满足KKT条件。 - 违背KKT条件最严重的样本点,即:检验训练样本点 ( x i , y i ) (x_i,y_i) (xi,yi)是否满足KKT条件。
-
第1个变量的选择(内层循环)
- 希望能使第二个变量有足够大的变化,即最大化 ∣ E 1 − E 2 ∣ \left|\mathrm{E}_{1}-\mathrm{E}_{2}\right| ∣E1−E2∣。此外,为了节省计算时间,将所有 E i E_i Ei值保存在一个列表中。
- 如果内层循环通过以上方法选择的 α 2 \alpha_2 α2不能使目标函数有足够的下降,那么采用以下启发式规则继续选择 α 2 \alpha_2 α2。遍历在间隔边界上的支持向量点,依次将其对应的变量作为 α 2 \alpha_2 α2试用,直到目标函数有足够的下降。若找不到合适的 α 2 \alpha_2 α2,那么遍历训练数据集;若仍找不到合适的 α 2 \alpha_2 α2,则放弃第1个 α 1 \alpha_1 α1,再通过外层循环寻求另外的 α 1 \alpha_1 α1。
计算阈值b
-
当 0 < α 1 n e w < C 0<\alpha_{1}^{n e w}<C 0<α1new<C时:
由KKT条件:
∑ i = 1 N α i y i K i 1 + b = y 1 \sum_{i=1}^{N} \alpha_{i} y_{i} K_{i 1}+b=y_{1} i=1∑NαiyiKi1+b=y1
得: b 1 n e w = y 1 − ∑ i = 3 N α i y i K i 1 − α 1 n e w y 1 K 11 − α 2 n a w y 2 K 21 b_{1}^{\mathrm{new}}=y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}-\alpha_{1}^{\mathrm{new}} y_{1} K_{11}-\alpha_{2}^{\mathrm{naw}} y_{2} K_{21} b1new=y1−i=3∑NαiyiKi1−α1newy1K11−α2nawy2K21
又: E 1 = ∑ i = 3 N α i y i K i 1 + α 1 old y 1 K 11 + α 2 old y 2 K 21 + b old − y 1 E_{1}=\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}+\alpha_{1}^{\text { old }} y_{1} K_{11}+\alpha_{2}^{\text { old }} y_{2} K_{21}+b^{\text { old }}-y_{1} E1=i=3∑NαiyiKi1+α1 old y1K11+α2 old y2K21+b old −y1
所以: y 1 − ∑ i = 3 N α i y i K i 1 = − E 1 + α 1 old y 1 K 11 + α 2 old y 2 K 21 + b old y_{1}-\sum_{i=3}^{N} \alpha_{i} y_{i} K_{i 1}=-E_{1}+\alpha_{1}^{\text { old }} y_{1} K_{11}+\alpha_{2}^{\text { old }} y_{2} K_{21}+b^{\text { old }} y1−i=3∑NαiyiKi1=−E1+α1 old y1K11+α2 old y2K21+b old
因此:
b 1 n e w = − E 1 − y 1 K 11 ( α 1 n e w − α 1 o l d ) − y 2 K 21 ( α 2 n e w − α 2 o l d ) + b o l d b_{1}^{\mathrm{new}}=-E_{1}-y_{1} K_{11}\left(\alpha_{1}^{\mathrm{new}}-\alpha_{1}^{\mathrm{old}}\right)-y_{2} K_{21}\left(\alpha_{2}^{\mathrm{new}}-\alpha_{2}^{\mathrm{old}}\right)+b^{\mathrm{old}} b1new=−E1−y1K11(α1new−α1old)−y2K21(α2new−α2old)+bold -
当 0 < α 2 n e w < C 0<\alpha_{2}^{n e w}<C 0<α2new<C时:
b 2 n e w = − E 2 − y 1 K 12 ( α 1 n e w − α 1 o l d ) − y 2 K 22 ( α 2 n e w − α 2 o l d ) + b o l d b_{2}^{n e w}=-E_{2}-y_{1} K_{12}\left(\alpha_{1}^{n e w}-\alpha_{1}^{o l d}\right)-y_{2} K_{22}\left(\alpha_{2}^{n e w}-\alpha_{2}^{o l d}\right)+b^{o l d} b2new=−E2−y1K12(α1new−α1old)−y2K22(α2new−α2old)+bold
最终的 b 2 n e w b_{2}^{n e w} b2new为:
b n e w = b 1 n e w + b 2 n e w 2 b^{n e w}=\frac{b_{1}^{n e w}+b_{2}^{n e w}}{2} bnew=2b1new+b2new -
更新 E i E_i Ei
E i = ∑ S y j α j K ( x i , x j ) + b n e w − y i E_{i}=\sum_{S} y_{j} \alpha_{j} K\left(x_{i}, x_{j}\right)+b^{n e w}-y_{i} Ei=S∑yjαjK(xi,xj)+bnew−yi
其中,S是所有支持向量 x j x_j xj的集合。
SMO算法总结
输入: 训练数据集 T = { ( x 1 , y 1 ) , ( x 2 , y 2 ) , … , ( x N , y N ) } \mathrm{T}=\left\{\left(\mathrm{x}_{1}, \mathrm{y}_{1}\right),\left(\mathrm{x}_{2}, \mathrm{y}_{2}\right), \ldots,\left(\mathrm{x}_{\mathrm{N}}, \mathrm{y}_{\mathrm{N}}\right)\right\} T={(x1,y1),(x2,y2),…,(xN,yN)},其中x为n维特征向量,y为二元输出,值为1,或者-1.精度e
输出:近似解α
- 取初值 α 0 = 0 , k = 0 \alpha^{0}=0, k=0 α0