chapter-3-损失函数和优化

损失函数

上一章我们了解了线性分类器的函数形式:f(x,W) = x * W +b。

有时候我们想了解它的分类性能，为此我们定义了损失函数(loss function，也称目标函数或代价函数)：

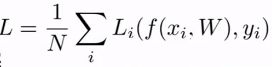
其中N是输入数据的数量，yi是我们理想的结果向量。例如，对一个共有3类的数据集，属于第一类的数据的yi为(1,0,0)T。Li是单个数据的损失函数，L为所有输入数据的损失函数的平均值。通过这一方式，我们就能定量的描述W和b的好坏。

这里Li的计算方式为：枚举每一个错误分类的值与正确分类的差，再用这个值加上设定好的安全边界值。若和小于等于0，则该错误分类的损失为0；否则损失即为和。计算每个错误分类的损失并求和，记为该分类的损失。

如下图为例，猫的损失函数值为(设安全边距为1)：
max(5.1 + 1 - 3.2,0) + max((-1.7) + 1 - 3.2,0) = max(0 , 2.9) + max(0 , -3.9) = 2.9 。

而汽车的损失函数为0，青蛙的损失为12.9。总的损失即为(2.9 + 0 + 12.9) / 3 = 5.3。

这种损失函数由于其函数图像的样子，也被称为折页损失函数：

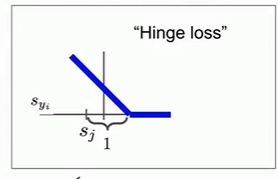
其横轴为数据正确分类的值，纵轴为损失。

上述是一个损失函数的实例，但在实际应用时，我们要根据算法的特点、我们关心的误差类型，来选择恰当的误差函数。

关于损失函数，还有一个问题：有时候程序为了在训练时得到最好的结果，可能会得到过于复杂的权重和偏置。然而一般来说，这样的分类器在测试集上运行时效果会较差。

基于这一原因以及奥卡姆剃刀的思想(“如非必要，勿增实体”).，我们在损失函数中引入一个正则项：λR(W)。

这里的λ是一个超参数，也就是说它需要在程序运行前被指定。

而R(W)的计算方式由很多，常见的有以下几种：

还有一个常用的损失函数是多项式逻辑回归(multinomial logistic regression,也称为Softmax)。其计算方式是，对某一输入数据，分别计算其各个分类结果的自然指数值，并对结果归一化。然后计算其正确分类对应的值的-ln()值。实例如下：

这两种损失函数有一个差异在于：当你使用折页损失函数时，如果你对数据的分类性能达到了设定的要求，那么后续分类效果即使进一步提升，也不能够体现出来。而Softmax函数则不同，它会随着分类效果的提升，持续降低函数值，直到值降为0为止。

优化

上节介绍了评估W的好坏程度的方法，那么问题来了，如何得到更好的W呢？

想象你在一个大的山谷中散步，山谷中的每个点都对应于W的一个设置带来的损失，而你的工作是找到这个山谷的最低点。

以下是几种方法：

一：

随机选取W的值，并计算其对应的损失函数值，直到其为0为之。但在实践中这种方法非常愚蠢。

二：

或许你可以跟随坡度的变化寻找最低点。只要每次都朝向当前坡度变化最大的方向前进，我们就可以逐渐抵达山谷的最低点。对应于函数，即使选择梯度最大的方向改变W。一个实例如下：

对W的第一个值进行微小的改变，并计算改变后的损失值，然后计算其梯度。然后恢复原样，计算下一个值，直到计算完所有的值。然后我们选择梯度最小所对应的变化，保存这种变化。直到分类器的性能已经足够好。

详细的介绍可见：https://blog.csdn.net/JachinMa/article/details/90147263

梯度下降算法虽然非常好，但当处理大型数据时，它要一次次地进行迭代和计算，所需要的算力开销会非常大。为了改进它，我们提出了随机梯度下降算法。

随机梯度算法不需要计算整个训练集的误差的梯度，而是在每次迭代时，随机选取一部分训练样本，称为小批量(minibatch)。一般选取的数量是2的指数，然后我们使用这样本来计算损失及梯度。

图像特征

有时候直接将图像数据全部输入程序，效果会很差。为了解决这个问题，我们采取了这样的方法：首先计算图像的各种特征，然后将不同的特征向量聚合到一起，得到其特征表述。将特征表述作为输入数据，输入程序。

以下是一个体现这种做法好处的例子：

我们很难设计出一个线性分类器来分类左边的图像，但如果对其转换，得到转换特征，就可以得到较容易使用线性分类器分类的右边的图像。

下面是一个特征的例子：

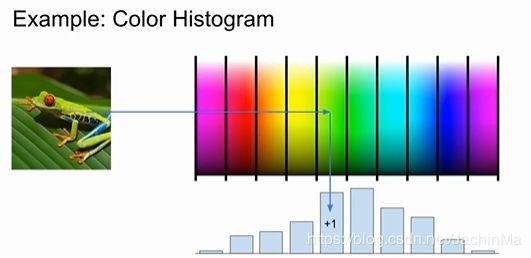
对一幅图片，我们可以得到其颜色图谱，并计算每类图谱的出现次数，得到对应的直方图，也就是一个特征向量。

还有一个特征的例子是方向直方图：

另外一个特征是词袋：

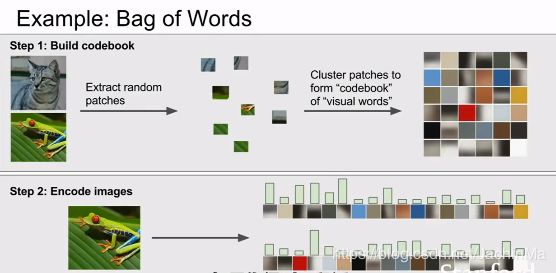
如果你得到一段话，用一个特征向量来表示这段话的一种方法是：统计每个词出现的次数。这也可以应用于图像。

我们可以利用k-均值这样的算法，首先随机选取几个像素作为簇中心，最后得到数个聚类。我们可以将每个聚类视作语句种的单词，进而对其进行计数，得到特征向量。