chapter-7-训练神经网络(下)

更好的优化方法

当损失在一些方向敏感，而在其他方向不敏感的话，更新线效率会很低。另一个问题是在鞍点或局部最低点时，会让函数卡住。还有一个问题是SGD的随机性：当处在噪音环境下时，SGD的随机性会是使计算速度大幅下降。

为了改善上述问题，我们引入了动量项：

它是保持一个时间变化的速度，并且将梯度估计添加到这个速度上，然后在这个速度的方向上步进。

在速度上还有一个表示摩擦系数的超参数来对速度进行衰减。
于是，当搜索到局部最低点或鞍点时，即使梯度为0，但因为仍然具有速度，所以会冲破该点（听上去就像是给搜索点加了惯性和摩擦力）。

对这个方法，还有另一种方案：Nesterov Momentum。前者是在搜索点分别计算梯度和速度，然后计算其合方向；后者则是先计算速度，然后在使用这个速度到达的点处计算梯度，然后再朝着梯度的方向前进（按照直觉，后者的效率应该更高些）。

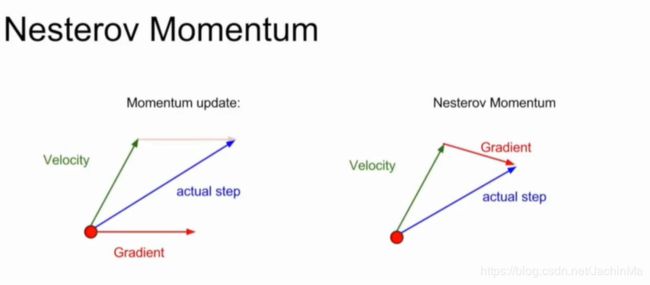
但是Nesterov Momentum的问题是，它将速度和梯度的计算分开，这会造成应用上的不便。为了解决这个问题，我们使用换元法：

另一个方法是AdaGrad：

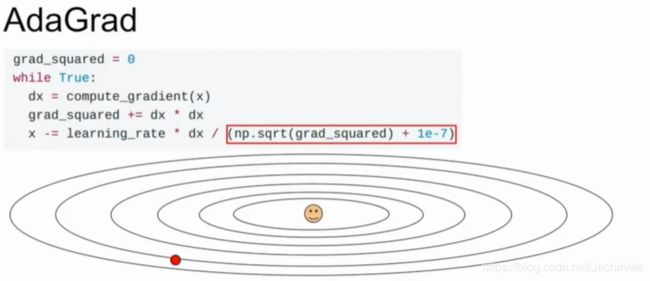
它的思路是在搜索方向时计算当前梯度的平方，并与之前的加和，并在移动步长上除以梯度的平方。这样做的好处是可以加速在小梯度方向的学习速度，而加速在大梯度方向的学习速度。但一定时间后，积累的梯度平方会导致步长越来越短。

(这里的1e-7也是一个超参数，它的目的是避免结果为0，但又尽量不对结果产生影响)

AdaGrad在计算凸函数时效果很好，但在计算非凸函数时，它很容易困在局部最小点。

为了改善这两个问题，我们提出了RMSProp：

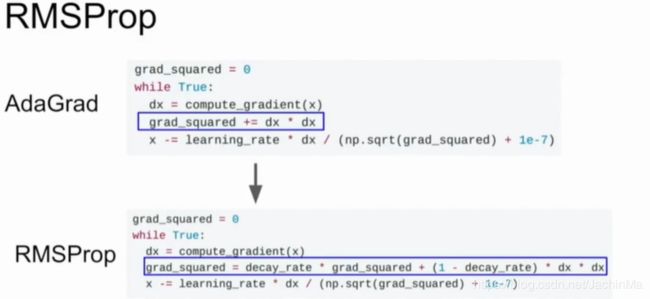
但RMSProp的问题是，由于梯度被缩减了，这可能导致训练速度下降。

上述的两类方法，一类给搜索点加了惯性以冲破鞍点和局部极小点，另一类除以梯度平方和以得到更好的搜索速度，看上去这两种思路并没有冲突，那为什么不把它们结合呢？

以下是一个思路：

但这种方法的问题是，由于第一和第二动量的初始值设为0，这可能导致初始步长变得过大而使后续的更新变得困难。为了改善这一问题，Adam方法进行了改进：

完整版的Adam算法加入了第一和第二动量的偏置项：其实为了 避免步长过大，只要在步长项乘以一个小数即可。但为了使算法灵活，能够满足各种数据和要求对算法的要求，这里设置了两个偏置项。实际上如果beta1和beta2和值相同时，Adam算法此时就等效于给步长乘以一个小数。

但Adam算法也不算尽善尽美：在处理梯度变化较大和较小的方向分别与坐标轴平行的数据时，它的效果非常好；但对于那些不是的数据，它的效果就不那么令人满意了。

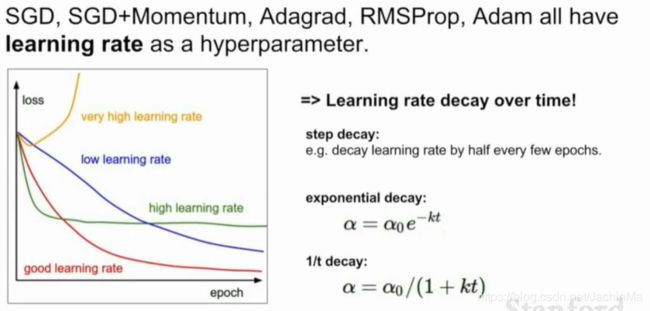
通常学习率在训练过程中是不变的，但如果我们让它变化呢？这有时候会是个好主意，但要注意，由于学习率的衰减指数是一个二阶超参数，所以通常最好在观察了不设置衰减的损失函数后，知道了自己需要在什么地方做出怎样的衰减后，再来考虑衰减的问题。

关于优化的另一个问题是：我们目前使用的方法都是一阶偏导。我们计算当前点的最大梯度，并朝着这个方向前进一步。但因为梯度只在很小的区间内有效，这就限制了步长的选择。为了改善这个问题，我们考虑一个新思路：

所谓的求梯度，其实就是求函数的一阶偏导。那如果我们求其二阶偏导呢？二阶偏导可以在一个比梯度更大的区间内模拟函数，且由于是二阶偏导，我们可以很容易地求得其最小值。这就是二阶优化，也被称为牛顿法。

但这种方法的问题是，由于海森矩阵要计算所有参数的偏导，对具有成百上千个参数的深度学习来说，这要耗费太多的算力。

为了解决这个问题，有很多改进的算法被提出：

比如BGFS：使用一阶更新来接近海森矩阵的逆。以及BGFS的改进算法：L-BGFS：它并不存储全部的海森矩阵逆(但没说具体做法)。

它在数据和参数较少及噪音不大的数据集上运行效果较好，但在其它的大多数情况下，最好还是使用Adam算法。

课程这里还介绍了模型集成的方法：使用多个样本训练多个分类器(有时超参数或其它设置也不同)，并取其平均值或投票结果作为最终结果。它对解决过拟合问题有着很好 的效果。

还有一个模型训练的小技巧：

Polyak的做法是在做模型训练时，对不同时刻的每个模型参数，求其指数衰减，之后使用这些平滑衰减平均后的模型参数作为参数。

正则化

正则化可以提高单模型的表现，其原理是在模型中加入一些东西，来防止过拟合，从而在测试集中得到更好的表现。

一种方法是在损失函数中加入一个数据项：

Dropsout的做法则是，在正向传播时随机将每一层中的一些神经元置零。对其有效性的一个解释是，它类似于模型集成思想，把每个神经元视作一个模型，然后随机选取数个模型集成。

但它的问题是，它在训练时引入了随机性。但这在测试时不是个好消息，我们不希望重复运行时，却得出了不同的分类结果。于是一个思路是，计算其期望来边缘化随机性。但这个期望是很难计算的。一个取巧的方法是，在测试时，对其结果乘以置零的神经元的比例p：

我们通常使用GPU来进行训练，所以多一个乘法运算并不是什么事。但在测试时，运行的设备是不确定的，因此我们希望能够尽可能地减少运算。解决这问题的一个方法是Inverted dropout：在测试时，并不使用全部权重矩阵，而是除以置零的概率p。

batch normolization也能起到类似的效果，但它因为没有p这样一个超参数来调节，所以在灵活性上不如dropout。

还有一些和dropout思想类似的方法：dropconnect：随机将一些输入置零；随机层：在训练时随机跳过一些层，但在测试时使用全部层。

正则化的另一个思路是数据增强：在训练时对数据进行处理：翻转、裁切、色彩抖动、旋转、拉伸、透镜畸变以及以上方法的组合，然后使用处理后的数据进行训练。

还有一种有趣的方法是随机池化。

迁移学习

迁移学习也是为了解决过拟合，同时它还解决了需要大型数据集才能训练CNN的问题。

它的思路是，首先构建一个CNN，将其在一个大的训练集上进行训练，然后对训练好的模型，根据你的数据的情况，来进行一定的微调：

迁移学习最大的好处是，避免了重复造轮子的辛苦，也降低了CNN的门槛：大量的数据集以及昂贵的GPU不再是CNN的必备品了，这对CNN的应用来说是件好事。