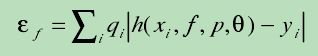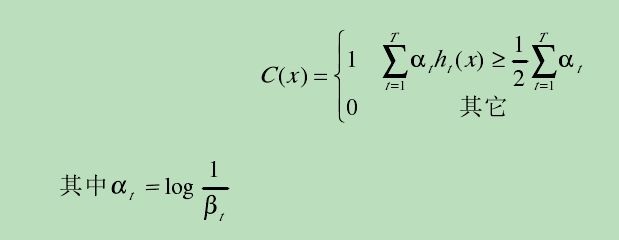浅析人脸检测之Haar分类器方法:Haar特征、积分图、 AdaBoost 、级联
转自:http://www.cnblogs.com/ello/archive/2012/04/28/2475419.html
由于工作需要,我开始研究人脸检测部分的算法,这期间断断续续地学习Haar分类器的训练以及检测过程,在这里根据各种论文、网络资源的查阅和对代码的理解做一个简单的总结。我试图概括性的给出算法的起源、全貌以及细节的来龙去脉,但是水平有限,只能解其大概,希望对初学者起到帮助,更主要的是对我个人学习的一次提炼。
一、Haar分类器的前世今生
人脸检测属于计算机视觉的范畴,早期人们的主要研究方向是人脸识别,即根据人脸来识别人物的身份,后来在复杂背景下的人脸检测需求越来越大,人脸检测也逐渐作为一个单独的研究方向发展起来。
目前的人脸检测方法主要有两大类:基于知识和基于统计。
“基于知识的方法主要利用先验知识将人脸看作器官特征的组合,根据眼睛、眉毛、嘴巴、鼻子等器官的特征以及相互之间的几何位置关系来检测人脸。基于统计的方法则将人脸看作一个整体的模式——二维像素矩阵,从统计的观点通过大量人脸图像样本构造人脸模式空间,根据相似度量来判断人脸是否存在。在这两种框架之下,发展了许多方法。目前随着各种方法的不断提出和应用条件的变化,将知识模型与统计模型相结合的综合系统将成为未来的研究趋势。”(来自论文《基于Adaboost的人脸检测方法及眼睛定位算法研究》)
基于知识的人脸检测方法
Ø 模板匹配
Ø 人脸特征
Ø 形状与边缘
Ø 纹理特性
Ø 颜色特征
基于统计的人脸检测方法
Ø 主成分分析与特征脸
Ø 神经网络方法
Ø 支持向量机
Ø 隐马尔可夫模型
Ø Adaboost算法
本文中介绍的Haar分类器方法,包含了Adaboost算法,稍候会对这一算法做详细介绍。所谓分类器,在这里就是指对人脸和非人脸进行分类的算法,在机器学习领域,很多算法都是对事物进行分类、聚类的过程。OpenCV中的ml模块提供了很多分类、聚类的算法。
注:聚类和分类的区别是什么?一般对已知物体类别总数的识别方式我们称之为分类,并且训练的数据是有标签的,比如已经明确指定了是人脸还是非人脸,这是一种有监督学习。也存在可以处理类别总数不确定的方法或者训练的数据是没有标签的,这就是聚类,不需要学习阶段中关于物体类别的信息,是一种无监督学习。
其中包括Mahalanobis距离、K均值、朴素贝叶斯分类器、决策树、Boosting、随机森林、Haar分类器、期望最大化、K近邻、神经网络、支持向量机。
我们要探讨的Haar分类器实际上是Boosting算法的一个应用,Haar分类器用到了Boosting算法中的AdaBoost算法,只是把AdaBoost算法训练出的强分类器进行了级联,并且在底层的特征提取中采用了高效率的矩形特征和积分图方法,这里涉及到的几个名词接下来会具体讨论。
虽说haar分类器采用了Boosting的算法,但在OpenCV中,Haar分类器与Boosting没有采用同一套底层数据结构,《Learning OpenCV》中有这样的解释:“Haar分类器,它建立了boost筛选式级联分类器。它与ML库中其他部分相比,有不同的格局,因为它是在早期开发的,并完全可用于人脸检测。”
是的,在2001年,Viola和Jones两位大牛发表了经典的《Rapid Object Detection using a Boosted Cascade of Simple Features》【1】和《Robust Real-Time Face Detection》【2】,在AdaBoost算法的基础上,使用Haar-like小波特征和积分图方法进行人脸检测,他俩不是最早使用提出小波特征的,但是他们设计了针对人脸检测更有效的特征,并对AdaBoost训练出的强分类器进行级联。这可以说是人脸检测史上里程碑式的一笔了,也因此当时提出的这个算法被称为Viola-Jones检测器。又过了一段时间,Rainer Lienhart和Jochen Maydt两位大牛将这个检测器进行了扩展【3】,最终形成了OpenCV现在的Haar分类器。之前我有个误区,以为AdaBoost算法就是Viola和Jones搞出来的,因为网上讲Haar分类器的地方都在大讲特讲AdaBoost,所以我错觉了,后来理清脉络,AdaBoost是Freund 和Schapire在1995年提出的算法,是对传统Boosting算法的一大提升。Boosting算法的核心思想,是将弱学习方法提升成强学习算法,也就是“三个臭皮匠顶一个诸葛亮”,它的理论基础来自于Kearns 和Valiant牛的相关证明【4】,在此不深究了。反正我是能多简略就多简略的把Haar分类器的前世今生说完鸟,得出的结论是,大牛们都是成对儿的。。。额,回到正题,Haar分类器 = Haar-like特征 + 积分图方法 + AdaBoost + 级联;
注:为何称其为Haar-like?这个名字是我从网上看来的,《Learning OpenCV》中文版提到Haar分类器使用到Haar特征,但这种说法不确切,应该称为类Haar特征,Haar-like就是类Haar特征的意思。
二、Haar分类器的浅入浅出
之所以是浅入浅出是因为,我暂时深入不能,只是根据其他人的总结,我加以梳理归纳,用自己的理解阐述出来,难免会有错误,欢迎指正。
Haar分类器算法的要点如下:
① 使用Haar-like特征做检测。
② 使用积分图(Integral Image)对Haar-like特征求值进行加速。
③ 使用AdaBoost算法训练区分人脸和非人脸的强分类器。
④ 使用筛选式级联把强分类器级联到一起,提高准确率。
2.1 Haar-like特征你是何方神圣?
一看到Haar-like特征这玩意儿就头大的人举手。好,很多人。那么我先说下什么是特征,我把它放在下面的情景中来描述,假设在人脸检测时我们需要有这么一个子窗口在待检测的图片窗口中不断的移位滑动,子窗口每到一个位置,就会计算出该区域的特征,然后用我们训练好的级联分类器对该特征进行筛选,一旦该特征通过了所有强分类器的筛选,则判定该区域为人脸。
那么这个特征如何表示呢?好了,这就是大牛们干的好事了。后人称这他们搞出来的这些东西叫Haar-Like特征。
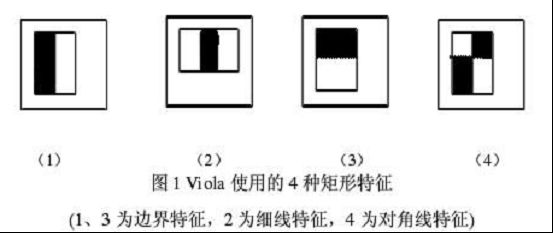
下面是Viola牛们提出的Haar-like特征。
下面是Lienhart等牛们提出的Haar-like特征。
这些所谓的特征不就是一堆堆带条纹的矩形么,到底是干什么用的?我这样给出解释,将上面的任意一个矩形放到人脸区域上,然后,将白色区域的像素和减去黑色区域的像素和,得到的值我们暂且称之为人脸特征值,如果你把这个矩形放到一个非人脸区域,那么计算出的特征值应该和人脸特征值是不一样的,而且越不一样越好,所以这些方块的目的就是把人脸特征量化,以区分人脸和非人脸。
为了增加区分度,可以对多个矩形特征计算得到一个区分度更大的特征值,那么什么样的矩形特征怎么样的组合到一块可以更好的区分出人脸和非人脸呢,这就是AdaBoost算法要做的事了。这里我们先放下积分图这个概念不管,为了让我们的思路连贯,我直接开始介绍AdaBoost算法。
2.2 AdaBoost你给我如实道来!
本节旨在介绍AdaBoost在Haar分类器中的应用,所以只是描述了它在Haar分类器中的特性,而实际上AdaBoost是一种具有一般性的分类器提升算法,它使用的分类器并不局限某一特定算法。
上面说到利用AdaBoost算法可以帮助我们选择更好的矩阵特征组合,其实这里提到的矩阵特征组合就是我们之前提到的分类器,分类器将矩阵组合以二叉决策树的形式存储起来。
我现在脑子里浮现了很多问题,总结起来大概有这么些个:
v 弱分类器和强分类器是什么?
v 弱分类器是怎么得到的?
v 强分类器是怎么得到的?
v 二叉决策树是什么?
要回答这一系列问题,我得跟你罗嗦一会儿了,这得从AdaBoost的身世说起。
2.2.1 AdaBoost的身世之谜
关于AdaBoost的身世,我把相关英文文献从上世纪80年代一直下到2001年,我发现我在短时间内没法读完,所以我只能尝试着从别人的总结中拼凑那些离散的片段,难免有误。
之前讲Haar分类器的前世今生也简单说过AdaBoost的身世,但是说的还不透。我比较喜欢查算法的户口,所以新写了一章查了下去。
AdaBoost的老祖宗可以说是机器学习的一个模型,它的名字叫PAC(Probably Approximately Correct)。
PAC模型是计算学习理论中常用的模型,是Valiant牛在我还没出生的1984年提出来的【5】,他认为“学习"是模式明显清晰或模式不存在时仍能获取知识的一种“过程”,并给出了一个从计算角度来获得这种“过程"的方法,这种方法包括:
(1)适当信息收集机制的选择;
(2)学习的协定;
(3)对能在合理步骤内完成学习的概念的分类。
PAC学习的实质就是在样本训练的基础上,使算法的输出以概率接近未知的目标概念。PAC学习模型是考虑样本复杂度(指学习器收敛到成功假设时至少所需的训练样本数)和计算复杂度(指学习器收敛到成功假设时所需的计算量)的一个基本框架,成功的学习被定义为形式化的概率理论。(来自论文《基于Adaboost的人脸检测方法及眼睛定位算法研究》)
简单说来,PAC学习模型不要求你每次都正确,只要能在多项式个样本和多项式时间内得到满足需求的正确率,就算是一个成功的学习。
基于PAC学习模型的理论分析,Valiant牛提出了Boosting算法【5】,Boosting算法涉及到两个重要的概念就是弱学习和强学习,所谓的弱学习,就是指一个学习算法对一组概念的识别率只比随机识别好一点,所谓强学习,就是指一个学习算法对一组概率的识别率很高。现在我们知道所谓的弱分类器和强分类器就是弱学习算法和强学习算法。弱学习算法是比较容易获得的,获得过程需要数量巨大的假设集合,这个假设集合是基于某些简单规则的组合和对样本集的性能评估而生成的,而强学习算法是不容易获得的,然而,Kearns 和Valiant 两头牛提出了弱学习和强学习等价的问题 【6】 并证明了只要有足够的数据,弱学习算法就能通过集成的方式生成任意高精度的强学习方法。这一证明使得Boosting有了可靠的理论基础,Boosting算法成为了一个提升分类器精确性的一般性方法。【4】
1990年,Schapire牛提出了第一个多项式时间的算法【7】,1年后Freund牛又提出了一个效率更高的Boosting算法【8】。然而,Boosting算法还是存在着几个主要的问题,其一Boosting算法需要预先知道弱学习算法学习正确率的下限即弱分类器的误差,其二Boosting算法可能导致后来的训练过分集中于少数特别难区分的样本,导致不稳定。针对Boosting的若干缺陷,Freund和Schapire牛于1996年前后提出了一个实际可用的自适应Boosting算法AdaBoost【9】,AdaBoost目前已发展出了大概四种形式的算法,Discrete AdaBoost(AdaBoost.M1)、Real AdaBoost、LogitBoost、gentle AdaBoost,本文不做一一介绍。至此,AdaBoost的身世之谜就这样揭开鸟。同时弱分类器和强分类器是什么的问题也解释清楚了。剩下3个问题,我们先看一下,弱分类器是如何得到的。
2.2.2 弱分类器的孵化
最初的弱分类器可能只是一个最基本的Haar-like特征,计算输入图像的Haar-like特征值,和最初的弱分类器的特征值比较,以此来判断输入图像是不是人脸,然而这个弱分类器太简陋了,可能并不比随机判断的效果好,对弱分类器的孵化就是训练弱分类器成为最优弱分类器,注意这里的最优不是指强分类器,只是一个误差相对稍低的弱分类器,训练弱分类器实际上是为分类器进行设置的过程。至于如何设置分类器,设置什么,我们首先分别看下弱分类器的数学结构和代码结构。
² 数学结构
一个弱分类器![]() 由子窗口图像x,一个特征f,指示不等号方向的p和阈值
由子窗口图像x,一个特征f,指示不等号方向的p和阈值![]() 组成。P的作用是控制不等式的方向,使得不等式都是<号,形式方便。
组成。P的作用是控制不等式的方向,使得不等式都是<号,形式方便。
² 代码结构
2 * CART classifier
3 */
4 typedef struct CvCARTHaarClassifier
5 {
6 CV_INT_HAAR_CLASSIFIER_FIELDS()
7 int count;
8 int* compidx;
9 CvTHaarFeature* feature;
10 CvFastHaarFeature* fastfeature;
11 float* threshold;
12 int* left;
13 int* right;
14 float* val;
15 } CvCARTHaarClassifier;
代码结构中的threshold即代表数学结构中的![]() 阈值。
阈值。
这个阈值究竟是干什么的?我们先了解下CvCARTHaarClassifier这个结构,注意CART这个词,它是一种二叉决策树,它的提出者Leo Breiman等牛称其为“分类和回归树(CART)”。什么是决策树?我如果细讲起来又得另起一章,我只简略介绍它。
“机器学习中,决策树是一个预测模型;他代表的是对象属性与对象值之间的一种映射关系。树中每个节点表示某个对象,而每个分叉路径则代表的某个可能的属性值,而每个叶结点则对应从根节点到该叶节点所经历的路径所表示的对象的值。决策树仅有单一输出,若欲有复数输出,可以建立独立的决策树以处理不同输出。从数据产生决策树的机器学习技术叫做决策树学习, 通俗说就是决策树。”(来自《维基百科》)
决策树包含:分类树,回归树,分类和回归树(CART),CHAID 。
分类和回归的区别是,分类是当预计结果可能为两种类型(例如男女,输赢等)使用的概念。 回归是当局域结果可能为实数(例如房价,患者住院时间等)使用的概念。
决策树用途很广可以分析因素对事件结果的影响(详见维基百科),同时也是很常用的分类方法,我举个最简单的决策树例子,假设我们使用三个Haar-like特征f1,f2,f3来判断输入数据是否为人脸,可以建立如下决策树:
可以看出,在分类的应用中,每个非叶子节点都表示一种判断,每个路径代表一种判断的输出,每个叶子节点代表一种类别,并作为最终判断的结果。
一个弱分类器就是一个基本和上图类似的决策树,最基本的弱分类器只包含一个Haar-like特征,也就是它的决策树只有一层,被称为树桩(stump)。
最重要的就是如何决定每个结点判断的输出,要比较输入图片的特征值和弱分类器中特征,一定需要一个阈值,当输入图片的特征值大于该阈值时才判定其为人脸。训练最优弱分类器的过程实际上就是在寻找合适的分类器阈值,使该分类器对所有样本的判读误差最低。
具体操作过程如下:
1)对于每个特征 f,计算所有训练样本的特征值,并将其排序。
扫描一遍排好序的特征值,对排好序的表中的每个元素,计算下面四个值:
全部人脸样本的权重的和t1;
全部非人脸样本的权重的和t0;
在此元素之前的人脸样本的权重的和s1;
在此元素之前的非人脸样本的权重的和s0;
2)最终求得每个元素的分类误差![]()
在表中寻找r值最小的元素,则该元素作为最优阈值。有了该阈值,我们的第一个最优弱分类器就诞生了。
在这漫长的煎熬中,我们见证了一个弱分类器孵化成长的过程,并回答了如何得到弱分类器以及二叉决策树是什么。最后的问题是强分类器是如何得到的。
2.2.3 弱分类器的化蝶飞
首先看一下强分类器的代码结构:
2 typedef struct CvStageHaarClassifier
3 {
4 CV_INT_HAAR_CLASSIFIER_FIELDS()
5 int count;
6 float threshold;
7 CvIntHaarClassifier** classifier;
8 }CvStageHaarClassifier;
typedef struct CvIntHaarClassifier
{
CV_INT_HAAR_CLASSIFIER_FIELDS()
} CvIntHaarClassifier;
强分类器的诞生需要T轮的迭代,具体操作如下:
1. 给定训练样本集S,共N个样本,其中X和Y分别对应于正样本和负样本; T为训练的最大循环次数;
2. 初始化样本权重为1/N ,即为训练样本的初始概率分布;
3. 第一次迭代训练N个样本,得到第一个最优弱分类器,步骤见2.2.2节
4. 提高上一轮中被误判的样本的权重;
5. 将新的样本和上次本分错的样本放在一起进行新一轮的训练。
6. 循环执行4-5步骤,T轮后得到T个最优弱分类器。
7.组合T个最优弱分类器得到强分类器,组合方式如下:
===========================来自他处的步骤分析方便理解========================
1. 归一化权重:
2、对于每一个特征f,训练一个弱分类器h;计算所以特征的加权错误率εf,
3、选取具有最小错误率εf的弱分类器hi
4、调整权重
——级联成最终强分类器
====================================================
相当于让所有弱分类器投票,再对投票结果按照弱分类器的错误率加权求和,将投票加权求和的结果与平均投票结果比较得出最终的结果。
至此,我们看到其实我的题目起的漂亮却并不贴切,强分类器的脱颖而出更像是民主的投票制度,众人拾材火焰高,强分类器不是个人英雄主义的的产物,而是团结的力量。但从宏观的局外的角度看,整个AdaBoost算法就是一个弱分类器从孵化到化蝶的过程。小人物的奋斗永远是理想主义者们津津乐道的话题。但暂时让我们放下AdaBoost继续探讨Haar分类器的其他特性吧。
2.3 强分类器的强强联手
至今为止我们好像一直在讲分类器的训练,实际上Haar分类器是有两个体系的,训练的体系,和检测的体系。训练的部分大致都提到了,还剩下最后一部分就是对筛选式级联分类器的训练。我们看到了通过AdaBoost算法辛苦的训练出了强分类器,然而在现实的人脸检测中,只靠一个强分类器还是难以保证检测的正确率,这个时候,需要一个豪华的阵容,训练出多个强分类器将它们强强联手,最终形成正确率很高的级联分类器这就是我们最终的目标Haar分类器。
那么训练级联分类器的目的就是为了检测的时候,更加准确,这涉及到Haar分类器的另一个体系,检测体系,检测体系是以现实中的一幅大图片作为输入,然后对图片中进行多区域,多尺度的检测,所谓多区域,是要对图片划分多块,对每个块进行检测,由于训练的时候用的照片一般都是20*20左右的小图片,所以对于大的人脸,还需要进行多尺度的检测,多尺度检测机制一般有两种策略,一种是不改变搜索窗口的大小,而不断缩放图片,这种方法显然需要对每个缩放后的图片进行区域特征值的运算,效率不高,而另一种方法,是不断初始化搜索窗口size为训练时的图片大小,不断扩大搜索窗口,进行搜索,解决了第一种方法的弱势。在区域放大的过程中会出现同一个人脸被多次检测,这需要进行区域的合并,这里不作探讨。
无论哪一种搜索方法,都会为输入图片输出大量的子窗口图像,这些子窗口图像经过筛选式级联分类器会不断地被每一个节点筛选,抛弃或通过。
它的结构如图所示。
我想你一定觉得很熟悉,这个结构不是很像一个简单的决策树么。
在代码中,它的结构如下:
2 typedef struct CvTreeCascadeNode
3 {
4 CvStageHaarClassifier* stage;
5 struct CvTreeCascadeNode* next;
6 struct CvTreeCascadeNode* child;
7 struct CvTreeCascadeNode* parent;
8 struct CvTreeCascadeNode* next_same_level;
9 struct CvTreeCascadeNode* child_eval;
10 int idx;
11 int leaf;
12 } CvTreeCascadeNode;
13 /* internal tree cascade classifier */
14 typedef struct CvTreeCascadeClassifier
15 {
16 CV_INT_HAAR_CLASSIFIER_FIELDS()
17 CvTreeCascadeNode* root; /* root of the tree */
18 CvTreeCascadeNode* root_eval; /* root node for the filtering */
19 int next_idx;
20 } CvTreeCascadeClassifier;
级联强分类器的策略是,将若干个强分类器由简单到复杂排列,希望经过训练使每个强分类器都有较高检测率,而误识率可以放低,比如几乎99%的人脸可以通过,但50%的非人脸也可以通过,这样如果有20个强分类器级联,那么他们的总识别率为0.99^20 ![]() 98%,错误接受率也仅为0.5^20
98%,错误接受率也仅为0.5^20 ![]() 0.0001%。这样的效果就可以满足现实的需要了,但是如何使每个强分类器都具有较高检测率呢,为什么单个的强分类器不可以同时具有较高检测率和较高误识率呢?
0.0001%。这样的效果就可以满足现实的需要了,但是如何使每个强分类器都具有较高检测率呢,为什么单个的强分类器不可以同时具有较高检测率和较高误识率呢?
下面我们讲讲级联分类器的训练。(主要参考了论文《基于Adaboost的人脸检测方法及眼睛定位算法研究》)
设K是一个级联检测器的层数,D是该级联分类器的检测率,F是该级联分类器的误识率,di是第i层强分类器的检测率,fi是第i层强分类器的误识率。如果要训练一个级联分类器达到给定的F值和D值,只需要训练出每层的d值和f值,这样:
d^K = D,f^K = F
级联分类器的要点就是如何训练每层强分类器的d值和f值达到指定要求。
AdaBoost训练出来的强分类器一般具有较小的误识率,但检测率并不很高,一般情况下,高检测率会导致高误识率,这是强分类阈值的划分导致的,要提高强分类器的检测率既要降低阈值,要降低强分类器的误识率就要提高阈值,这是个矛盾的事情。据参考论文的实验结果,增加分类器个数可以在提高强分类器检测率的同时降低误识率,所以级联分类器在训练时要考虑如下平衡,一是弱分类器的个数和计算时间的平衡,二是强分类器检测率和误识率之间的平衡。具体训练方法如下,我用伪码的形式给出:
1)设定每层最小要达到的检测率d,最大误识率f,最终级联分类器的误识率Ft;
2)P=人脸训练样本,N=非人脸训练样本,D0=1.0,F0=1.0;
3)i=0;
4)for : Fi>Ft
l ++i;
l ni=0;Fi=Fi-1;
l for : Fi>f*Fi-1
n ++ni;
n 利用AdaBoost算法在P和N上训练具有ni个弱分类器的强分类器;
n 衡量当前级联分类器的检测率Di和误识率Fi;
n for : di
Ø 降低第i层的强分类器阈值;
Ø 衡量当前级联分类器的检测率Di和误识率Fi;
n N = Φ;
n 利用当前的级联分类器检测非人脸图像,将误识的图像放入N;
2.4 积分图是一个加速器
之所以放到最后讲积分图(Integral image),不是因为它不重要,正相反,它是Haar分类器能够实时检测人脸的保证。当我把Haar分类器的主脉络都介绍完后,其实在这里引出积分图的概念恰到好处。
在前面的章节中,我们熟悉了Haar-like分类器的训练和检测过程,你会看到无论是训练还是检测,每遇到一个图片样本,每遇到一个子窗口图像,我们都面临着如何计算当前子图像特征值的问题,一个Haar-like特征在一个窗口中怎样排列能够更好的体现人脸的特征,这是未知的,所以才要训练,而训练之前我们只能通过排列组合穷举所有这样的特征,仅以Viola牛提出的最基本四个特征为例,在一个24×24size的窗口中任意排列至少可以产生数以10万计的特征,对这些特征求值的计算量是非常大的。
而积分图就是只遍历一次图像就可以求出图像中所有区域像素和的快速算法,大大的提高了图像特征值计算的效率。
我们来看看它是怎么做到的。
积分图是一种能够描述全局信息的矩阵表示方法。积分图的构造方式是位置(i,j)处的值ii(i,j)是原图像(i,j)左上角方向所有像素的和:
积分图构建算法:
1)用s(i,j)表示行方向的累加和,初始化s(i,-1)=0;
2)用ii(i,j)表示一个积分图像,初始化ii(-1,i)=0;
3)逐行扫描图像,递归计算每个像素(i,j)行方向的累加和s(i,j)和积分图像ii(i,j)的值
s(i,j)=s(i,j-1)+f(i,j)
ii(i,j)=ii(i-1,j)+s(i,j)
4)扫描图像一遍,当到达图像右下角像素时,积分图像ii就构造好了。
积分图构造好之后,图像中任何矩阵区域的像素累加和都可以通过简单运算得到如图所示。
设D的四个顶点分别为α、β、γ、δ,则D的像素和可以表示为
Dsum = ii( α )+ii( β)-(ii( γ)+ii( δ ));
而Haar-like特征值无非就是两个矩阵像素和的差,同样可以在常数时间内完成。
三、Haar分类器你敢更快点吗?!
这一章我简略的探讨下Haar分类器的检测效率。
我尝试过的几种方法:
1)尝试检测算法与跟踪算法相结合,原本以为Camshift是个轻量级的算法,但是正如我后来看到的,建立反向投影图的效率实在不高,在PC上效果不错,但是在ios上速度很慢,这个我后来发现可能是因为ios浮点运算效率不高的原因。但是即便速度能上去,靠Camshift跟踪算法太依赖肤色了,导致脖子,或是手什么的干扰很严重,这个调起来很费神,也不一定能调好。
2)修改OpenCV中Haar检测函数的参数,效果非常明显,得出的结论是,搜索窗口的搜索区域是提高效率的关键。
3)根据2)的启发,我打算利用YCbCr颜色空间,粗估肤色区域,以减少人脸的搜索面积,但是后来苦于没能高效率的区分出肤色区域,放弃了该方法。
4)换了策略,考虑到视频中人脸检测的特殊性,上一帧人脸的位置信息对下一帧的检测有很高的指导价值,所以采有帧间约束的方法,减少了人脸搜索的区域,并且动态调整Haar检测函数的参数,得到了较高的效率。
5)其他关于算法之外的优化需要根据不同的处理器做具体的优化。
四、总结
之前没怎么接触到计算机视觉领域,这次reseach对我来说是一个不小的挑战,发现其中涉及大量的数学知识,线代,统计学,数学分析等等,虽然感到困难重重,但我感到莫大的兴趣,尤其是机器学习领域,在我眼前展开的是一幅美妙的画面,大牛们神乎其技各显神通,复杂的数学公式背后蕴含着简单的哲理和思想。
人类的发展来源于对自然背后神秘力量的好奇和膜拜,简单的结构往往构建出让人难以想象的伟大,0和1构成了庞大的电子信息世界,DNA构成了自己都无法完全了解自己的生命体,夸克或是比夸克还小的粒子构成了这个令人着迷的宇宙,在这些简单的结构背后,是什么在注视着我们,狭义的编程只是在计算机的硬件躯壳内构建可执行的程序,而广义的编程在我看来是创造世界的一种手段。
现在,我给你一个创造世界的机会,你是用Vim还是Emacs,也许你会调侃的跟我说:
“恩,我用E = mc^2”。
附录:
论文列表:【1】《Rapid Object Detection using a Boosted Cascade of Simple Features》
【2】《Robust Real-Time Face Detection》
【3】《 An Extended Set of Haar-like Features for Rapid Object Detection》【4】《Crytographic Limitations on Learning Boolean Formulae and Finite Automata》
【5】《A Theory of the Learnable》
【6】《The Computational Complexity of Machine Learning》
【7】《The Strength of Weak Learnability》
【8】《Boosting a weak learning algorithm》
【9】《A Decision-Theoretic Generalization of On-Line Learning and an Application to Boosting》