动手实现Logistic Regression
算法思想
Logistic Regression是一种分类算法,一般处理的是二分类的问题,标签为离散值(如{0,1}),通过给定的训练样本集合(训练数据和标签),训练出最佳的回归系数,也称为权重矩阵,然后利用该权重矩阵对新样本进行预测,并给出最终的对应分类。
预测时,首先计算
其中x为训练样本,x=(x1,x2,…,xn),w为权重矩阵,w=(w0,w1,…,wn),x0一般设为1,x0w0称为偏置项
(说明:很多地方也有这样的写法:![]() ,其中b为偏置项,这里的b和w0x0是一个作用,所以我这里为了整齐划一,也为了方便理解,就不引入b这一项)
,其中b为偏置项,这里的b和w0x0是一个作用,所以我这里为了整齐划一,也为了方便理解,就不引入b这一项)
然后将z作为输入送到一个被称作“阈值函数”中,不同于感知器的是,逻辑回归的的阈值函数是一个连续函数,一般为Sigmoid函数:![]() ,函数图像为:
,函数图像为:

当sigmoid(z)>0.5时,判定预测样本属于1这一类,当sigmoid(z)<0.5时,判定预测样本属于0这一类,分界点为sigmoid(z)=0.5,即w.Tx=0,此时w.Tx=0即为分类的决策面。
训练权重矩阵

我们可以看到,上述预测步骤包括数据,阈值函数都是已知的,唯独权重矩阵W是未知的,那么接下来的工作就是要训练出符合期望的权重矩阵。
要想W达到最优,就是要让最终的预测结果尽量准确,即错误尽量最小,也称损失尽量最小,对于逻辑回归来说,其属于类别y的概率为:
![]()
那么对于m个训练样本

其似然函数为:

对于似然函数求解我们并不陌生,直接两边取对数,而在逻辑回归中,通常将负的对数似然函数作为其损失函数,即:
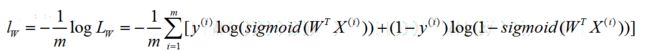
我们寻找最优权重W的问题转化为求解![]()
这里由于y是一个离散值,所以上述公式我们并不能求出一个公式解,只能使用梯度下降法来不断优化损失函数,并最终找到一个使得损失函数达到最小值的最优解,即我们要求的权重W,其中α为步长:
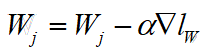
那么我们话不多说,直接动手推导损失函数的梯度:
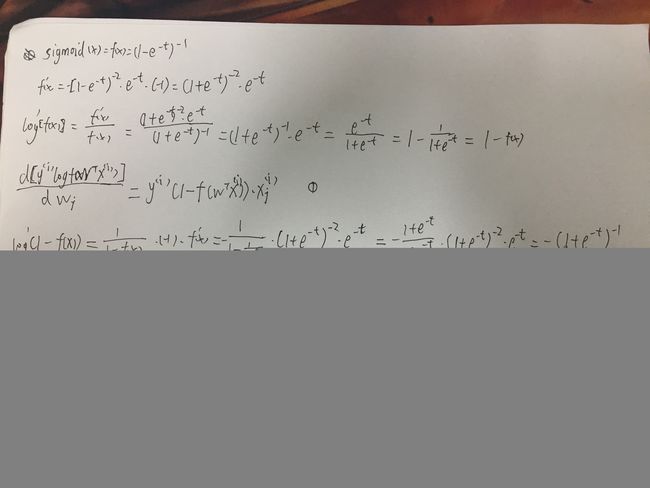
最终得到损失函数的梯度:
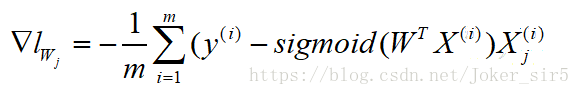
转换到矩阵计算,一般地:

这样我们就可以在一定的迭代次数内,不断地优化权重,使其达到最优(损失函数达到极小值)
关键代码
1.导入数据
仍然使用iris数据集,并且为了方便可视化,只取前两个特征进行训练,逻辑回归只处理二分类问题,所以只取0,1两类
并将数据分割为train set和test set
iris = datasets.load_iris()
X = iris.data
y = iris.target
X = X[y < 2, :2]
y = y[y < 2]
X_train, y_train, X_test, y_test = data_split(X, y, seed=666)
2.计算sigmoid值
def sigmoid(x): # sigmoid函数
return 1.0 / (1 + np.exp(-x))
3.计算梯度
def error_rate(weight, X, y):
#X(nx3), weight(3x1),y(nx1)
return X.T.dot(sigmoid(X.dot(weight)) - y) / len(y)
4.利用梯度下降法优化W
def gradAscent(data, y): # 梯度下降求最优参数
alpha = 0.01 # 步长
maxCycles = 1000 # 设置迭代的次数
X = np.hstack([np.ones((len(data), 1)), data]) #构建系数矩阵,X(nx3)第一列默认置1,后两列为data原数据
weights = np.ones(X.shape[1]) # 设置初始的参数,并都赋默认值为1。注意这里权重以矩阵形式表示三个参数。3x1
for k in range(maxCycles):
error = error_rate(weights, X, y)
weights = weights - alpha * error # 迭代更新权重
return weights
hstack是numpy封装的一个水平方向拼接函数,对应vstack(垂直方向),非常方便,使用时注意拼接的方向,以及对应方向的维度要一致,这里就是将一个全为1的(mx1)矩阵和data(mx2)拼接成我们需要的系数矩阵(mx3),感兴趣的读者可以通过文档查看其用法
5.画出决策面
决策面方程为:
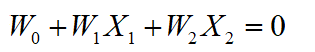
将特征X1放在x轴,特征X2放在y轴,即:

X, y = load_data()
plt.scatter(X[y == 0, 0], X[y == 0, 1], color="red")
plt.scatter(X[y == 1, 0], X[y == 1, 1], color="blue")
x1 = np.linspace(4, 8, 1000)
plt.plot(x1, (-weights[0]-weights[1]*x1)/weights[2])
plt.show()
结果如图:
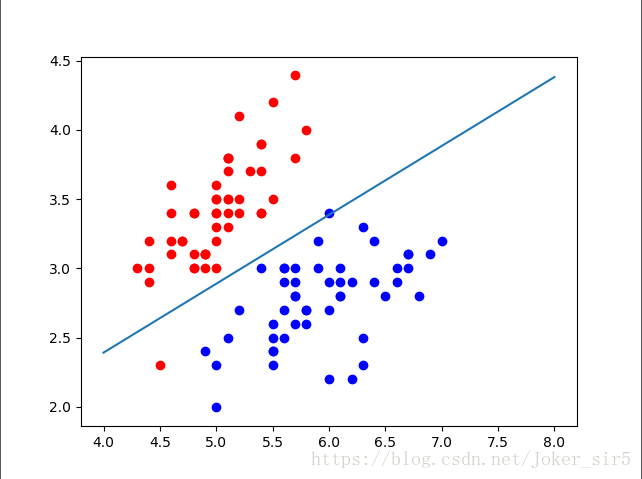
5.利用训练好的权重在test set上进行预测,并求出准确率:
# 预测
X = np.hstack([np.ones((len(predict_data), 1)), predict_data])
pro_y = sigmoid(X.dot(weights))
return np.array(pro_y >= 0.5, dtype='int')
np.sum(y == y_predict) / len(y)
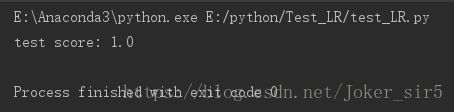
到此我们就动手完成了逻辑回归的权重训练,在test set上的准确率达到1,符合期望效果,再有新的iris数据我们便可以使用我们训练的权重矩阵进行预测了
总结
1.对于为何使用sigmoid函数作为阈值函数,原因主要有三点:
1)相较于感知器的越阶函数,sigmoid函数是个连续函数,能够提供一个平缓的分类边界
2)sigmoid函数求解最优的过程使用了梯度信息和迭代公式,保证了收敛的素的及最优值的存在
3)损失函数是一个指数和对数的函数,是凸函数,所以算法的局部最优解就意味着也是全局最优
2.本篇博客利用梯度下降法求解最优,当然还有其他优化方法,如随机梯度下降,感兴趣的读者可以自行去实现,其中的参数包括步长、迭代次数也是直接给出的,在实际应用中,当准确率并未达到预期效果时,可能去要去进一步的调参,请参见。
3.逻辑回归中涉及了几处求和公式和矩阵运算的转换,在刚开始学习的时候,好不容易公式推明白了,但一到写代码的时候就手足无措了,比如这里,如何从
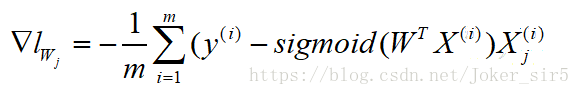
到

再到
X.T.dot(sigmoid(X.dot(weight)) - y) / len(y)
最后也是费了好大劲才转换过来这个思路,表明了线性代数这一块还有些许相对薄弱,在今后还需要多多练习!
注意:每次做矩阵运算的时候一定要搞清楚每个式子的维度,例如A.dot(B)和B.dot(A)在一般情况下是不相等的,包括做减法,一定要搞清楚A,B对应的是多少乘多少的矩阵(不妨像我一样在代码的注释里写出来),还有一点就是在numpy中,A(20x1)+B(1x20)是可以计算的(读者可以去试一试,因为我就是掉进这个坑里了。。。),最终会得到一个(20x20)的矩阵,那如果我们的想法是拿A+B得到一个(20x1)的矩阵,却没有注意A和B的维数,最终得到的结果可想而知,根本不是我们要的结果!
4.细心的读者从最终的分类决策面中可能发现,下方有个点是属于误分类的,但最终test set的准确率却为1,这是因为,在分割train set 和 test set时,该点是被分到train set中去了,所以在test set 中才会出现准确率=1的结果。
有任何问题欢迎留言交流!