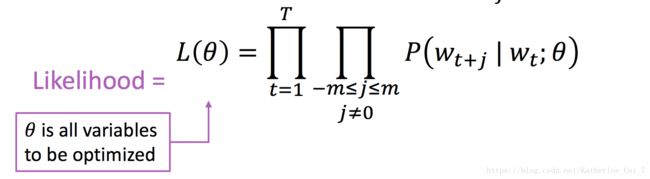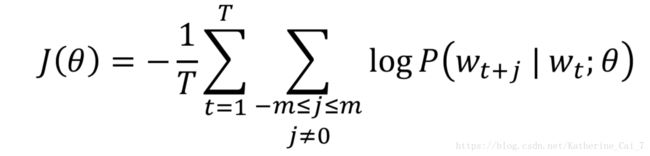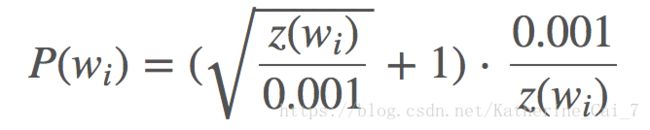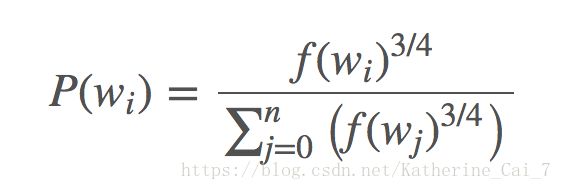word2vec详解
在NLP领域里,将一个单词用一个有限维的向量表示基本上已经成为现在进行文本处理的一个标配步骤。在word2vec这个神器出现以前,比较通用的解决步骤是WordNet,可以认为它是一个类似词典一样的存在,查每个词对应的同义词、上位词等信息,好虽好,但是需要人工维护,而且缺乏对词语新的含义的挖掘,不能做到实时更新,虽然能够找到一个词的同义词,但是词之间的相似度到底有多高这个指标很难度量。传统one-hot表示法是借用一个固定长度的词汇表,每个词代表其中的一维,词i出现时,词汇表中词i的位置标记为1,其余均为0。很显然,这种表示方法太过稀疏,而且无法度量词语之间的相似性(因为点乘之后结果都为0,均不相关)。为了解决上述问题,有了word2vec这么个东西出现。
统计NLP中有一个非常成功的观点:一个词的含义是由其上下文经常出现的词赋予的(A word's meaning is given by the words that frequently appear close-by)。所谓一个单词的上下文是指在其窗口中出现的词(一般情况窗口的size选5左右,即这个中心词的前5个词和后5个词,上下文词一共是10个词)。这里我们用c表示中心词,o表示中心词c的上下文词。要对每个词进行向量化的表示,间接转化为计算在给定中心词c的条件下,通过调整词向量来使上下文词o出现的概率最大化。根据上述描述,可以用如下数学函数对目标函数进行表示:
对上述函数最大化,等价于对其负对数似然函数求最小值,转化成如下目标函数
问题是如何求这个P(wt+j | wt; θ)。
这里我们对每个词w引入两个向量:当w为中心词时的向量![]() 和当w为上下文词时的向量
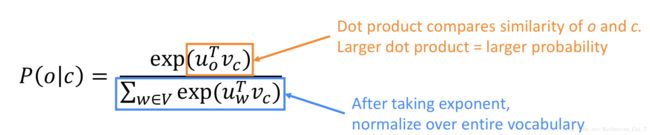
和当w为上下文词时的向量![]() 。为什么要用两个向量?更容易进行优化,在最终对每个单词生成向量的时候,将这两个向量进行平均化求值即可。则对于中心词c来说,其上下文为o出现的概率为:
。为什么要用两个向量?更容易进行优化,在最终对每个单词生成向量的时候,将这两个向量进行平均化求值即可。则对于中心词c来说,其上下文为o出现的概率为:
我们需要求的参数θ其实就是每个单词的那两个向量。如果词汇表大小为V,每个单词用d维向量进行表示,则这个参数θ就是一个2V×d维的向量。
按正常思路的话,应该是用梯度下降法进行最优参数θ的求解,但是很可惜,这种方法对凸目标函数来说是有效的,在我们这个问题中,目标函数非凸,因此梯度下降法失效。换个思路,对这个参数θ的求解,涉及到两个模型:SG(skip gram)用中心词预测上下文词和CBOW(continuous bag of words)用上下文词预测中心词。下面重点介绍skip gram算法(题外话:叫skip gram的原因是区别于bigram,这个算法是只要在窗口中即可,没有临近的要求,可以跳过几个词)。
Skip gram这个算法其实非常简单,是一个简单的单隐层神经网络,使用隐层的权重矩阵作为每个单词对应的词向量,整个网络用于计算每个词成为中心词的上下文的概率。很显然,训练语料是word pair,word pair中的第一个词是中心词,即输入,第二个词是其窗口中的中心词,即输出。举个例子,"The quick brown fox jumps over the lazy dog."这句话,如果把窗口设为2的话,中心词为brown时对应的word pair是(brown, the)、(brown, quick)、(brown, fox)、(brown, jumps)。如果网络训练比较好的话,输入brown,应该是the、quick、fox、jumps这四个词对应的位1,其余位为0。对于brown这个词来说,上下文窗口为2,整个网络要训练4次。因此,可以看出,如果两个词的上下文非常相似,则这两个词对应的词向量应该非常相近,也就是说,是同义词或近义词。
p.s. 在给定窗口中上下文词距离中心词的位置远近其实是对训练有影响的。在Mikolov的另一篇论文中有提到说,skipgram对每个中心次来说从随机减小采样的窗口,以此来“give less weight to the distant words by sampling less from those words in our training examples”
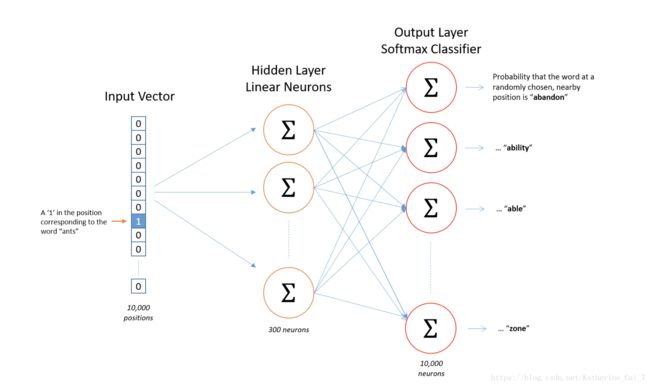
很显然,不可能把一个text string原封不动的作为输入喂给网络,需要找一种方法来对这个text string进行表示。为了解决这个问题,引入一个固定长度为V的词汇表,每一位代表一个词,则一个string用一个one-hot向量表示,维度为V。网络的输出也是一个one-hot向量,维度也是V。但是实质上网络的输出向量并不是由非0即1组成的向量,而是一系列的浮点数,是一个概率分布。每次训练的时候,对结果的衡量可以用交叉熵损失函数,计算这个概率分布和真正的one-hot输出向量的交叉熵值。整个skip gram的网络结构图如下:
隐层神经元是没有激活函数的,但是最终的输出层有一个softmax激活函数。这是因为,在典型的神经网络中,输入是一个稠密向量,将这个稠密向量和权重矩阵线性相乘,用激活函数来使结果变得非线性。而对于这个问题来说,输入并不是一个稠密向量,而是一个one-hot向量,隐层的目的只是为了选择这个词对应的词向量,没有任何非线性操作,因此不需要使用激活韩式。假设我们想用一个300维的向量去表示一个单词,则隐层的神经元数量为300。词汇表大小为10000,则隐层的权重矩阵是10000×300的,每行表示一个单词。如果把隐层的权重矩阵用W表示,输入的one-hot向量用x表示,则隐层的操作就是x·W,这个操作其实就是一个lookup操作,选出x中为1的在W中对应的行,即选出x中为1的那个词对应的词向量。
如果就按最原始的,不带任何trick的训练方法来解的话,整个网络的参数量应该是2×300×10000 = 6M个参数,这个参数量是巨大的,这个网络太大,训练基本是不可行的!在这么大的网络上使用梯度下降进行参数求解的话会很慢很慢,而且面对这么大的参数量,为了避免过拟合,需要使用大量的样本去训练。为了解决这个问题,提出三种方法,如下:
1)将常用词组作为一个"word",减小词汇表的大小。比如像“Boston Globe”这个词组,是美帝的一家报社的名称,词组的含义和“Boston”和“Globe”都相差太多,有理由把这个词组视为单独的一个“word”。这里就涉及到词组检测(phrase detection)的技术,在paper里只关注由两个词构成的词组,但是其实可以用同样的方法扩展到长度更长的词组。具体方法如下:计算任意两个词共现的次数,若候选词组中这两个词共现的次数和词组中单个词出现的次数十分接近,然后剔除掉常用词防止挖掘出类似“this is”这类的词组出现,由此完成词组的挖掘。
2)对频繁词进行子采样来减小训练样本数。还是拿“The quick brown fox jumps over the lazy dog”这个例子来说,在生成的训练语料中会出现类似(fox, the)这样的词对,这个the对于fox的含义毛贡献都没有,the在很多词的上下文中都出现过,为了学习the这个词所需的样本数要远远少于训练语料所提供的词对数量。子采样的含义就是说,对于训练语料中出现的每个词,都存在一定的概率将这个词从文本中删除,而不影响整个文本的语义,这个概率的大小与这个词的词频有关。这里涉及到一个采样率的概念,对于词![]() 来说,该词在整个语料中出现的占比为
来说,该词在整个语料中出现的占比为![]() ,用
,用![]() 表示该词被保留的概率,则
表示该词被保留的概率,则![]() 的公式如下:
的公式如下:
对于这个公式,有几个比较有意思的性质:
①当![]() 值为1.0时,
值为1.0时,![]() <= 0.0026,即某词如果出现的占比小于等于0.26%,这个词一定会被保留,只有当词的占比高于0.26%时才有被采样的概率。
<= 0.0026,即某词如果出现的占比小于等于0.26%,这个词一定会被保留,只有当词的占比高于0.26%时才有被采样的概率。
②当![]() 值为0.5时,
值为0.5时,![]() 值为0.00746
值为0.00746
③当![]() 值为0.033时,
值为0.033时,![]() 值为1,即如果一个文本全由一个词构成,则被保留的可能性为3.3%。
值为1,即如果一个文本全由一个词构成,则被保留的可能性为3.3%。
3)使用负采样,每个训练样本只修改模型的一小部分权重,而不是全部的权重。在负采样中,随机选取几个“negative”词(一般对于小数据集来说为5-20个,对于大数据集来说为2-5个)和一个“positive”词进行权重矩阵的更新(真的输出为1,为positive词,其余全为0,为negative词)。词向量只有在其作为input的一个样本的时候才会更新,负样本影响的是输出层的权重。如果是5+1的话,则只有6×300=1800个参数,加上隐层的300个参数,则一共有2100个参数需要更新,比原本的3M要小多了。至于选哪些negative词,要根据unigram分布来决定,与词频![]() 有关,词频越大,越容易被选出来做负样本,做负样本的概率公式如下:
有关,词频越大,越容易被选出来做负样本,做负样本的概率公式如下:
其中那个3/4次幂是根据经验设定的。
上边描述的三种方法并不是互斥的,在google的实现代码里这三种方法都有进行实现。这里只是说明了skip gram的具体实现原理和一些trick。至于CBOW模型,同理,只不过是训练样本的构成不一样而已,不再赘述。总体来说,SG在性能上要优于CBOW,用较大的数据集和较少的epoch,可以取得较好的效果,而且在速度上有所提升。