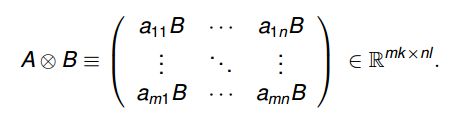SLAM笔记（一）SLAM中的数学基础概览

SLAM笔记系列系慕尼黑工业大学读书笔记，途中参考半闲居士，白巧克力亦唯心的博客加深理解，在此感谢两位。

1. 群

1.1群的定义

群G是一个集合加上这个集合的操作/运算。群需要具备封闭性，结合律，有单位元/幺元，有逆元这四个条件：

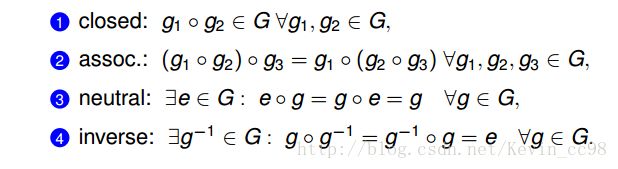
1. 2 群的矩阵表示

可以在群和矩阵之间建立单映射关系R:
R: G -> GL(n)
这种映射关系关系叫群同态.

用矩阵表示群是因为这样能更好地分析群的更抽象的性质，比如旋转群：群的逆元是矩阵的逆，就是反着转；幺元就是不转的矩阵；两个旋转矩阵相聚合又是一个新的旋转矩阵。

1.3. 常用群

1> 一般线性群(general linear matrix): GL(n) G L ( n )
满足： det(A)≠0 d e t ( A ) ≠ 0

2> 特殊线性群(special linear matrix): SL(n) S L ( n )
满足： det(A)=1 d e t ( A ) = 1

3> 仿射群 affine group A(n):
表示

L:Rn−>Rn L : R n − > R n

的关系：

L(x)=Ax+b,b∈Rn,A∈GL(n) L ( x ) = A x + b , b ∈ R n , A ∈ G L ( n )

4> 正交群 orthogonal group O(n):
点积下：

O(n)=Q∈GL(n)|QTQ=I,QQT=I O ( n ) = Q ∈ G L ( n ) | Q T Q = I , Q Q T = I

另外一种定义是

<Qx,Qy>=<x,y>,Q∈O(n) < Q x , Q y >=< x , y > , Q ∈ O ( n )

<Qx,Qy>=xTQTxQy=xTy < Q x , Q y >= x T Q x T Q y = x T y

因此有 QTQ=I Q T Q = I
也有 det(QTQ)=(det(Q))2=I d e t ( Q T Q ) = ( d e t ( Q ) ) 2 = I
则 det(Q) d e t ( Q ) = 1或-1
注意:
正交群的矩阵Q是矩阵与矩阵转置 相乘为单位矩阵。
这和 特殊线性群矩阵行列式为1是不同的。
他们有重叠关系却没有包含关系。
5> 特殊正交群(旋转群）
如果正交群的Q满足det(Q) = 1,则称Q为特殊正交群，即旋转群SO(n)，或者称之为李群（Lie group）。当然我们更常用R代表旋转群的元素。

特殊正交群SO(3)是正交的特殊线性群。

5>欧几里得群E(n)：
欧几里得群E(n) 是仿射群的子集，区别是欧几里得群的将一般线性矩阵 A∈GL(n) A ∈ G L ( n ) 转换为 R∈O(n) R ∈ O ( n ) 正交矩阵
其矩阵形式 ：

如果R为特殊正交矩阵SO(n)，则对应的欧式群称为特殊欧式群SE(n)；而SE(3)则是常见的rigid-body motions（刚体运动）

2.空间变换

三维的旋转群SO(3)可以由欧拉角、旋转矩阵、四元数等来表示。三维的旋转和位移即使SE(3

1>四元数

参考 SLAM笔记（八）-再谈四元数

2>欧拉角

欧拉角由滚转角-俯仰角-偏航角（roll-pitch-yaw）组成，但会遇到万向锁情况。

3>旋转矩阵

三维旋转可以直观表述为绕某一向量n进行角度为 θ θ 的旋转
表述为矩阵为

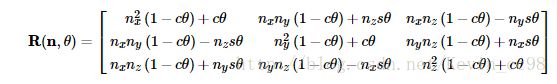
（2-1）

其中 cθ c θ , sθ s θ 分为 cosθ,sinθ c o s θ , s i n θ 。
对某一向量a = [x,y,z]进行旋转，只需要左乘R即可。
二维旋转，即对向量a = [x, y] 绕z轴进行旋转 θ θ ，则对a左乘向量(可手动旋转向量得证)：

R=[cosθsinθ−sinθcosθ] R = [ c o s θ − s i n θ s i n θ c o s θ ]

3 李群与李代数:

参见SLAM笔记-再谈李代数

3.4.刚体变换的李群

刚体群的变换（rigid body SE(3) translation ）如下：

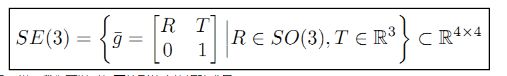
和上边同理，我们也可得到刚体变换的李群：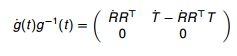
用 ŵ (t),v(t) w ^ ( t ) , v ( t ) 替换:

将 g−1 g − 1 放到右边：

因此g(t)在t周围的近似：

我们称 ξ̂  ξ ^ 为twist。怎么理解呢，就是又有角速度又有线速度，就好像钻头旋转着前进。
现在可以得到刚体变换SE(3)对应的李代数：

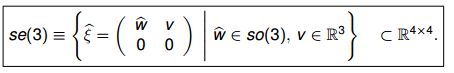
前面so(3)用3x3矩阵表达，实际元素只有3个；此处se(3)成4x4矩阵表达，但实际元素只有六个。因此可以定义一个 ∧,∨ ∧ , ∨ 来在向量表示和矩阵表示之间进行转换:

对于se(3)的向量表示，有的论文中前三维为平移，后三维为旋转，有的论文中则反过来，前三维旋转，后三维平移。
旋转变换so(3),SO(3)同理.
参照上面，可得se(3)的指数映射：

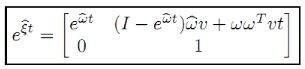
同理，对每一个SO(3)元素能在se(3)中找到一个对应的矩阵O，但可能有很多se(3)元素与之对应（只要so(3)的角度相差 2π 2 π ）

用刚体变换可以将世界坐标系中的点 X0 X 0 变换到相机坐标系X(t)：

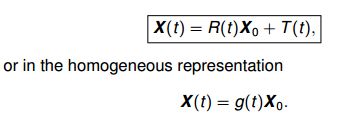
各种论文里涉及到的求解位姿矩阵时的非线性最小二乘优化（牛顿法，LM法），其中增量都是在单位矩阵处的tangent space se(3)上计算:

获得的增量(即相邻位姿变换关系)通过指数映射映射回多面体SE(3)上。通过这种方式，能够避免奇异点，保证很小的变换矩阵也能够表示出来。(《Scale Drift-Aware Large Scale Monocular SLAM》。)

3.5李代数其他部分

1>位移
对于运动中的相机，在帧t1上三维点X(t1)到帧t2对应点X(t2)的空间变换可用g(t1,t2)表示:

X(t2)=g(t1,t2)X(t1) X ( t 2 ) = g ( t 1 , t 2 ) X ( t 1 )

而转换回来则是：

X(t1)=g(t2,t1)X(t2) X ( t 1 ) = g ( t 2 , t 1 ) X ( t 2 )

上面两式左右分别相乘得到：

g(t1,t2)g(t2,t1)=I g ( t 1 , t 2 ) g ( t 2 , t 1 ) = I

2>速度
对于X(t) = gX(0)，对其求导得到速度：

而中间部分

正好是李代数。所以se(3)李代数描述的是位姿变化的相对速度

或

也能看出so(3)描述的是旋转速度。

伴随矩阵：
当另外一个观察者A从它所在的某一帧观察现在相机B时，其相对位姿为： Y(t)=gxyX(t) Y ( t ) = g x y X ( t ) 则有：

则A中观察到的B中某点速度为：

其中 V̂ y V ^ y 成为伴随矩阵

4.关于SLAM中常见群、空间变换的总结：

4.1常见群之间的关系

SO(n)⊂O(n)⊂GL(n) S O ( n ) ⊂ O ( n ) ⊂ G L ( n )

SL(n)⊂GL(n) S L ( n ) ⊂ G L ( n )

SE(n)⊂E(n)⊂A(n)⊂SL(n+1) S E ( n ) ⊂ E ( n ) ⊂ A ( n ) ⊂ S L ( n + 1 )

4.2 变换关系

欧式变换/刚体变换
(3D中6自由度，3旋转，3位移；体积不变)

[R0t1] [ R t 0 1 ]

相似变换(3D中7自由度)

[sR0t1] [ s R t 0 1 ]

相对欧式变换多了一个伸缩因子，对一个向量空间进行平移、旋转、缩放得到新的向量空间。
组成相似群Sim(n)；在坐标轴上进行同时的缩放。
结构的体积会变；仍然保持线条、平面等夹角不变，当然平行性也得到保护。

仿射变换:(3D中12自由度，A矩阵 9自由度，t有3自由度)

[A0t1] [ A t 0 1 ]

对应于仿射群A(n)：矩阵中A可逆，代表一般线性群。
表示一个向量空间进行一次线性变换，再进行一个平移，变换为另一个向量空间。
线条、平面等的夹角变化，仍然保持线条、平面的平行性；

射影变换(3D中15自由度)
也叫（三维空间平面上的）单应变换，也叫投影变换（projective transformation）

[Cedv] [ C d e v ]

目前接触到的最一般的 线性变换，其中C，d,e,v没有限制，只要满秩。当v不为0时，对整个矩阵除以v，则能看出该变换矩阵有15自由度（9(A)+3(v)+3(t)）。能保持平面相切和相交，点共线、共面的性质。

附录：

1.Kronecker product:

2. 矩阵A的栈 AS A S ：

矩阵的列向量 a1 a 1 ,…, an a n 组成的长向量 [a1,,,an]T [ a 1 , , , a n ] T ；引入它是因为可将下式左边转换成右边：

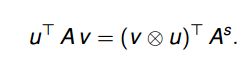
3.分层三维重建

分层三维重建，如下图所示，就是指从多幅二维图像恢复欧几里德空间的三维结构时，不是从图像一步到欧几里德空间下的三维结构，而是分步分层地进行。即先从多幅图像的对应点重建射影空间下的对应空间点(即射影重建：projective reconstruction)，然后把射影空间下重建的点提升到仿射空间下(即仿射重建：affine reconstruction)，最后把仿射空间下重建的点再提升到欧几里德空间（或度量空间: metric reconstruction）

reference(部分内容摘自原文):

1.http://www.cnblogs.com/gaoxiang12/p/5137454.html
2.http://www.cnblogs.com/gaoxiang12/p/5120175.html
3.http://blog.csdn.net/heyijia0327/article/details/50446140
4.http://download.csdn.net/detail/heyijia0327/9388031 (资料下载)