双目标定（二）单目标定基本原理

主体思路，先处理纯二维平面的畸变问题（此处略过），矫正图片后，再来求解相机内外参数。基本思路是求得每个标定板对应的单应矩阵，再联合优化所有标定板数据得到相机内参矩阵，再得到每个标定板对应的外参。

1. 标定板平面到像平面的单应矩阵H

，则对于每个棋盘格，可以得到一个标定板平面到当前图像平面的单应矩阵Hi，实际上这个单应矩阵Hi汇总了标定板平面到相机成像平面的旋转平移以及相机内参信息。
现在，我们已知每幅标定板图的单应矩阵H

2.求解相机内参矩阵

对一幅标定板图片上的标定板坐标上的一点$P=[X,Y,0,1{]}^T$由于

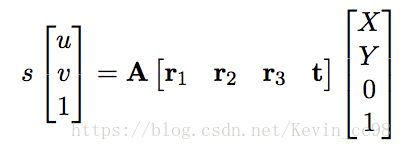
（1）

A为相机内参
实际上，由于H是二维对应关系，而标定板平面Z轴对应为0，所以：$H=[h1,h2,h3]=A[r_1,r_2,t]$,
由于R是正交矩阵，所以r1,r2正交，即r1和r2的模相同，而且点积为0,即：
$$r_1^T{r}_2=0$$
$$||r_1||=||r_2||$$
用h1，h2,替换r1,r2，则有：

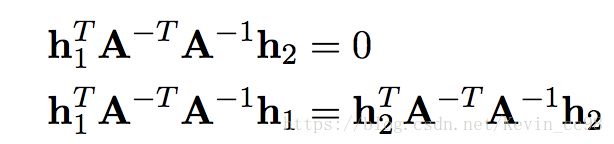
令$B=A{A}^{-1}$,则可以将上述式子化简为：

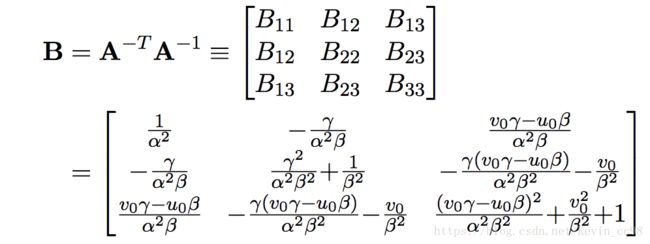
B是对称矩阵，所以可以用6个元素表示B的有效元素，则上述式子又可以表示为：

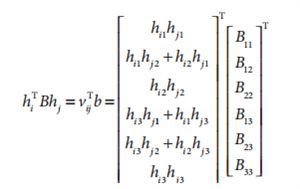
因此之前由r1,r2正交得到的式子可以转化为：

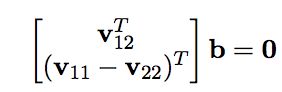
将所有标定板图像都压栈到一起，最小二乘法可以求出b。

求得b，也就是求出B，也即得到内参矩阵A。

3. 求解每个 标定板对应的外参数

根据第一个式子转换得到：

其中：
$\lambda =||A^{-1}{h}_1||=||A^{-1}{h}_2||$
就得到每个标定板平面坐标系对相机坐标系的旋转平移向量

4.最小二乘解最终的内参矩阵

通过以上方式得到最初的A和$R_i,t_i$后，考虑到观测时不可避免的噪声，所以用最小二乘方法，将所有N张图上每张图d个点的观测量用最小二乘方法解：
$$\sum _i^N\sum _j^d=m_{ij}-M(A,R_i,t_i,D_i)$$
其中$M(A,R_i,t_i,D_i)$为（1）,即投影矩阵。
用高斯牛顿法对以上进行求解。
此处，之前的格点大小就派上用场了，比如OpenCV中认为左上角的格点为b标定板平面坐标系的原点，则其他格点的三维坐标依次是：$(j\ast size,k\ast size,0)$

5.考虑畸变

一般情况下，我们先计算畸变双目标定（一）单目标定与矫正的基本介绍，然后再通过4的最小二乘估计内参矩阵。但正如张定友论文中[1]所介绍的，这种方法的收敛速度太小，所以他提出直接最小二乘求解以下包括径向畸变、内参和$R_i,t_i$在内的所有参数（他不考虑切向畸变）。其中内参和$R_i,t_i$的初始估计可用3部分的方法得到，而径向畸变可用普通径向畸变方法求解，或者直接令为0.

6.单目标定的整个流程

• 拍摄一系列含有标定板的图像
• 找出图像中的角点/格点
• 得到每张图像格点之间的匹配关系
• 求解最初的相机内参A和标定板坐标系到世界坐标系的旋转平移$R_i,t_i$
• 得到径向畸变（和切向畸变）
• 再次最小二乘联合优化内参A和$R_i,t_i$

7.双目标定流程

双目标定先得到在左侧标定板坐标系中各个格点位置，通过左侧相机的$R_i,t_i$转换到相机坐标系，再根据$R_{lr},t_{lr}$转换到右侧相机坐标系，并使得两侧的投影误差最小。在OpenCV的实现中，也是用高斯牛顿法的最小二乘方法来优化最后的结果。

for( i = 0; i < nimages; i++ )
    {
        for( j = 0; j < boardSize.height; j++ )
            for( k = 0; k < boardSize.width; k++ )
                objectPoints[i].push_back(Point3f(k*squareSize, j*squareSize, 0));
    }
///...
    double rms = stereoCalibrate(objectPoints, imagePoints[0], imagePoints[1],
                    cameraMatrix[0], distCoeffs[0],
                    cameraMatrix[1], distCoeffs[1],
                    imageSize, R, T, E, F,
                    CALIB_FIX_ASPECT_RATIO +
                    CALIB_ZERO_TANGENT_DIST +
                    CALIB_USE_INTRINSIC_GUESS +
                    CALIB_SAME_FOCAL_LENGTH +
                    CALIB_RATIONAL_MODEL +
                    CALIB_FIX_K3 + CALIB_FIX_K4 + CALIB_FIX_K5,
                    TermCriteria(TermCriteria::COUNT+TermCriteria::EPS, 100, 1e-5) );

Reference

Zhang Z. A flexible new technique for camera calibration[J]. IEEE Transactions on pattern analysis and machine intelligence, 2000, 22(11): 1330-1334.