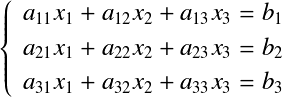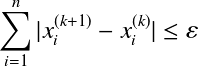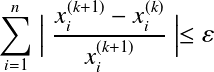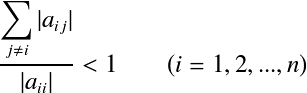【数值计算】数值解析--联立一次方程组：迭代法
雅可比迭代法
当
较大时，上一篇介绍的高斯消去法将会非常耗时(
)。本篇将介绍，通过选取一个合适的初始值，反复迭代计算，逐渐趋近方程组解的方法，称之为迭代法。下文将对最基本的迭代法—雅可比(Jacobi)迭代法进行讲解。
假设有如下所示3元联立方程组：
若系数行列的对角成分
，则可知
把 
设为初始值，按照上式依次计算
。 当
足够大时，
逐渐向解收敛。当方程组为n元联立1次方程组时，解表示如下
其中，
。
以上求解的方法便是雅可比迭代法。通过对比和
的值，判断两者之差是否是在允许误差范围内，可以检验解是否收敛。使用绝对误差的收敛条件判断如下。
同时，相对误差的收敛条件为，
这里的
是允许误差，大小自定。当迭代次数为时，计算量为
。
然而，迭代法最大的难题是如何确定收敛条件。可以通过上述的迭代式导出收敛条件。首先，把迭代式做如下变形。
当迭代次数是一个足够大的数
时，下式成立。
由这两个公式可以导出：
是
步的误差， 
是步的误差。也就是说，每迭代一次，误差增大
倍。由此，为了使得解收敛，要是得：
使用系数行列式可以表示成，
根据上式，系数行列
的各行对角元素的绝对值比非对角元素的绝对值的和大时，判断收敛。 这样的条件称作对角占优(diagonal dominant)。
雅可比迭代法代码实现
C++代码实现示例如下
/*!
* (Jacobi iterative method)
* @param[inout] A n×n系数行列和n×1的常数项(b)合并后的n×(n+1)增广行列．
* @param[in] n n元联立一次方程组
* @param[inout] max_iter 最大迭代数(返回实际迭代次数)
* @param[inout] eps 允许误差(返回实际误差)
* @return 1:成功,0:失败
*/
int JacobiIteration(vector< vector > &A, int n, int &max_iter, double &eps)
{
vector x(n, 0.0); // 初始值设为0
vector y(n, 0.0);
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 代入当前值，计算下次的候选解
for(int i = 0; i < n; ++i){
y[i] = A[i][n];
for(int j = 0; j < n; ++j){
y[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
y[i] /= A[i][i];
}
// 收敛判定
e = 0.0;
for(int i = 0; i < n; ++i){
e += fabs(y[i]-x[i]); // 绝对误差
//e += fabs((y[i]-x[i])/y[i]); // 相对误差
}
if(e <= eps){
break;
}
swap(x, y);
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = y[i];
}
return 1;
} 高斯・塞德尔迭代法
上述的雅可比迭代法只使用了
步的
值求解
的值。然而，依照 
顺序计算时， 求
时的
， 求
值时的
已经计算出来了，不妨直接使用最新计算出的分量值进行计算，这种方法就是高斯・塞德尔迭代法(Gauss-Seidel iteration method)。
例如，3元联立1次方程组的迭代式如下，
收敛判定条件及系数行列式判断条件与雅可比法相同。只是，收敛所需的迭代次数比雅可比法要少很多。
高斯・塞德尔迭代法的代码实现
雅可比法中为了存储
和
这两个变量，特别配置了2个数组， 高斯・塞德尔法由于只存储最新获得的值，只用一个数组足以。以下是这种方法的C++示例。
/*!
* (Gauss Seidel iterative method)
* @param[inout] A
* @param[in] n
* @param[inout] max_iter
* @param[inout] eps
* @return 1:成功,0:失败
*/
int GaussSeidel(vector< vector > &A, int n, int &max_iter, double &eps)
{
vector x(n, 0.0); // 初始值设为0
double tmp;
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 代入当前值，计算之后的候补值
e = 0.0;
for(int i = 0; i < n; ++i){
tmp = x[i];
x[i] = A[i][n];
for(int j = 0; j < n; ++j){
x[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
x[i] /= A[i][i];
e += fabs(tmp-x[i]); // 绝对误差
//e += fabs((tmp-x[i])/tmp); // 相对误差
}
// 收敛判定
if(e <= eps){
break;
}
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = x[i];
}
return 1;
} SOR法
使用雅可比法，高斯・塞德尔法各步所得的
と
，加速收敛的方法称作逐次加速缓和法(SOR法:Successive Over-Relaxation method)。
使用每一步计算的
，由下式计算下一步的值
，
这里的
是加速系数，通常，
。使用SOR法设定的值可以达到解快速收敛的目的。当然，如何获得一个最合适的加速系数也是这个方法的难点。
SOR法的实现
SOR法的C++安装如下。
/*!
* (SOR法:Successive Over-Relaxation)
* @param[inout] A
* @param[in] n
* @param[in] w 加速系数 ([0,2])
* @param[inout] max_iter
* @param[inout] eps
* @return 1:成功,0:失败
*/
int SOR(vector< vector > &A, int n, double w, int &max_iter, double &eps)
{
vector x(n, 0.0); // 初期值设为0
double tmp;
double e = 0.0;
int k;
for(k = 0; k < max_iter; ++k){
// 代入当前值，计算之后的候补值
e = 0.0;
for(int i = 0; i < n; ++i){
tmp = x[i];
x[i] = A[i][n];
for(int j = 0; j < n; ++j){
x[i] -= (j != i ? A[i][j]*x[j] : 0.0);
}
x[i] /= A[i][i];
x[i] = tmp+w*(x[i]-tmp);
e += fabs(tmp-x[i]); // 绝对误差
//e += fabs((tmp-x[i])/tmp); // 相对误差
}
// 收敛判定
if(e <= eps){
break;
}
}
max_iter = k;
eps = e;
for(int i = 0; i < n; ++i){
A[i][n] = x[i];
}
return 1;
}
参考文献
|