数值计算方法实验
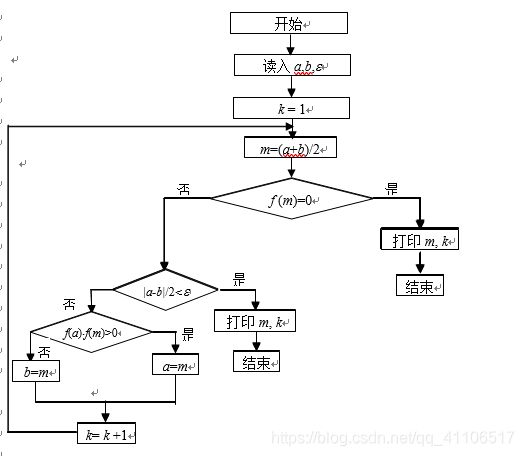
1.给定下述算法框图,用逐步扫描法和二分法求方程x5+3x-1=0的最小正根,要求准确到1/2×10-2。
要求:
(1) 取步长h=1,先用逐步扫描法编程搜索一个隔根区间,将搜索到的隔根区间打印输出;
(2) 然后对该区间使用二分法求方程的满足精度要求的根,每二分一次,用新生成区间长度的一半作为是否二分结束的判断条件;
(3) 要求步长h和精度ε从键盘输入;
(4) 输出每一次二分过程所得到的区间端点ak、bk以及区间中点xk的信息,最后打印输出满足精度要求的方程根的近似值。
源代码:
#include
#include
using namespace std;
int main(){
double x,e,a,b,m,A,h,y,f;
int k;
printf("请输入步长h和精度e:\n");
scanf("%lf%lf",&h,&e);
A = 0;
y = pow(A,5)+3*A-1;
x = x+h;
f = pow(x,5)+3*x-1;
while(f*y > 0){ //求隔根区间
y = f;
x = x+h;
f = pow(x,5)+3*x-1;
}
printf("隔根区间:(%.3lf,%.3lf)\n",x-h,x);
k = 1;a = x-h;b = x; //a为左端点,b为右端点
m = (a+b)/2;
while(1){ //二分
printf("a:%.3lf,b:%.3lf,中点:%.3lf\n",a,b,(a+b)/2);
f = pow(m,5)+3*m-1;
if(f == 0){
printf("m:%.3lf,k:%d\n",m,k);
break;
}
else{
if(abs(a-b)/2 < e){
printf("m:%.3lf,k:%d\n",m,k);
break; //满足精度要求退出循环
}
else{ //更换a,b的值
if( (pow(a,5)+3*a-1)*f > 0){
a = m;
}
else{
b = m;
}
k = k+1;
}
}
m = (a+b)/2; //继续二分
}
return 0;
} 2.用迭代法、牛顿迭代法和双点弦截法求解方程x=e-x在x=0.5附近的一个根,要求精确到小数点后五位。
要求:
(1) 在同一个程序里面将三种算法编程实现;
(2) 精度ε要求从键盘输入;
(3) 将三种算法的每一步迭代计算结果打印输出,最后输出满足精度要求的方程的根;
(4) 根据计算结果,比较三种算法的收敛速度。
源代码:
#include
#include
using namespace std;
void DD(double e){
double x=0.5,ch = 1000;
int count=0;
printf("迭代法:\n");
while(ch > e){
printf("%d %lf\n",count++,x);
double x0 = x;
x = exp(-x); //e的-x次幂
ch = x - x0;
ch = abs(ch); //求绝对值
}
printf("%d %lf\n",count++,x);
printf("最终结果:\n %.5lf\n",x);
double x0 = x;
x = exp(-x);
}
void ND(double e){
double x=0.5,ch=1000;
int count=0;
printf("牛顿迭代法:\n");
while(ch > e){
printf("%d %lf\n",count++,x);
double x0 = x;
x = x - (x - exp(-x))/(1+x);
ch = x - x0;
ch = abs(ch);
}
printf("%d %lf\n",count++,x);
printf("最终结果:\n %.5lf\n",x);
}
void SD(double e){
double x0=0.5, x2=0.6, x1=0.6, ch=1000;
int count=0;
printf("双点弦截法:\n");
printf("%d %lf\n",count++,x0);
while( abs(x2*exp(x2)-1) > e){
printf("%d %lf\n",count++,x2);
x2 = x1 - (x1*exp(x1)-1)*(x1 - x0)/( (x1*exp(x1)-1) - (x0*exp(x0)-1));
x0 = x1;
x1 = x2;
}
printf("%d %lf\n",count++,x2);
printf("最终结果:\n %.5lf\n",x2);
}
int main(){
double e;
printf("请输入精度:\n");
scanf("%lf",&e);
DD(e); //迭代法
cout<