SVD在稀疏表示中的应用
SVD:singular value decomposition奇异值分解
在认识SVD之前,先来学习两个相关的概念:正交矩阵和酉矩阵。
如果![]() ,则n阶实矩阵A称为正交矩阵。而酉矩阵是正交矩阵往复数域上的推广。
,则n阶实矩阵A称为正交矩阵。而酉矩阵是正交矩阵往复数域上的推广。
判断正交矩阵和酉矩阵的充分必要条件是:![]() 。或者说正交矩阵和酉矩阵的共轭转置和它的逆矩阵相等。
。或者说正交矩阵和酉矩阵的共轭转置和它的逆矩阵相等。
对任意![]() 矩阵,都能被奇异值分解为
矩阵,都能被奇异值分解为
其中![]() 是的
是的![]() 正交矩阵,
正交矩阵,![]() 是
是![]() 的正交矩阵,
的正交矩阵,![]() 是由r个沿对角线从大到小排列的奇异值组成的方阵,就是矩阵的秩。奇异值分解是一种正交矩阵分解法。
是由r个沿对角线从大到小排列的奇异值组成的方阵,就是矩阵的秩。奇异值分解是一种正交矩阵分解法。
奇异值分解是根据方阵的特征值分解推导而来,特征值的几何意义,在图像处理中,上面等式的左边方阵可以看成一个变换矩阵,x看成是进空间中的
一个点,那么几何意义就是,经过该几何变换后,该点还是存在于过原点与该点的直线的上.
所以说一个方阵的特征向量就是这样一个向量,经过这种特定的变换后保持方向不变,只是长度上的伸缩而已
而在稀疏表示中使用K-SVD中更新字典原子,具体为:
1 第一步是初始化系数矩阵,而在更新系数矩阵之前,需要将字典进行初始化,只有得到字典后,才能够求稀疏表示系数,字典初始化方法有:1 直接从训练样本中挑选一些向量用于构建字典,也可以自己定义一
些方法对字典进行初始化,字典初始化后,就可以通过OMP算法,正交基追踪算法求解稀疏表示系数,当然,还有其他许多方法可以进行求解
2 对字典中的各个原子进行更新:
更新的算法还是从公式进行入手:
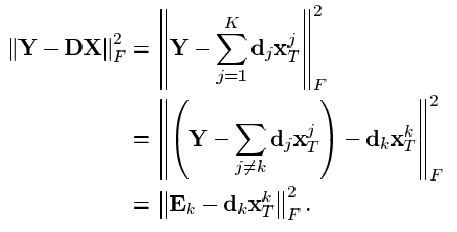
其中Y是训练样本,D是前期已经初始化的字典,X是根据初始化的字典求解的稀疏表示系数,dk是待更新的原子,xt为系数矩阵中与dk相乘的行,Y是mxn,m是行数,也是Y中一个样本向量的维度,n是样本的个数,D是字典,mxa,m是原子的维度,a是字典中原子的个数,X是axn,a是代表的是X的行数,n代表的是X的列数,X中的每一列代表的是对应Y中对应列样本的在字典D中选择的各个原子的系数,其中
最后得到上面的公式后,目标就是要该值最小,该列原子向量以及对应的系数是未知的,那么直接对Ek进行SVD分解
将得到的对应的特征值最大的特征向量作为字典的该列原子,将特征值作为系数进行,更新
这样就更新了一个原子和稀疏表示系数,重复这个步骤,直到所有原子都更新完,这样更新完得到的原子,实现了所谓的稀疏表示
需要注意的是,如果在上面的公式中直接用SVD进行更新,SVD能够找到距离Ek最近的秩为1的矩阵,单张这样得到的系数xt不稀疏,换句话说,xt与更新xt的非零元所处位置和value不一样,直观的解决办法是只保留稀疏中的非零值,由于系数在前面求解时已经实现稀疏性,因此只保留非零项,再进行SVD分解就会保留xt的稀疏解,对应的matlab代码中也有体现:
function [betterDictionaryElement,CoefMatrix,NewVectorAdded] = I_findBetterDictionaryElement(Data,Dictionary,j,CoefMatrix,numCoefUsed)
if (length(who('numCoefUsed'))==0)
numCoefUsed = 1;
end
%只取稀疏矩阵中与j列原子相关的,且非零的系数的位置
%Dictionary为MxA,CoefMatrix为AxN,与Dictionary中第j列相关的只是CoefMatrix中的第j行,因为只有CoefMatrix中的
%第j行才会与Dictionary中的第j列的元素相乘,才能够有交集
%同时这里只取非零的值,是为了保持稀疏性
relevantDataIndices = find(CoefMatrix(j,:)); % the data indices that uses the j'th dictionary element.
if (length(relevantDataIndices)<1) %(length(relevantDataIndices)==0)
ErrorMat = Data-Dictionary*CoefMatrix;
ErrorNormVec = sum(ErrorMat.^2);
[d,i] = max(ErrorNormVec);
betterDictionaryElement = Data(:,i);%ErrorMat(:,i); %
betterDictionaryElement = betterDictionaryElement./sqrt(betterDictionaryElement'*betterDictionaryElement);
betterDictionaryElement = betterDictionaryElement.*sign(betterDictionaryElement(1));
CoefMatrix(j,:) = 0;
NewVectorAdded = 1;
return;
end
NewVectorAdded = 0;
%取tmpCoefMatrix中的所有relevantDataIndices对应的列,列的个数就是数组relevantDataIndices的长度
%tmpCoefMatrix(j,:)置0是为因为为了求解,所以要置0
%Data(:,relevantDataIndices)只取data对应的relevantDataIndices的列,是因为只有这些列是与Dictionary第
%j列原子相关,因此
tmpCoefMatrix = CoefMatrix(:,relevantDataIndices);
tmpCoefMatrix(j,:) = 0;% the coeffitients of the element we now improve are not relevant.
%这里的errors就是上面的Ek,稍有不同的是,这里只选取了Y中与字典中第j个原子相关的列
errors =(Data(:,relevantDataIndices) - Dictionary*tmpCoefMatrix); % vector of errors that we want to minimize with the new element
% % the better dictionary element and the values of beta are found using svd.
% % This is because we would like to minimize || errors - beta*element ||_F^2.
% % that is, to approximate the matrix 'errors' with a one-rank matrix. This
% % is done using the largest singular value.
%svds(errors,1)的意思是对errors进行奇异值分解,分解后只保留对应特征值最大的左边向量,特征值,右边向量
%如果参数1变成2就是保留左边特征值最大的前2个左边向量,右边向量和前2个特征值,依次类推
%svds分解得到的是对应的维度为Ax1的向量:betterDictionaryElement
%以及1x1的特征值:singularValue,维度为errors的列x1的向量:betaVector
%singularValue*betaVector'其实也就是对新求得到的原子betterDictionaryElement
%上relevantDataIndies位置处元素的系数,用公式表示就是:
%errors = betterDictionaryElement*singularValue*betaVector'
%各个向量大小从左到右依次是AxB = Ax1 * 1*1 * (B*1)'
%从上面这行公式也不难看出,这里所谓的稀疏性,就是通过前面OMP只取非零项
%以及这里只取特征向量最大的值对应的行向量,列向量来实现
[betterDictionaryElement,singularValue,betaVector] = svds(errors,1);
CoefMatrix(j,relevantDataIndices) = singularValue*betaVector';% *signOfFirstElem然后再重复上面的步骤m次,将字典每个原子迭代更新m次,直到迭代完成,训练数据Y对应的原子和稀疏表示系数就得到了;完整的ksvd代码:
function [Dictionary,output] = KSVD(...
Data,... % an nXN matrix that contins N signals (Y), each of dimension n.
param)
% =========================================================================
% K-SVD algorithm
% =========================================================================
% The K-SVD algorithm finds a dictionary for linear representation of
% signals. Given a set of signals, it searches for the best dictionary that
% can sparsely represent each signal. Detailed discussion on the algorithm
% and possible applications can be found in "The K-SVD: An Algorithm for
% Designing of Overcomplete Dictionaries for Sparse Representation", written
% by M. Aharon, M. Elad, and A.M. Bruckstein and appeared in the IEEE Trans.
% On Signal Processing, Vol. 54, no. 11, pp. 4311-4322, November 2006.
% =========================================================================
% INPUT ARGUMENTS:
% Data an nXN matrix that contins N signals (Y), each of dimension n.
% param structure that includes all required
% parameters for the K-SVD execution.
% Required fields are:
% K, ... the number of dictionary elements to train
% numIteration,... number of iterations to perform.
% errorFlag... if =0, a fix number of coefficients is
% used for representation of each signal. If so, param.L must be
% specified as the number of representing atom. if =1, arbitrary number
% of atoms represent each signal, until a specific representation error
% is reached. If so, param.errorGoal must be specified as the allowed
% error.
% preserveDCAtom... if =1 then the first atom in the dictionary
% is set to be constant, and does not ever change. This
% might be useful for working with natural
% images (in this case, only param.K-1
% atoms are trained).
% (optional, see errorFlag) L,... % maximum coefficients to use in OMP coefficient calculations.
% (optional, see errorFlag) errorGoal, ... % allowed representation error in representing each signal.
% InitializationMethod,... mehtod to initialize the dictionary, can
% be one of the following arguments:
% * 'DataElements' (initialization by the signals themselves), or:
% * 'GivenMatrix' (initialization by a given matrix param.initialDictionary).
% (optional, see InitializationMethod) initialDictionary,... % if the initialization method
% is 'GivenMatrix', this is the matrix that will be used.
% (optional) TrueDictionary, ... % if specified, in each
% iteration the difference between this dictionary and the trained one
% is measured and displayed.
% displayProgress, ... if =1 progress information is displyed. If param.errorFlag==0,
% the average repersentation error (RMSE) is displayed, while if
% param.errorFlag==1, the average number of required coefficients for
% representation of each signal is displayed.
% =========================================================================
% OUTPUT ARGUMENTS:
% Dictionary The extracted dictionary of size nX(param.K).
% output Struct that contains information about the current run. It may include the following fields:
% CoefMatrix The final coefficients matrix (it should hold that Data equals approximately Dictionary*output.CoefMatrix.
% ratio If the true dictionary was defined (in
% synthetic experiments), this parameter holds a vector of length
% param.numIteration that includes the detection ratios in each
% iteration).
% totalerr The total representation error after each
% iteration (defined only if
% param.displayProgress=1 and
% param.errorFlag = 0)
% numCoef A vector of length param.numIteration that
% include the average number of coefficients required for representation
% of each signal (in each iteration) (defined only if
% param.displayProgress=1 and
% param.errorFlag = 1)
% =========================================================================
if (~isfield(param,'displayProgress'))
param.displayProgress = 0;
end
totalerr(1) = 99999;
if (isfield(param,'errorFlag')==0)
param.errorFlag = 0;
end
if (isfield(param,'TrueDictionary'))
displayErrorWithTrueDictionary = 1;
ErrorBetweenDictionaries = zeros(param.numIteration+1,1);
ratio = zeros(param.numIteration+1,1);
else
displayErrorWithTrueDictionary = 0;
ratio = 0;
end
if (param.preserveDCAtom>0)
FixedDictionaryElement(1:size(Data,1),1) = 1/sqrt(size(Data,1));
else
FixedDictionaryElement = [];
end
% coefficient calculation method is OMP with fixed number of coefficients
if (size(Data,2) < param.K)
disp('Size of data is smaller than the dictionary size. Trivial solution...');
Dictionary = Data(:,1:size(Data,2));
return;
elseif (strcmp(param.InitializationMethod,'DataElements'))
Dictionary(:,1:param.K-param.preserveDCAtom) = Data(:,1:param.K-param.preserveDCAtom);
elseif (strcmp(param.InitializationMethod,'GivenMatrix'))
Dictionary(:,1:param.K-param.preserveDCAtom) = param.initialDictionary(:,1:param.K-param.preserveDCAtom);
end
% reduce the components in Dictionary that are spanned by the fixed
% elements
if (param.preserveDCAtom)
tmpMat = FixedDictionaryElement \ Dictionary;
Dictionary = Dictionary - FixedDictionaryElement*tmpMat;
end
%normalize the dictionary.
Dictionary = Dictionary*diag(1./sqrt(sum(Dictionary.*Dictionary)));
Dictionary = Dictionary.*repmat(sign(Dictionary(1,:)),size(Dictionary,1),1); % multiply in the sign of the first element.
totalErr = zeros(1,param.numIteration);
% the K-SVD algorithm starts here.
for iterNum = 1:param.numIteration
% find the coefficients
if (param.errorFlag==0)
%CoefMatrix = mexOMPIterative2(Data, [FixedDictionaryElement,Dictionary],param.L);
CoefMatrix = OMP([FixedDictionaryElement,Dictionary],Data, param.L);
else
%CoefMatrix = mexOMPerrIterative(Data, [FixedDictionaryElement,Dictionary],param.errorGoal);
CoefMatrix = OMPerr([FixedDictionaryElement,Dictionary],Data, param.errorGoal);
param.L = 1;
end
replacedVectorCounter = 0;
rPerm = randperm(size(Dictionary,2));
for j = rPerm
[betterDictionaryElement,CoefMatrix,addedNewVector] = I_findBetterDictionaryElement(Data,...
[FixedDictionaryElement,Dictionary],j+size(FixedDictionaryElement,2),...
CoefMatrix ,param.L);
Dictionary(:,j) = betterDictionaryElement;
if (param.preserveDCAtom)
tmpCoef = FixedDictionaryElement\betterDictionaryElement;
Dictionary(:,j) = betterDictionaryElement - FixedDictionaryElement*tmpCoef;
Dictionary(:,j) = Dictionary(:,j)./sqrt(Dictionary(:,j)'*Dictionary(:,j));
end
replacedVectorCounter = replacedVectorCounter+addedNewVector;
end
if (iterNum>1 & param.displayProgress)
if (param.errorFlag==0)
output.totalerr(iterNum-1) = sqrt(sum(sum((Data-[FixedDictionaryElement,Dictionary]*CoefMatrix).^2))/prod(size(Data)));
disp(['Iteration ',num2str(iterNum),' Total error is: ',num2str(output.totalerr(iterNum-1))]);
else
output.numCoef(iterNum-1) = length(find(CoefMatrix))/size(Data,2);
disp(['Iteration ',num2str(iterNum),' Average number of coefficients: ',num2str(output.numCoef(iterNum-1))]);
end
end
if (displayErrorWithTrueDictionary )
[ratio(iterNum+1),ErrorBetweenDictionaries(iterNum+1)] = I_findDistanseBetweenDictionaries(param.TrueDictionary,Dictionary);
disp(strcat(['Iteration ', num2str(iterNum),' ratio of restored elements: ',num2str(ratio(iterNum+1))]));
output.ratio = ratio;
end
Dictionary = I_clearDictionary(Dictionary,CoefMatrix(size(FixedDictionaryElement,2)+1:end,:),Data);
if (isfield(param,'waitBarHandle'))
waitbar(iterNum/param.counterForWaitBar);
end
end
output.CoefMatrix = CoefMatrix;
Dictionary = [FixedDictionaryElement,Dictionary];
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% findBetterDictionaryElement
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [betterDictionaryElement,CoefMatrix,NewVectorAdded] = I_findBetterDictionaryElement(Data,Dictionary,j,CoefMatrix,numCoefUsed)
if (length(who('numCoefUsed'))==0)
numCoefUsed = 1;
end
relevantDataIndices = find(CoefMatrix(j,:)); % the data indices that uses the j'th dictionary element.
if (length(relevantDataIndices)<1) %(length(relevantDataIndices)==0)
ErrorMat = Data-Dictionary*CoefMatrix;
ErrorNormVec = sum(ErrorMat.^2);
[d,i] = max(ErrorNormVec);
betterDictionaryElement = Data(:,i);%ErrorMat(:,i); %
betterDictionaryElement = betterDictionaryElement./sqrt(betterDictionaryElement'*betterDictionaryElement);
betterDictionaryElement = betterDictionaryElement.*sign(betterDictionaryElement(1));
CoefMatrix(j,:) = 0;
NewVectorAdded = 1;
return;
end
NewVectorAdded = 0;
tmpCoefMatrix = CoefMatrix(:,relevantDataIndices);
tmpCoefMatrix(j,:) = 0;% the coeffitients of the element we now improve are not relevant.
errors =(Data(:,relevantDataIndices) - Dictionary*tmpCoefMatrix); % vector of errors that we want to minimize with the new element
% % the better dictionary element and the values of beta are found using svd.
% % This is because we would like to minimize || errors - beta*element ||_F^2.
% % that is, to approximate the matrix 'errors' with a one-rank matrix. This
% % is done using the largest singular value.
[betterDictionaryElement,singularValue,betaVector] = svds(errors,1);
CoefMatrix(j,relevantDataIndices) = singularValue*betaVector';% *signOfFirstElem
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% findDistanseBetweenDictionaries
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function [ratio,totalDistances] = I_findDistanseBetweenDictionaries(original,new)
% first, all the column in oiginal starts with positive values.
catchCounter = 0;
totalDistances = 0;
for i = 1:size(new,2)
new(:,i) = sign(new(1,i))*new(:,i);
end
for i = 1:size(original,2)
d = sign(original(1,i))*original(:,i);
distances =sum ( (new-repmat(d,1,size(new,2))).^2);
[minValue,index] = min(distances);
errorOfElement = 1-abs(new(:,index)'*d);
totalDistances = totalDistances+errorOfElement;
catchCounter = catchCounter+(errorOfElement<0.01);
end
ratio = 100*catchCounter/size(original,2);
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% I_clearDictionary
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function Dictionary = I_clearDictionary(Dictionary,CoefMatrix,Data)
T2 = 0.99;
T1 = 3;
K=size(Dictionary,2);
Er=sum((Data-Dictionary*CoefMatrix).^2,1); % remove identical atoms
G=Dictionary'*Dictionary; G = G-diag(diag(G));
for jj=1:1:K,
if max(G(jj,:))>T2 | length(find(abs(CoefMatrix(jj,:))>1e-7))<=T1 ,
[val,pos]=max(Er);
Er(pos(1))=0;
Dictionary(:,jj)=Data(:,pos(1))/norm(Data(:,pos(1)));
G=Dictionary'*Dictionary; G = G-diag(diag(G));
end;
end;
