TensorFlow学习笔记——实现经典LeNet5模型

TensorFlow实现LeNet-5模型

前言

今天学习使用TensorFlow搭建LeNet-5神经网络。也许一些刚入门的同学看到这个标题，就已经蒙了，啥是TensorFlow，啥是LeNet-5，没有关系，接下来就先理清楚这些概念，然后真正的一步一步实现搭建。

一、什么是TensorFlow？

TensorFlow是目前深度学习的一门框架，也是现在很热门、很多人使用的一门框架，他是编写深度学习算法时会用到的一种框架，它封装了很多类和函数，省去了我们要从最基层开始编写的时间。那为什么叫TensorFlow呢，可以拆开来理解，Tensor就是张量的意思，Flow就是流动，那么合起来就是张量在流动？这样可能还是很抽象，你可以把张量理解为多维的数组，如下图所示：

在TensorFlow中，所有的数据都可以借助张量的形式来表示。

而流动就是张量数据沿着边在不同的节点间流动并发生转化，如下图所示：

所以理解了啥是TensorFlow之后，更要清楚剩下的两个概念：计算图（Computation Graph）和会话（Session）

1. 计算图

   在编程的时候，碰到一些晦涩难懂的算法时，我们经常会画一个程序流程图来帮助我们理解，因为有图就比较直观，在程序流程图中，比如菱形表示判断，长方形是处理等等，计算图和流程图有着类似的功能。计算图中不同的形状的节点就代表着不同的运算。

   所以理解TensorFlow的计算过程可以用一个计算图来表示，你可以先把计算图理解为一个程序的流程图，在计算图上就能直观的看到数据的计算流程。上面的动图就是一个计算图。

2. Session

   就是用户使用TensorFlow时的交互式接口，他有定义一个类叫Session类，Session类提供了run（）方法来执行计算图，也就是你搭建好你的计算图之后，他是死的，你得让他动起来，Flow起来，就得使用会话让他运行。

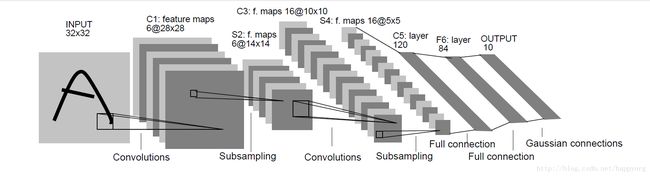
二、什么是LeNet-5？

LeNet-5是一个简单的卷积神经网络，是用于手写字体的识别的一个经典CNN，CNN可看这里

前向传播过程如下：

• INPUT层

  这是神经网络的输入，输入图像的尺寸统一为32×32。

• C１层

  输入图片：32×32

  卷积核大小：5×5

  卷积核种类：6

  输出feature map大小：28×28

  神经元数量：28×28×6

  可训练参数：（5×5+1) × 6（每个滤波器5×5=25个参数和一个bias参数，一共6个滤波器）

• S２层

  输入：28×28

  采样区域：2×2

  采样种类：6

  输出feature Map大小：14×14（28/2）

  神经元数量：14×14×6

• C３层

  输入：14×14×6

  卷积核大小：5×5

  卷积核种类：16

  输出feature Map大小：10×10 （(14-5+1)=10）

• S４层

  输入：10×10

  采样区域：2×2

  采样种类：16

  输出feature Map大小：5×5（10/2）

  神经元数量：5×5×16=400

• C５层

  输入：S4层的全部16个单元特征map（与s4全相连）

  卷积核大小：5×5

  卷积核种类：120

  输出feature Map大小：1×1（5-5+1）

• F６层

  输入：c5 120维向量

  计算方式：计算输入向量和权重向量之间的点积，再加上一个偏置，结果通过sigmoid函数输出。

  有84个神经元

  可训练参数:84×(120+1)=10164

• OUTPUT层

  Output层也是全连接层，共有10个神经元，分别代表数字0到9，且如果节点i的值为0，则网络识别的结果是数字i

三、搭建过程（代码详解）

在这一小节，我们仿照LeNet-5的思路，将他用TensorFlow的代码写出来，并且可以用这个模型来解决MNIST手写体识别问题，也就是说，我们要做的事情就是用TensorFlow代码，写出LeNet-5。

首先导入一些常用的库，以及引入MNIST数据集，就是用代码来实现下载数据集，而不是去自己下载：

处理后的每一张图片是一个长度为784的一维数组，这个数组中的元素对应了图片像素矩阵中的每一个数字（28×28=784）。因为神经网络的输入是一个特征向量，所以在此把一张二维图像的像素矩阵放到一个一维数组中可以方便tensorflow将图片的像素矩阵提供给神经网络的输入层。

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
# 下载数据集到当前目录，并且新建文件夹MNIST_data
# input_data.read_data_sets函数生成的类会自动将MNIST数据集划分为train, validation和test三个数据集
mnist = input_data.read_data_sets("./MNIST_data", one_hot=True)

接着设置一些超参数，如果还不太清楚超参数概念，可以先去这里看看

batch_size = 100 
learning_rate = 0.01
learning_rate_decay = 0.99
max_steps = 30000

接下来才是重头戏，搭建LeNet-5。再来清楚下LeNet-5，看下我们到底要写多少个卷积层、多少个池化层、多少个全连接层等等：

# 需要定义的神经网络，以及我们的命名
卷积层1	C1-conv
池化层2	S2-max_pool
卷积层3	C3-conv
池化层4	S4-max_pool
全连接5	layer5-full1
全连接6	layer6-full2

C1-conv是第一个卷积层，应用了32个5×5的卷积核，所以最后得到32个特征图：

# 创建第一个卷积层，得到特征图大小为32@28x28
# 这行代码指定了第一个卷积层作用域为C1-conv，在这个作用域下有两个变量conv1_weights和conv1_biases
    with tf.variable_scope("C1-conv",reuse=resuse):
    	# tf.get_variable共享变量
    	# [5, 5, 1, 32]卷积核大小为5×5×1，有32个
    	# stddev正太分布的标准差
        conv1_weights = tf.get_variable("weight", [5, 5, 1, 32],
                             initializer=tf.truncated_normal_initializer(stddev=0.1))
        # tf.constant_initializer初始化为常数，这个非常有用，通常偏置项就是用它初始化的
        conv1_biases = tf.get_variable("bias", [32], initializer=tf.constant_initializer(0.0))
        # strides：卷积时在图像每一维的步长，这是一个一维的向量，长度4
        # padding=’SAME’，表示padding后卷积的图与原图尺寸一致，激活函数relu()
        conv1 = tf.nn.conv2d(input_tensor, conv1_weights, strides=[1, 1, 1, 1], padding="SAME")
        relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))

S2-max_pool是第一个池化层，由C1-conv层经过2×2的最大池化得到：

# 创建第一个池化层，池化后的结果为32@14x14
    # tf.name_scope的主要目的是为了更加方便地管理参数命名。
    # 与 tf.Variable() 结合使用。简化了命名
    with tf.name_scope("S2-max_pool",):
    	# ksize：池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，
    	# 因为我们不想在batch和channels上做池化，所以这两个维度设为了1
    	# strides：窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]
        pool1 = tf.nn.max_pool(relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")

C3-conv是第二个卷积层，由之前的S2-maxpool经过卷积操作得到，特征图有64个（也就是说这一层的卷积会提取到64种特征）

# 创建第二个卷积层，得到特征图大小为64@14x14。注意，第一个池化层之后得到了32个
    # 特征图，所以这里设输入的深度为32，我们在这一层选择的卷积核数量为64，所以输出
    # 的深度是64，也就是说有64个特征图
    with tf.variable_scope("C3-conv",reuse=resuse):
        conv2_weights = tf.get_variable("weight", [5, 5, 32, 64],
                                     initializer=tf.truncated_normal_initializer(stddev=0.1))
        conv2_biases = tf.get_variable("bias", [64], initializer=tf.constant_initializer(0.0))
        conv2 = tf.nn.conv2d(pool1, conv2_weights, strides=[1, 1, 1, 1], padding="SAME")
        relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))

S4-maxpool是第二个池化层，由C3-conv经过2×2的最大池化得到：

# 创建第二个池化层，池化后结果为64@7x7
    with tf.name_scope("S4-max_pool",):
        pool2 = tf.nn.max_pool(relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
        # get_shape()函数可以得到这一层维度信息，由于每一层网络的输入输出都是一个batch的矩阵，
        # 所以通过get_shape()函数得到的维度信息会包含这个batch中数据的个数信息
        # shape[1]是长度方向，shape[2]是宽度方向，shape[3]是深度方向
        # shape[0]是一个batch中数据的个数，reshape()函数原型reshape(tensor,shape,name)
        shape = pool2.get_shape().as_list()
        nodes = shape[1] * shape[2] * shape[3]    # nodes=3136
        reshaped = tf.reshape(pool2, [shape[0], nodes])

到此为止卷积池化就结束了，接下来是第一个全连接层layer5-full1，layer5-full1接受来自第二个池化层的3136的输出，所以这一层需要1605632个权重参数（512×3136）：

# 创建第一个全连层
    with tf.variable_scope("layer5-full1",reuse=resuse):
        Full_connection1_weights = tf.get_variable("weight", [nodes, 512],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))
        # if regularizer != None:
        tf.add_to_collection("losses", regularizer(Full_connection1_weights))
        Full_connection1_biases = tf.get_variable("bias", [512],
                                                     initializer=tf.constant_initializer(0.1))
        if avg_class ==None:
            Full_1 = tf.nn.relu(tf.matmul(reshaped, Full_connection1_weights) + \
                                                                   Full_connection1_biases)
        else:
            Full_1 = tf.nn.relu(tf.matmul(reshaped, avg_class.average(Full_connection1_weights))
                                                   + avg_class.average(Full_connection1_biases))

layer6-full2是第二个全连接层，具有10个节点接受来自第一个全连接层的512个输出，所以这一层需要5120个权重参数：

with tf.variable_scope("layer6-full2",reuse=resuse):
        Full_connection2_weights = tf.get_variable("weight", [512, 10],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))
        # if regularizer != None:
        tf.add_to_collection("losses", regularizer(Full_connection2_weights))
        Full_connection2_biases = tf.get_variable("bias", [10],
                                                   initializer=tf.constant_initializer(0.1))
        if avg_class == None:
            result = tf.matmul(Full_1, Full_connection2_weights) + Full_connection2_biases
        else:
            result = tf.matmul(Full_1, avg_class.average(Full_connection2_weights)) + \
                                                  avg_class.average(Full_connection2_biases)

在得到输出结果后，就可以对这个结果进行评估，包括平均滑动模型的设计，计算交叉熵损失，总损失，设置学习率并且使用优化器以及计算精确度等等，这部分的代码如下：

# tf.placeholder(dtype, shape=None, name=None)
x = tf.placeholder(tf.float32, [batch_size ,28,28,1],name="x-input")
y_ = tf.placeholder(tf.float32, [None, 10], name="y-input")


# L2正则化是一种减少过拟合的方法
regularizer = tf.contrib.layers.l2_regularizer(0.0001)

# 调用定义的CNN的函数
y = hidden_layer(x,regularizer,avg_class=None,resuse=False)
# 定义存储训练轮数的变量
training_step = tf.Variable(0, trainable=False)
# tf.train.ExponentialMovingAverage是指数加权平均的求法
# 可以加快训练早期变量的更新速度。
variable_averages = tf.train.ExponentialMovingAverage(0.99, training_step)
variables_averages_op = variable_averages.apply(tf.trainable_variables())

average_y = hidden_layer(x,regularizer,variable_averages,resuse=True)


# 使用交叉熵作为损失函数。这里使用
# sparse_softmax_cross_entropy_with_logits函数来计算交叉熵。因为手写体是一个长度为
# 10的一维数组，而该函数需要提供的是一个正确答案的数字，所以需要使用tf.argmax函数来
# 得到正确答案对应的类别编号
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
# 计算在当前batch中所有样例的交叉熵平均值
cross_entropy_mean = tf.reduce_mean(cross_entropy)


# 总损失等于交叉熵损失和正则化损失的和
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
# 设置指数衰减的学习率
learning_rate = tf.train.exponential_decay(learning_rate,# 基础的学习率，随着迭代的进行，更新变量时使用的学习率
                                 training_step, mnist.train.num_examples /batch_size ,
                                 learning_rate_decay, staircase=True)

# 使用tf.train.GradientDescentOptimizer优化算法来优化损失函数
train_step = tf.train.GradientDescentOptimizer(learning_rate). \
    minimize(loss, global_step=training_step)

with tf.control_dependencies([train_step, variables_averages_op]):
    train_op = tf.no_op(name='train')
crorent_predicition = tf.equal(tf.arg_max(average_y,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(crorent_predicition,tf.float32))

最后就是运行会话来训练网络了，，我们的迭代次数设置为30000，并且每1000就在验证集上抽取batch_size个数据验证模型的正确率：

# 初始化会话并开始训练过程
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(max_steps):
        if i %1000==0:
            x_val, y_val = mnist.validation.next_batch(batch_size)
            reshaped_x2 = np.reshape(x_val, (batch_size,28,28, 1))
            validate_feed = {x: reshaped_x2, y_: y_val}

            validate_accuracy = sess.run(accuracy, feed_dict=validate_feed)
            print("After %d trainging step(s) ,validation accuracy"
                  "using average model is %g%%" % (i, validate_accuracy * 100))

        x_train, y_train = mnist.train.next_batch(batch_size)

        reshaped_xs = np.reshape(x_train, (batch_size ,28,28,1))
        sess.run(train_op, feed_dict={x: reshaped_xs, y_: y_train})

训练过程截图如下，有图可知，在MNIST测试数据上，我们亲手搭建的LeNet-5神经网络可以达到很高的准确率。

所以说，虽然LeNet-5网络的结构规模比较小，但是仍然包含了卷积层、池化层、全连接层这些基本组件，后面更复杂的的网络模型也离不开这小小的组件。

四、完整源码

最后附上源代码，毕竟完整的，一键运行的东西谁都喜欢

import tensorflow as tf
import numpy as np
from tensorflow.examples.tutorials.mnist import input_data
# input_data.read_data_sets函数生成的类会自动将MNIST数据集划分为train, validation和test三个数据集
mnist = input_data.read_data_sets("./MNIST_data", one_hot=True)

batch_size = 100
learning_rate = 0.01
learning_rate_decay = 0.99
max_steps = 30000


# 输入网络的尺寸为32×32×1
def hidden_layer(input_tensor,regularizer,avg_class,resuse):
    # 创建第一个卷积层，得到特征图大小为32@28x28
    # 这行代码指定了第一个卷积层作用域为C1-conv，在这个作用域下有两个变量conv1_weights和conv1_biases
    with tf.variable_scope("C1-conv",reuse=resuse):
    	# tf.get_variable共享变量
    	# [5, 5, 1, 32]卷积核大小为5×5×1，有32个
    	# stddev正太分布的标准差
        conv1_weights = tf.get_variable("weight", [5, 5, 1, 32],
                             initializer=tf.truncated_normal_initializer(stddev=0.1))
        # tf.constant_initializer初始化为常数，这个非常有用，通常偏置项就是用它初始化的
        conv1_biases = tf.get_variable("bias", [32], initializer=tf.constant_initializer(0.0))
        # strides：卷积时在图像每一维的步长，这是一个一维的向量，长度4
        # padding=’SAME’，表示padding后卷积的图与原图尺寸一致，激活函数relu()
        conv1 = tf.nn.conv2d(input_tensor, conv1_weights, strides=[1, 1, 1, 1], padding="SAME")
        relu1 = tf.nn.relu(tf.nn.bias_add(conv1, conv1_biases))

    # 创建第一个池化层，池化后的结果为32@14x14
    # tf.name_scope的主要目的是为了更加方便地管理参数命名。
    # 与 tf.Variable() 结合使用。简化了命名
    with tf.name_scope("S2-max_pool",):
    	# ksize：池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，
    	# 因为我们不想在batch和channels上做池化，所以这两个维度设为了1
    	# strides：窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]
        pool1 = tf.nn.max_pool(relu1, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")

    # 创建第二个卷积层，得到特征图大小为64@14x14。注意，第一个池化层之后得到了32个
    # 特征图，所以这里设输入的深度为32，我们在这一层选择的卷积核数量为64，所以输出
    # 的深度是64，也就是说有64个特征图
    with tf.variable_scope("C3-conv",reuse=resuse):
        conv2_weights = tf.get_variable("weight", [5, 5, 32, 64],
                                     initializer=tf.truncated_normal_initializer(stddev=0.1))
        conv2_biases = tf.get_variable("bias", [64], initializer=tf.constant_initializer(0.0))
        conv2 = tf.nn.conv2d(pool1, conv2_weights, strides=[1, 1, 1, 1], padding="SAME")
        relu2 = tf.nn.relu(tf.nn.bias_add(conv2, conv2_biases))

    # 创建第二个池化层，池化后结果为64@7x7
    with tf.name_scope("S4-max_pool",):
        pool2 = tf.nn.max_pool(relu2, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding="SAME")
        # get_shape()函数可以得到这一层维度信息，由于每一层网络的输入输出都是一个batch的矩阵，
        # 所以通过get_shape()函数得到的维度信息会包含这个batch中数据的个数信息
        # shape[1]是长度方向，shape[2]是宽度方向，shape[3]是深度方向
        # shape[0]是一个batch中数据的个数，reshape()函数原型reshape(tensor,shape,name)
        shape = pool2.get_shape().as_list()
        nodes = shape[1] * shape[2] * shape[3]    # nodes=3136
        reshaped = tf.reshape(pool2, [shape[0], nodes])

    # 创建第一个全连层
    with tf.variable_scope("layer5-full1",reuse=resuse):
        Full_connection1_weights = tf.get_variable("weight", [nodes, 512],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))
        # if regularizer != None:
        tf.add_to_collection("losses", regularizer(Full_connection1_weights))
        Full_connection1_biases = tf.get_variable("bias", [512],
                                                     initializer=tf.constant_initializer(0.1))
        if avg_class ==None:
            Full_1 = tf.nn.relu(tf.matmul(reshaped, Full_connection1_weights) + \
                                                                   Full_connection1_biases)
        else:
            Full_1 = tf.nn.relu(tf.matmul(reshaped, avg_class.average(Full_connection1_weights))
                                                   + avg_class.average(Full_connection1_biases))

    # 创建第二个全连层
    with tf.variable_scope("layer6-full2",reuse=resuse):
        Full_connection2_weights = tf.get_variable("weight", [512, 10],
                                      initializer=tf.truncated_normal_initializer(stddev=0.1))
        # if regularizer != None:
        tf.add_to_collection("losses", regularizer(Full_connection2_weights))
        Full_connection2_biases = tf.get_variable("bias", [10],
                                                   initializer=tf.constant_initializer(0.1))
        if avg_class == None:
            result = tf.matmul(Full_1, Full_connection2_weights) + Full_connection2_biases
        else:
            result = tf.matmul(Full_1, avg_class.average(Full_connection2_weights)) + \
                                                  avg_class.average(Full_connection2_biases)
    return result



# tf.placeholder(dtype, shape=None, name=None)
x = tf.placeholder(tf.float32, [batch_size ,28,28,1],name="x-input")
y_ = tf.placeholder(tf.float32, [None, 10], name="y-input")


# L2正则化是一种减少过拟合的方法
regularizer = tf.contrib.layers.l2_regularizer(0.0001)

# 调用定义的CNN的函数
y = hidden_layer(x,regularizer,avg_class=None,resuse=False)
# 定义存储训练轮数的变量
training_step = tf.Variable(0, trainable=False)
# tf.train.ExponentialMovingAverage是指数加权平均的求法
# 可以加快训练早期变量的更新速度。
variable_averages = tf.train.ExponentialMovingAverage(0.99, training_step)
variables_averages_op = variable_averages.apply(tf.trainable_variables())

average_y = hidden_layer(x,regularizer,variable_averages,resuse=True)


# 使用交叉熵作为损失函数。这里使用
# sparse_softmax_cross_entropy_with_logits函数来计算交叉熵。因为手写体是一个长度为
# 10的一维数组，而该函数需要提供的是一个正确答案的数字，所以需要使用tf.argmax函数来
# 得到正确答案对应的类别编号
cross_entropy = tf.nn.sparse_softmax_cross_entropy_with_logits(logits=y, labels=tf.argmax(y_, 1))
# 计算在当前batch中所有样例的交叉熵平均值
cross_entropy_mean = tf.reduce_mean(cross_entropy)


# 总损失等于交叉熵损失和正则化损失的和
loss = cross_entropy_mean + tf.add_n(tf.get_collection('losses'))
# 设置指数衰减的学习率
learning_rate = tf.train.exponential_decay(learning_rate,# 基础的学习率，随着迭代的进行，更新变量时使用的学习率
                                 training_step, mnist.train.num_examples /batch_size ,
                                 learning_rate_decay, staircase=True)

# 使用tf.train.GradientDescentOptimizer优化算法来优化损失函数
train_step = tf.train.GradientDescentOptimizer(learning_rate). \
    minimize(loss, global_step=training_step)

with tf.control_dependencies([train_step, variables_averages_op]):
    train_op = tf.no_op(name='train')
crorent_predicition = tf.equal(tf.arg_max(average_y,1),tf.argmax(y_,1))
accuracy = tf.reduce_mean(tf.cast(crorent_predicition,tf.float32))


# 初始化会话并开始训练过程
with tf.Session() as sess:
    tf.global_variables_initializer().run()
    for i in range(max_steps):
        if i %1000==0:
            x_val, y_val = mnist.validation.next_batch(batch_size)
            reshaped_x2 = np.reshape(x_val, (batch_size,28,28, 1))
            validate_feed = {x: reshaped_x2, y_: y_val}

            validate_accuracy = sess.run(accuracy, feed_dict=validate_feed)
            print("After %d trainging step(s) ,validation accuracy"
                  "using average model is %g%%" % (i, validate_accuracy * 100))

        x_train, y_train = mnist.train.next_batch(batch_size)

        reshaped_xs = np.reshape(x_train, (batch_size ,28,28,1))
        sess.run(train_op, feed_dict={x: reshaped_xs, y_: y_train})