WOJ1017-Billiard Ball
大神写的太详细了，mark一下慢慢膜拜！~
http://blog.sina.com.cn/s/blog_493bff030100041r.html
There is a billiard table with acute triangle shape, and there are pockets at the three corners. A billiard ball hits the side of the table not at a
corner, it is reflected in the mirror direction. And it continues to travel on the table and we assume that the energy of this ball will not be
consumed, so the velocity of the ball is a constant number in the running process.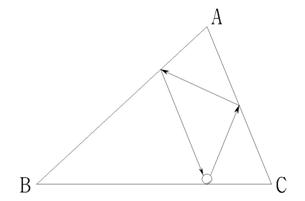
Now, you place the ball on any side of this billiard table and decide the slope of the line along which the ball starts at the origin. The trajectory
of the ball seems too complex to you, right? In order to simply this question, we will set restriction that the ball should bounce each side exactly
once and return to its start position at last. Under this restriction, can you find such trajectory that the time of ball running along it is shorter
than any other trajectories which satisfy this restriction?
输入格式
There are N test cases. The number of test cases N is given in the first line of the input file. For each test case, it contains six
integers (you are ensured that the absolute value of all the integers are less than
) which specify the vertex point coordinates of the
acute triangle.
输出格式
You should output the length of the shortest trajectory.The answer should be accurate to three fractional digits exactly one line for each test case.
样例输入
2 0 0 2 0 1 2 0 0 2 0 1 3
样例输出
3.200 3.600
（注意：题目要求小球和每边碰撞且只碰一次，最后回到出发点） 见图1
根据对称，我们可以知道
DF = D’F
DE = D”E
AD = AD’= AD”
那么，求⊿DEF的周长可以转化为求折线D’F + FE + ED”的长度
又由于两个等腰三角形⊿ADD’和⊿ADD”,有下面的角度关系：
∠D’AD” = ∠D’AB + ∠BAD + ∠DAC + ∠CAD”
= 2∠BAD + 2∠DAC = 2∠A
猜想：如果AD尽可能短，折线变成直线的话，那么所求就是最短的了。（可以想到垂线是最短的）
下面是具体的证明过程：
（1） 将D, E两点视为定点，求 DF + EF 的最小值 见图2
DF + EF的值最小，
有 ∠DFB = ∠D”FB = ∠EFA
同理，将D, F两点视为定点, 有 ∠CED = ∠AEF
将E, F两点视为定点, 有 ∠BDF = ∠CDE
见图3
A + y + z = B + z + x = C + x + y = 180°
而 A + B + C = 180°
解得：x = A, y = B, z = C
（2） 设⊿DEF为垂足三角形，那么
因为AD, BE, CF为三高，B, D, E, A四点共圆，则有：∠CED = ∠B
C, E, F, D四点共圆，则有： ∠AEF = ∠B
故： ∠CED = ∠AEF = ∠B
同理：∠BDF = ∠CDE = ∠A, ∠AFE = ∠BFD = ∠C
见图4
（3） 由(1)和(2)可知，⊿DEF为垂足三角形时，所得周长最短。
计算公式：
见图5
等腰三角形AD’D”中，
D’D” = 2 * AD * sinA ( 或2 * BE * sinB 或2 * CF * sinC )
AD = b * c * sinA / a
故D’D” = 2 * b * c * (1-cosA * cosA) / a;
#include
#include
double N_sqrt( int m0, int n0, int m1, int n1 ){
return sqrt( pow((m0 - m1), 2) + pow((n0 - n1), 2) );
}
double line( int x0, int y0, int x1, int y1, int x2, int y2){
double a, b, c, cos_a, temp;
a = N_sqrt( x0, y0, x1, y1);
b = N_sqrt( x0, y0, x2, y2);
c = N_sqrt( x1, y1, x2, y2);
cos_a = (b*b + c*c - a*a) / (2.0*b*c);
return 2*b*c*(1-cos_a*cos_a)/a;
}
int main(){
int num;
while(( scanf("%d", &num)!=EOF ) && ( num != 0 ) )
{
double l[num];
for(int i=0; i