线性代数与分解

基本的线性求解

实例

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix3f A;
   Vector3f b;
   A << 1,2,3,  4,5,6,  7,8,10;
   b << 3, 3, 4;
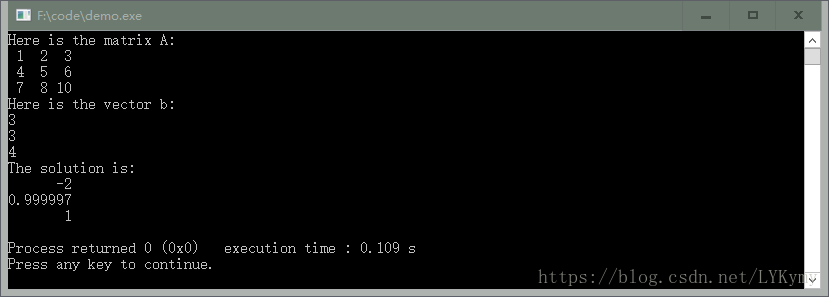
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the vector b:\n" << b << endl;
   Vector3f x = A.colPivHouseholderQr().solve(b);
   cout << "The solution is:\n" << x << endl;
}

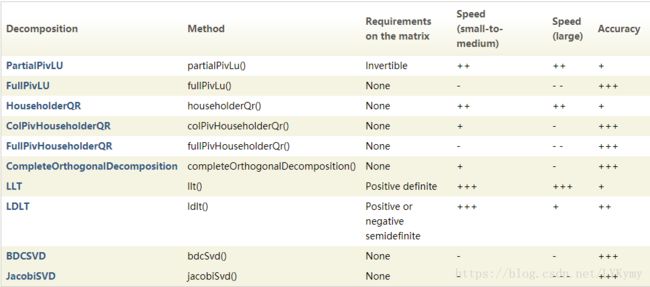
方程常用分解表 

如果您的矩阵是正定的，上面的表格说明一个很好的选择是LLT或LDLT分解。具体实例如下：

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix2f A, b;
   A << 2, -1, -1, 3;
   b << 1, 2, 3, 1;
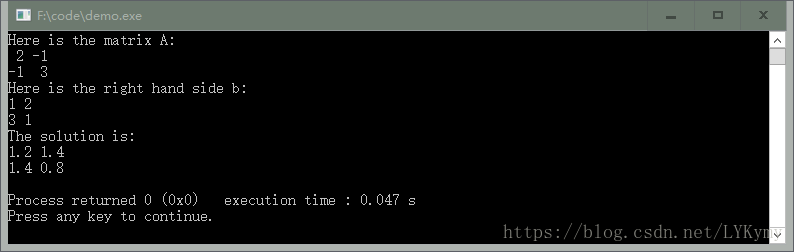
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the right hand side b:\n" << b << endl;
   Matrix2f x = A.ldlt().solve(b);
   cout << "The solution is:\n" << x << endl;
}

检查是否存在解决方案

只有您知道要允许解决方案有效的误差范围。 因此，如果您愿意，Eigen允许您自己进行此计算.

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   MatrixXd A = MatrixXd::Random(100,100);
   MatrixXd b = MatrixXd::Random(100,50);
   MatrixXd x = A.fullPivLu().solve(b);
   double relative_error = (A*x - b).norm() / b.norm(); // norm() is L2 norm
   cout << "The relative error is:\n" << relative_error << endl;
}

计算特征值与特征向量

特征值和特征向量的计算不一定会收敛，但这种收敛失败的情况非常少见。 对info（）的调用是检查这种可能性。

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix2f A;
   A << 1, 2, 2, 3;
   cout << "Here is the matrix A:\n" << A << endl;
   SelfAdjointEigenSolver eigensolver(A);
   if (eigensolver.info() != Success) abort();
   cout << "The eigenvalues of A are:\n" << eigensolver.eigenvalues() << endl;
   cout << "Here's a matrix whose columns are eigenvectors of A \n"
        << "corresponding to these eigenvalues:\n"
        << eigensolver.eigenvectors() << endl;
}

计算矩阵的逆与行列式

首先，确保你真的想要这个。 虽然逆和行列式是基本的数学概念，但在数值线性代数中，它们并不像纯数学那样受欢迎。 反向计算通常有利地由solve（）操作代替，并且行列式通常不是检查矩阵是否可逆的好方法。

虽然某些分解（如PartialPivLU和FullPivLU）提供了inverse（）和determinant（）方法，但您也可以直接在矩阵上调用inverse（）和determinant（）。 如果您的矩阵具有非常小的固定大小（最多4x4），则允许Eigen避免执行LU分解，而是使用在这种小矩阵上更有效的公式。

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix3f A;
   A << 1, 2, 1,
        2, 1, 0,
        -1, 1, 2;
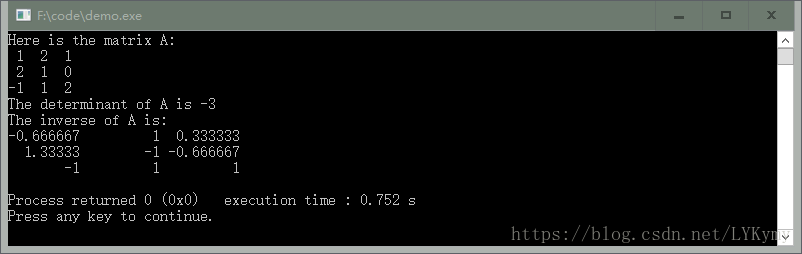
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "The determinant of A is " << A.determinant() << endl;
   cout << "The inverse of A is:\n" << A.inverse() << endl;
}

最小二乘法求解

进行最小二乘求解的最准确方法是使用SVD分解。 Eigen提供了两种实现方式。 推荐的是BDCSVD类，它可以很好地扩展到大问题，并自动回退到JacobiSVD类以解决较小的问题。 对于这两个类，他们的solve（）方法正在进行最小二乘求解。

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   MatrixXf A = MatrixXf::Random(3, 2);
   cout << "Here is the matrix A:\n" << A << endl;
   VectorXf b = VectorXf::Random(3);
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "The least-squares solution is:\n"
        << A.bdcSvd(ComputeThinU | ComputeThinV).solve(b) << endl;
}

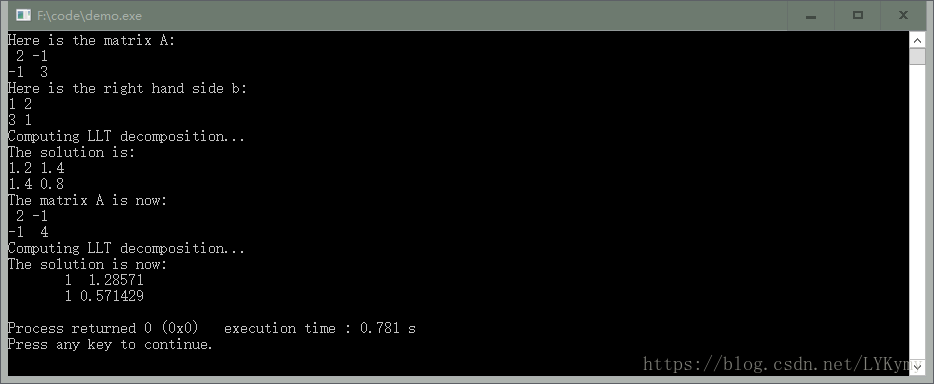
实现计算与构造的分离

有些情况下你可能想要将这两件事分开，例如，如果你在构造时不知道你想要分解的矩阵; 或者如果要重用现有的分解对象。以下两点使这成为可能：

• 所有分解都有一个默认的构造函数
• 所有分解都有一个计算（矩阵）方法来进行计算，并且可以在已经计算的分解上再次调用它，重新初始化它。

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix2f A, b;
   LLT llt;
   A << 2, -1, -1, 3;
   b << 1, 2, 3, 1;
   cout << "Here is the matrix A:\n" << A << endl;
   cout << "Here is the right hand side b:\n" << b << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is:\n" << llt.solve(b) << endl;
   A(1,1)++;
   cout << "The matrix A is now:\n" << A << endl;
   cout << "Computing LLT decomposition..." << endl;
   llt.compute(A);
   cout << "The solution is now:\n" << llt.solve(b) << endl;
}

揭示分解排名

某些分解是等级显示的，即能够计算矩阵的等级。 这些通常也是在非满秩矩阵（在正方形情况下意味着奇异矩阵）时表现最佳的分解。 在这张表上，你可以看到我们所有的分解是否是等级揭示。排名显示分解至少提供了rank（）方法。 它们还可以提供方便的方法，如isInvertible（），有些还提供了计算矩阵的内核（零空间）和图像（列空间）的方法，就像FullPivLU一样：

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix3f A;
   A << 1, 2, 5,
        2, 1, 4,
        3, 0, 3;
   cout << "Here is the matrix A:\n" << A << endl;
   FullPivLU lu_decomp(A);
   cout << "The rank of A is " << lu_decomp.rank() << endl;
   cout << "Here is a matrix whose columns form a basis of the null-space of A:\n"
        << lu_decomp.kernel() << endl;
   cout << "Here is a matrix whose columns form a basis of the column-space of A:\n"
        << lu_decomp.image(A) << endl; // yes, have to pass the original A
}

当然，任何秩计算都取决于任意阈值的选择，因为实际上没有浮点矩阵完全是秩缺陷的。 Eigen选择合理的默认阈值，这取决于分解，但通常是对角线大小乘以机器epsilon。 虽然这是我们可以选择的最佳默认值，但只有您知道应用程序的正确阈值。 您可以通过在调用rank（）之前调用分解对象上的setThreshold（）或任何其他需要使用此阈值的方法来设置此项。 分解本身，即compute（）方法，与阈值无关。 更改阈值后，无需重新计算分解。

#include 
#include 
using namespace std;
using namespace Eigen;
int main()
{
   Matrix2d A;
   A << 2, 1,
        2, 0.9999999999;
   FullPivLU lu(A);
   cout << "By default, the rank of A is found to be " << lu.rank() << endl;
   lu.setThreshold(1e-5);
   cout << "With threshold 1e-5, the rank of A is found to be " << lu.rank() << endl;
}