深度学习与PyTorch入门实战（二） 线性回归问题

2 回归问题

简单线性回归：

对数据进行线性拟合
$$y=wx+b$$
从

到

进行曲线拟合

1、目标
$$loss=\Sigma (WX+b-y{)}^2$$
求 loss 最小值，对应的 w 和 b

2、通过数据信息，对其梯度下降，在迭代过程中获得最优解（凸优化）
$$w‘=w-lr\ast dloss/dw$$

代码

import numpy as np

# loss = Σ(WX + b - y)^2
def conpute_error_for_line_given_points(b, w, points):
    totalError = 0
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        totalError += (y - (w * x + b)) ** 2
    return totalError / float(len(points))

# w` = w - lr * δloss / δw
def step_gradient(b_current, w_current, points, learningRate):
    b_gradient = 0
    w_gradient = 0
    N = float(len(points))
    for i in range(0, len(points)):
        x = points[i, 0]
        y = points[i, 1]
        b_gradient += -(2/N) * (y - ((w_current * x) + b_current))
        w_gradient += -(2/N) * x * (y - ((w_current * x) + b_current))

    new_b = b_current - (learningRate * b_gradient)
    new_w = w_current - (learningRate * w_gradient)
    return [new_b, new_w]

# Iterate to optimize
def gradient_descent_runner(points, starting_b, starting_w, learning_rate, num_iterations):
    b = starting_b
    w = starting_w
    for i in range(num_iterations):
        b, w = step_gradient(b, w, np.array(points), learning_rate)
    return [b, w]


def run():
    points = np.genfromtxt("./Deep-Learning-with-PyTorch-Tutorials/lesson04-简单回归案例实战/data.csv", delimiter=",")
    learning_rate = 0.0001
    initial_b = 0
    initial_w = 0
    num_iterations = 1000
    print("Starting gradient descent at b = {0}, m = {1}, error = {2}"
          .format(initial_b, initial_w,
                  conpute_error_for_line_given_points(initial_b, initial_w, points)))
    print("running...")
    [b, w] = gradient_descent_runner(points, initial_b, initial_w, learning_rate, num_iterations)
    print("After {0} iterations b = {1}, w = {2}, error = {3}"
          .format(num_iterations, b, w,
                  conpute_error_for_line_given_points(b, w, points)))

if __name__ == '__main__':
    run()

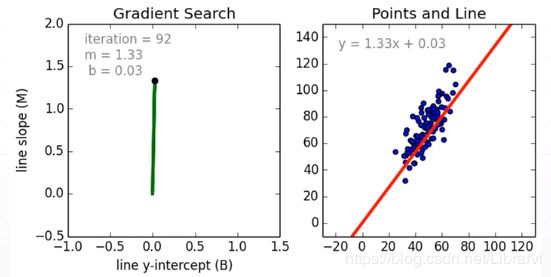
结果：