梯有N阶,上楼可以一步上一阶,也可以一次上二阶(Java实现)
组合数学和动态规划算法
欢迎查看相关动态规划问题:动态规划之:让你轻松理解背包算法
本文尝试对“走楼梯”问题做一个较为系统的解释。
代码可以自己复制出去,调试运行和理解!
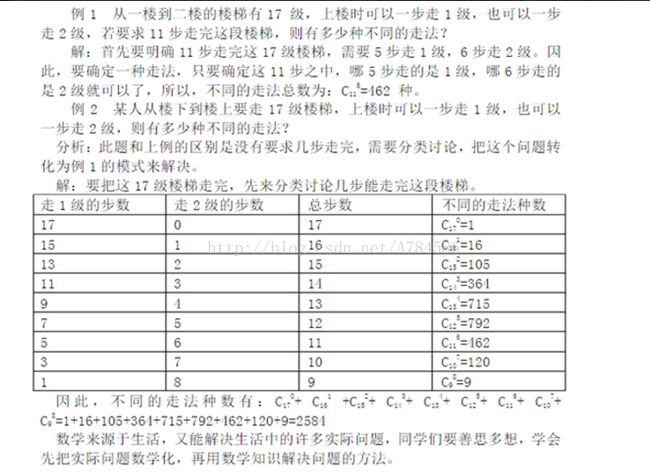
例3:一共有10级,每次可走一步也可以走两步.必须要8步走完10级楼梯. 问:一共有多少种走法?
分析:走一步的需要6次,走两步的需要2次。因此,本题是6个1、2个2的组合问题。在6个一步中,插入2个两步的,因可放在第一个1步之前,也可以放在最后一个1步之后,所以6个1步有7个空.因此,如果两个两步在一起有c(7,1)种;如果两个两步的分开来插有C(7,2)种,因此共有
c(7,1)+c(7,2)=7+21=28(种)=C(8,2)=C(8,6)
总数=8步中选2中走两步的=8步中选6个走一步的
Java编程实现:(数组迭代,动态规划,递归)
package com.test;
public classzoutaijie {
// 梯有N阶,上楼可以一步上一阶,也可以一次上二阶。编一个程序,计算共有多少种不同的走法。如果上20阶会有几种走法
public staticlongresult[]=new long[100];
public staticvoidmain(String[] args) {
result[0]=result[1]=1;
for(inti=2;i<=result.length;i++)
result[i]=-1;
//s不能太大,否则int溢出
int s =60;
//动态规划
long startTime = System.currentTimeMillis();
System.out.println("动态规划解决:"+fun1(s));
long endTime = System.currentTimeMillis();
System.out.println("动态规划解决-程序运行时间:"+(endTime-startTime)+"ms");
//数组叠加
long startTime2 = System.currentTimeMillis();
System.out.println("数组叠加实现:"+fun2(s));
long endTime2 = System.currentTimeMillis();
System.out.println("数组叠加实现-程序运行时间:"+(endTime2-startTime2)+"ms");
//递归方法
long startTime1 = System.currentTimeMillis();
System.out.println("递归方法解决:"+fun(s));
long endTime1 = System.currentTimeMillis();
System.out.println("递归方法解决-程序运行时间:"+(endTime1-startTime1)+"ms");
}
public staticlongfun(ints){
if(s==0 || s==1)
return 1;
else{
return fun(s-1)+fun(s-2);
}
}
public staticlongfun1(ints){
if(result[s]>=0) {
return result[s];
}else{
result[s]=(fun1(s-1)+fun1(s-2));
return result[s];
}
}
public staticlongfun2(ints){
long result_1[]=newlong[s+1];//注意这个要大一个,多了个第0个
result_1[0]=result_1[1]=1;
for(inti=2;i<=s;i++)
result_1[i]=result_1[i-1]+result_1[i-2];
return result_1[s];//s就是第s+1个
}
}分析:
s=48和s=60输出结果,显然数组叠加和动态规划效率高很多很多,不是一个数量级的!
变形:如果每次可以走一步,2步,3步。。。。N步,那一共有多少种?
1)这里的f(n) 代表的是n个台阶有一次1,2,...n阶的 跳法数。
2)n = 1时,只有1种跳法,f(1) = 1
3) n = 2时,会有两个跳得方式,一次1阶或者2阶,这回归到了问题(1) ,f(2) = f(2-1) + f(2-2)
4) n = 3时,会有三种跳得方式,1阶、2阶、3阶,
那么就是第一次跳出1阶后面剩下:f(3-1);第一次跳出2阶,剩下f(3-2);第一次3阶,那么剩下f(3-3)
因此结论是f(3) = f(3-1)+f(3-2)+f(3-3)
5) n = n时,会有n中跳的方式,1阶、2阶...n阶,得出结论:
f(n) = f(n-1)+f(n-2)+...+f(n-(n-1)) + f(n-n) => f(0) + f(1) + f(2) + f(3) + ... + f(n-1)
6) 由以上已经是一种结论,但是为了简单,我们可以继续简化:
f(n-1) = f(0) + f(1)+f(2)+f(3) + ... + f((n-1)-1) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2)
f(n) = f(0) + f(1) + f(2) + f(3) + ... + f(n-2) + f(n-1) = f(n-1) + f(n-1)
可以得出:
f(n) = 2*f(n-1)
7) 得出最终结论,在n阶台阶,一次有1、2、...n阶的跳的方式时,总得跳法为:
| 1 ,(n=0 )
f(n) = | 1 ,(n=1 )
也可以这样更简单:
每个台阶都有跳与不跳两种情况(除了最后一个台阶),最后一个台阶必须跳。所以共用2^(n-1)中情况
######################################################################################
猛然的一次实现:
package com.mytest.mymain;
import java.io.*;
public class Main{
public static void main(String[] args) throws Exception{
//方式1 #############
java.util.Scanner sc=new java.util.Scanner(System.in);//001
String str;
while((str=sc.nextLine())!=null){ //002
int n=Integer.parseInt(str);
long[] result=new long[n+2];
result[1]=1;
result[2]=2;
if(n==1 || n==2 ){
System.out.println(result[n]);
}else{
for(int i=3;i<=n;i++){
result[i]=result[i-1]+result[i-2];
}
System.out.println(result[n]);
}
}
//方式2 #################
/* BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String str;
while((str=br.readLine())!=null){
int n=Integer.parseInt(str);
long[] result=new long[n+2];
result[1]=1;
result[2]=2;
if(n==1 || n==2 ){
System.out.println(result[n]);
}else{
for(int i=3;i<=n;i++){
result[i]=result[i-1]+result[i-2];
}
System.out.println(result[n]);
}
}*/
}
}线下两个方式都可以通过的,但是在线上牛客网调试方式2可以,方式1就不通过,方式一和方式二仅仅只是在001和002处两处差异,其他代码完全一样。
最终找到解决办法:
把002改为:
//while(sc.hasNext()){ //003
//str=sc.nextLine();
所以在寻求统一形式编码习惯的同时需要注意一些更多的细节区别。
欢迎读者思考,评论,发表自己观点!
##################################################
经典同原理题目,斐波那数列问题实现:
递归:f(n)=f(n-1)+f(n-2),n=0,f=0;n=1,f=1;
非递归高效实现:
1.时间复杂度为O(n)
public class Solution {
public int Fibonacci(int n) {
int f_1=1;
int f_2=0;
int result=0;
if(n<=0){ return 0; }
if(n==1){ return 1; }
if(n>=2){
for(int i=2;i<=n;i++){
result=f_1+f_2;
f_2=f_1;
f_1=result;
}
}
return result;
}
}2.时间复杂度为O(logN)
利用如下数学公式:(一般要求非递归的动态规划实现,如上实现即可,这种不够实用,可做知识面储备)