【数据结构与算法】Size Balanced Tree（SBT）平衡二叉树

尺寸平衡树（SBT）平衡二叉树

---

原文链接大小平衡树（SBT）平衡二叉树

定义数据结构

struct SBT
{
    int key,left,right,size;
} tree[N];

关键：存储值，左，右：左右子树，大小：保持平衡最终要的数据，表示子树的大小

SBT树的性质

定义一个节点X，同时满足下面两个条件

(a)、x.left.size >= max(x.right.right.size, x.right.left.size)
(b)、x.right.size >= max(x.left.left.size, x.left.right.size)

即每棵子树的大小不小于其兄弟子树的大小

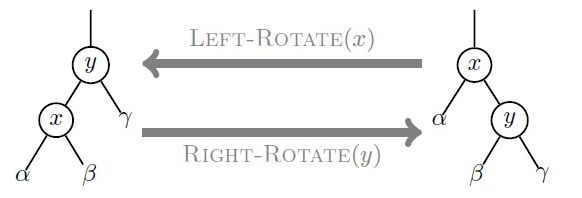
旋转

左旋伪代码：

Left-Rotate (t)
 
1     k ← right[t]
2     right[t] ← left[k]
3     left[k] ← t
4     size[k] ← size[t]
5     size[t] ← size[left[t]] + size[right[t]] + 1
6     t ← k

void left_rot(int &x)
{
    int y = tree[x].right;
    tree[x].right = tree[y].left;
    tree[y].left = x;
    tree[y].size = tree[x].size;//转上去的节点数量为先前此处节点的size
    tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
    x = y;
}

右旋伪代码：

Right-Rotate(t)
 
1     k ← left[t]
2     left[t] ← right[k]
3     right[k] ← t
4     size[k] ← size[t]
5     size[t] ← size[left[t]] + size[right[t]] + 1
6     t ← k

void right_rot(int &x)
{
    int y = tree[x].left;
    tree[x].left = tree[y].right;
    tree[y].right = x;
    tree[y].size = tree[x].size;
    tree[x].size = tree[tree[x].left].size + tree[tree[x].right].size + 1;
    x = y;
}

旋转只需要理解如何维护子树尺寸即可，旋转操作不能改变二叉查找树的基本性质

维护SBT性质（维持）

当我们插入或删除一个结点后，SBT的大小就发生了改变。这种改变有可能导致性质的（a）或（b）中被破坏。这时，我们需要用维护操作来修复这棵树.Maintain操作是SBT中最具活力的一个独特过程; Maintain（T）用于修复以T为根的SBT。调用Maintain（T）的前提条件是T的子树都已经是SBT了。
我们需要讨论的有4种情况。由于性质a和性质b是对称的，所以我们仅仅详细的讨论性质a。
第一种情况：x.left.left.size> x.right.size

即：插入（T.left，key）后A.size> R.size

1.首先执行右键Ratote（t）的

2.在这之后，有时候这棵树还不然不是一棵SBT，因为s [C]> s [B]或者s [D]> s [B]也是可能发生的。所以就有必要继续调用（T）
3.结点L的右子树有可能被连续调整，因为有可能由于性质的破坏需要再一次运行维持（L）。

第二种情况：x.left.right.size> x.right.size

在执行完插入（T.left，key）后发生B.size> R.size，这种调整要比情况1复杂一些。我们可以执行下面的操作来修复：
1，执行一次左旋操作左Ratote（L）

2，接着执行一次右旋操作右键Ratote（T）：

3，在经过两个巨大的旋转之后，整棵树就变得非常不可预料了万幸的是，子树甲; E; F; R依然是容均树，所以要依次修复L和T，Maintain（L），Maintain（T）
4，子树都已经是容均树了，但B可能还有问题，所以还要调用保持（B）

第三种情况：x.right.right.size > x.left.size
与第一种情况
相反第四种情况：x.right.left.size> x.left.size
与第二种情况相反
伪代码

Maintain (t,flag)
 
01     If flag=false then
02          If s[left[left[t]]>s[right[t]] then      //case1
03               Right-Rotate(t)
04          Else
05               If s[right[left[t]]>s[right[t]] then   //case2
06                    Left-Rotate(left[t])
07                     Right-Rotate(t)
08          Else                                   //needn’t repair
09               Exit
10     Else
11          If s[right[right[t]]>s[left[t]] then      //case1'
12               Left-Rotate(t)
13          Else
14               If s[left[right[t]]>s[left[t]] then     //case2'
15                    Right-Rotate(right[t])
16                    Left-Rotate(t)
17          Else                                    //needn’t repair
18               Exit
19     Maintain(left[t],false)                     //repair the left subtree
20     Maintain(right[t],true)                     //repair the right subtree
21     Maintain(t,false)                           //repair the whole tree
22     Maintain(t,true)                            //repair the whole tree

void maintain(int &x,bool flag)
{
    if(flag == false)//左边
    {
        if(tree[tree[tree[x].left].left].size > tree[tree[x].right].size)//左孩子的左子树大于右孩子
            right_rot(x);
        else if(tree[tree[tree[x].left].right].size > tree[tree[x].right].size)//右孩子的右子树大于右孩子
        {
            left_rot(tree[x].left);
            right_rot(x);
        }
        else return;
    }
    else //右边
    {
        if(tree[tree[tree[x].right].right].size > tree[tree[x].left].size)//右孩子的右子树大于左孩子
            left_rot(x);
        else if(tree[tree[tree[x].right].left].size > tree[tree[x].left].size)//右孩子的左子树大于左孩子
        {
            right_rot(tree[x].right);
            left_rot(x);
        }
        else return;
    }
    maintain(tree[x].left,false);
    maintain(tree[x].right,true);
    maintain(x,true);
    maintain(x,false);
}

插入

在BST插入的基础上添加一个维护操作，用来对尺寸的维护

void insert(int &x,int key)
{
    if(x == 0)
    {
        x = ++top;
        tree[x].left = tree[x].right = 0;
        tree[x].size = 1;
        tree[x].key = key;
    }
    else
    {
        tree[x].size ++;
        if(key < tree[x].key) insert(tree[x].left,key);
        else  insert(tree[x].right,key);//相同元素插入到右子树中
        maintain(x, key >= tree[x].key);//每次插入把平衡操作压入栈中
    }
}

删除

与普通维护大小域的BST删除相同。
关于无需维持的说明由sqybi：
在删除之前，可以保证整棵树是一棵SBT。当删除之后，虽然不能保证这棵树还是SBT，但是这时整树的最大深度并没有改变，所以时间复杂度也不会增加。这时，维护就显得是多余的了。

下面给出两种删除方式，一种是找前驱替换，一种是找后继替换
//后继
 

int remove(int &x,int key) 
{
    tree[x].size --;
    if(key > tree[x].key)
        remove(tree[x].right,key);
    else if(key < tree[x].key)
        remove(tree[x].left,key);
    else
    {
        //有左子树，无右子树
        if(tree[x].left != 0 && tree[x].right == 0)
        {
            int temp = x;
            x = tree[x].left;
            return temp;
        }
        else if(tree[x].right !=0 && tree[x].left == 0)
        {
            int temp = x;
            x = tree[x].right;
            return temp;
        }
        //无左子树和右子树
        else if(!tree[x].left && !tree[x].right)
        {
            int temp = x;
            x = 0;
            return temp;
        }
        //有右子树
        else //找到x右子树中最小元素，也就是找后继元素
        {
            int temp = tree[x].right;
            while(tree[temp].left) temp = tree[temp].left;
            tree[x].key = tree[temp].key;
            //tree[x].cnt = tree[temp].cnt;
            remove(tree[x].right,tree[temp].key);
        }
    }
}

//前驱

int  remove(int &x,int key)
{
    int d_key;
    //if(!x) return 0;
    tree[x].size --;
    if((key == tree[x].key)||(key < tree[x].key && tree[x].left == 0) ||
            (key>tree[x].key && tree[x].right == 0))
    {
        d_key = tree[x].key;
        if(tree[x].left && tree[x].right)
        {
            tree[x].key = remove(tree[x].left,tree[x].key+1);
        }
        else
        {
            x = tree[x].left + tree[x].right;
        }
    }
    else if(key > tree[x].key)
        d_key = remove(tree[x].right,key);
    else if(key < tree[x].key)
        d_key = remove(tree[x].left,key);
    return d_key;
}

获取最小值

直接向左子树找到最左叶子节点即可

int getmin()
{
    int x;
    for(x = root ; tree[x].left; x = tree[x].left);
    return tree[x].key;
}

获取最大值

int getmax()
{
    int x;
    for(x = root ; tree[x].right; x = tree[x].right);
    return tree[x].key;
}

前驱

int pred(int &x,int y,int key)//前驱 小于
{
    if(x == 0) return y;
    if(tree[x].key < key)//加上等号，就是小于等于
        return pred(tree[x].right,x,key);
    else return pred(tree[x].left,y,key);
}//pred(root,0,key)

注解：

if（tree [x] .key

if（tree [x] .key> = key）说明前驱在左子树，当前节点x的键值也不是其前驱，所以设定其前驱仍为y

后继

int succ(int &x,int y,int key)//后继 大于
{
    if(x == 0) return y;
    if(tree[x].key > key)
        return succ(tree[x].left,x,key);
    else return succ(tree[x].right,y,key);
}

同前驱。

求第ķ小数

int select(int &x,int k)//求第k小数
{
    int r = tree[tree[x].left].size + 1;
    if(r == k) return tree[x].key;
    else if(r < k) return select(tree[x].right,k - r);
    else return select(tree[x].left,k);
}

注解：首先该源码如果插入的数有重复数据（即树中会出现两个或多个27，这样的数据），此SBT是可以建树的，同样在查询第ķ小数上述代码也不会产生错误，但是这里需要消耗更多的存储空间（这里应该很容易明白），如果我们在数据结构中加上一个字段CNT，专门用来记录重复数据的个数，这样的话树中就没有重复数据，因为它们已经被合并了，这里需要修改的插入函数和除去函数和旋转操作，如果删除操作每次删除的是整个节点而不是CNT> 2就仅仅将cnt--而是整个删除，这样就会对尺寸造成很大的影响，这种情况的删除函数我暂时没有想好如何去写，首先可以确定思路，如果删除节点是x，它的直接或间接父亲节点的大小都需要减去x.cnt，但是我们是用的替换删除，这里怎么操作？还请哪位大牛指教，能够写出这样的删除函数。
还是先解释上面的代码，首先求 出x的左子树大小，再加上自己本身，如果这时r == k则说明x.key就是第K小数，如果r k那么说明第K小数在以x为根的左子
树上。

求元素的秩

就是求这个元素排第几

int rank(int &x,int key)//求key排第几
{
    if(key < tree[x].key)
        return rank(tree[x].left,key);
    else if(key > tree[x].key)
        return rank(tree[x].right,key) + tree[tree[x].left].size + 1;
    return tree[tree[x].left].size + 1;
}

这里就类似选择的逆操作，代码就不解释了。

#include 
#include 
#include 
#include 
#include 
#include 
#include 
#include 

总结：

SBT，树堆，红黑树，都很类似，其中SBT和树堆代码很好写，SBT只需要正确理解旋转操作，和如何维护大小域，另外就是保持函数，这个是重点，其他的操作都和BST一样了，SBT的高度是O（logn）时间，维护是O（1），所有主要操作都是O（logn）时间。

最后还请大神解决下重复数据的删除操作函数如何写（具体见求第ķ小数下的注解），欢迎指教。

原文：HTTPS：//blog.csdn.net/acceptedxukai/article/details/6921334