dfs序 与 树链剖分 例题 Distance on the tree
dfs序和熟练剖分本质上是hash,将树型结构转换成线性结构
熟练剖分是dfs序的一种
dfs序
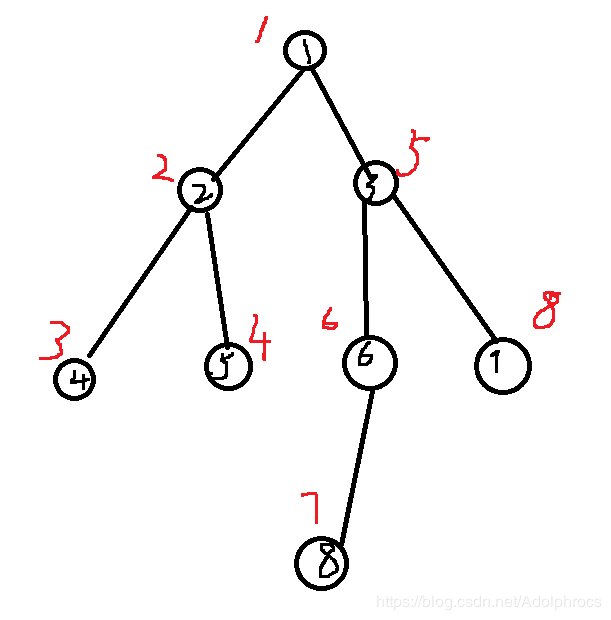
就是dfs遍历点的顺序,对于二叉树就是其中序遍历的顺序,如图红色序号
特点:一颗子树的序号是连续一段序号,比如1的左子树(2,3,4)右子树(5,6,7,8)
然后我们记录一个in[x], out[x],表示子树的开始和结束编号,具体看代码
void dfs(int x, int fa){
in[x] = ++tot;
for (x的孩子v){
dfs(v,x);
out[x] = tot;
}作用,比如将x的整个子树的值加上一个值,就可以用线段树维护(in[x], out[x])
树链剖分
类似于dfs序,但是dfs找x的孩子v时,不是随便找的,而是找重儿子,下面给出重儿子的定义
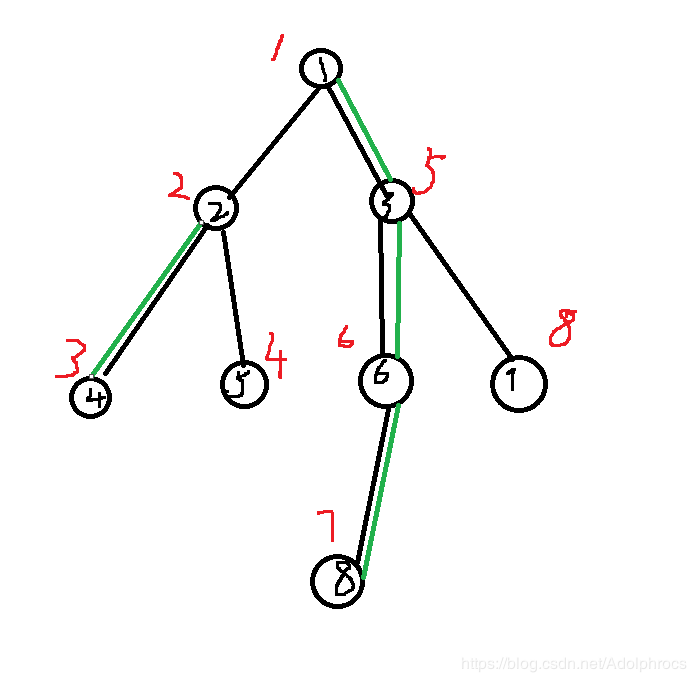
首先定义sz[x],表示以x为根的子树的大小。如上图sz[2] = 3, sz[5] = 4, sz[1] = 7
定义重儿子son[x],表示孩子种sz[]最大的一个孩子(一样大就随便取)。如上图,son[1] = 5, son[5] =6
定义重链,由重儿子连起来的点,如图绿色标的是重链,其余的是轻链
具体看代码
void dfs(int x, int fa){
sz[x] = 1;//本身加进去
son[x] = 0;//没有重儿子
for(x的孩子v){
dfs(v, x);
sz[x] += sz[v];
if (sz[v] > sz[son[x]]) son[x] = v;//sz最大的是重儿子
}
}
//当然你可以顺便把dep[],fa[]什么的顺便求出来然后求dfs序的时候,优先重儿子,顺便记录一个值top[x], 标志链的第一个节点,比如1,5,6,7的top都是1,5的top是5
例如具体看代码
void dfs1(int x, int now_top){
top[x] = now_top;
id[x] = ++tot;
if (son[x]) dfs(son[x], now_top);//优先重儿子,top和自己的top一样
for (x的孩子v){
if (v != son[x]) dfs(v, v);//轻链的top是自己
}
}作用,对于树上的两个点之间的路径可以拆分成若干条链,然后每条链序号是连续的,可以用线段树维护
具体怎么拆分成若干条链,大致就是处理完一条链,就跳到他top的上一个节点,就表示这条链处理完了
举个例子,我要算3到6的权值和,就是(2,3)+(1,2)+(1,6)
处理完(top[3],3),跳到fa[top],然后将fa[top],和另一个点作为新得区间,重复做,具体看代码
int ques_ans(int u, int v){
int f1 = top[u], f2 = top[v], ans = 0;
while (f1 != f2){//知道区间到了同一条链上
if (dep[f1] < dep[f2]){ //先做top低的,往top高的逼近
swap(u, v);
swap(f1,f2);
}
ans += query(1, n, 1, pos[f1], pos[u]); //把这段区间加上去
u = fa[f1];f1 = top[u]; //跳到top的fa
}
// 这时候已经在一条链上了
if (u == v) return ans; //在一个点,直接返回
if (dep[u] > dep[v]) swap(u, v);
return ans + query(1, n, 1, pos[son[u]], pos[v]); //把剩余的权加上
}
例题,2019南昌网络赛,J. Distance on the tree
https://nanti.jisuanke.com/t/38229
| Problem | DSM(Data Structure Master) once learned about tree when he was preparing for NOIP(National Olympiad in Informatics in Provinces) in Senior High School. So when in Data Structure Class in College, he is always absent-minded about what the teacher says. The experienced and knowledgeable teacher had known about him even before the first class. However, she didn't wish an informatics genius would destroy himself with idleness. After she knew that he was so interested in ACM(ACM International Collegiate Programming Contest), she finally made a plan to teach him to work hard in class, for knowledge is infinite. This day, the teacher teaches about trees." A tree with nn nodes, can be defined as a graph with only one connected component and no cycle. So it has exactly n-1n−1 edges..." DSM is nearly asleep until he is questioned by teacher. " I have known you are called Data Structure Master in Graph Theory, so here is a problem. "" A tree with nn nodes, which is numbered from 11to nn. Edge between each two adjacent vertexes uu and vv has a value w, you're asked to answer the number of edge whose value is no more than kk during the path between uu and vv."" If you can't solve the problem during the break, we will call you DaShaMao(Foolish Idiot) later on." The problem seems quite easy for DSM. However, it can hardly be solved in a break. It's such a disgrace if DSM can't solve the problem. So during the break, he telephones you just for help. Can you save him for his dignity? |
| input | In the first line there are two integers n,mn,m, represent the number of vertexes on the tree and queries(2 \le n \le 10^5,1 \le m \le 10^52≤n≤105,1≤m≤105) The next n-1n−1 lines, each line contains three integers u,v,wu,v,w, indicates there is an undirected edge between nodes uu and vv with value ww. (1 \le u,v \le n,1 \le w \le 10^91≤u,v≤n,1≤w≤109) The next mm lines, each line contains three integers u,v,ku,v,k , be consistent with the problem given by the teacher above. (1 \le u,v \le n,0 \le k \le 10^9)(1≤u,v≤n,0≤k≤109) |
| Ouput | For each query, just print a single line contains the number of edges which meet the condition. |
|
|
|
|
题意:给出一个树,每条边都有边权,m个查询,每次问u到v的路径上权值小于等于k的个数
题解:离线将查询按k排序,然后用线段树依次维护树链剖分上权小于k的个数
AC代码
#include
using namespace std;
const int maxn = 2e5+2;
const int maxm = 1e5+2;
struct Ques{
int l ,r, k, id;
}Q[maxm];
struct node{
int u, v, w;
}E[maxn];
int n , m, last;
bool cmp(const Ques A, const Ques B){
return A.k < B.k;
}
bool cmp2(const node A, const node B){
return A.w < B.w;
}
int Ans[maxn];
vector edge[maxn];
int sz[maxn], son[maxn], pos[maxn], tot, dep[maxn], fa[maxn], top[maxn];
void dfs(int x, int u){
sz[x] = 1;son[x] = 0;
fa[x] = u;
for (int i = 0; i< edge[x].size(); i++){
if (edge[x][i] == fa[x]) continue;
dep[edge[x][i]] = dep[x] + 1;
dfs(edge[x][i], x);
sz[x] += sz[edge[x][i]];
if (sz[edge[x][i]] > sz[son[x]]) son[x] = edge[x][i];
}
}
void dfs1(int x, int now_top) {
top[x] = now_top;
pos[x] = ++tot;
if (son[x]) dfs1(son[x], now_top);
for (int i = 0; i< edge[x].size(); i++){
if (edge[x][i] == fa[x]) continue;
if (edge[x][i] != son[x]){
dfs1(edge[x][i], edge[x][i]);
}
}
}
int tr[maxn * 4];
void add(int l , int r , int p ,int a, int b){
if (l > a || r < a) return;
if (l == a && r == a){
tr[p] = b;
return ;
}
int mid = (l +r) / 2;
if (a <= mid) add(l, mid , p * 2 , a, b);
else add(mid +1, r, p*2+1, a, b);
tr[p] =tr[p *2] + tr[p * 2+1];
}
int query(int l, int r, int p , int a, int b){
if (l > b || r < a) return 0;
if(l >= a && r <=b){
return tr[p];
}
int mid = (l +r) /2;
if (b <= mid) return query(l, mid, p * 2, a, b);
else if (a > mid) return query(mid + 1, r, p *2 + 1, a, b);
else return query(l, mid, p * 2, a, b) + query(mid+1, r, p * 2 +1, a, b);
}
int ques_ans(int u, int v){
int f1 = top[u], f2 = top[v], ans = 0;
while (f1 != f2){
if (dep[f1] < dep[f2]){
swap(u, v);
swap(f1,f2);
}
ans += query(1, n, 1, pos[f1], pos[u]);
u = fa[f1];f1 = top[u];
}
if (u == v) return ans;
if (dep[u] > dep[v]) swap(u, v);
return ans + query(1, n, 1, pos[son[u]], pos[v]);
}
int main() {
scanf("%d%d", &n, &m);
for (int i = 1; i< n;i++){
int u, v, w;
scanf("%d%d%d", &u,&v,&w);
edge[u].push_back(v);
edge[v].push_back(u);
E[i].u = u;
E[i].v = v;
E[i].w = w;
}
sort(E+1,E+n, cmp2);
dfs(1, 1);
dfs1(1, 1);
for (int i = 1; i <= m;i++){
scanf("%d%d%d", &Q[i].l, &Q[i].r, &Q[i].k);
Q[i].id = i;
}
sort(Q+1, Q+1+m, cmp);
last = 0;
for (int i =1; i<=m;i++){
for (int j = last+1; j < n; j++){
if (E[j].w > Q[i].k) break;
if (dep[E[j].u] > dep[E[j].v]) swap(E[j].u, E[j].v);
add(1, n, 1, pos[E[j].v], 1);
last = j;
}
Ans[Q[i].id] = ques_ans(Q[i].l, Q[i].r);
}
for (int i = 1; i <= m;i++){
printf("%d\n", Ans[i]);
}
return 0;
}