ProxyLessNAS

ProxyLessNAS : Direct Neural Architecture Search On Target Task And Hardware

Related Work

Proxy Tasks:

1.在小数据集上训练

2.只学习一些小的Blocks

3.只训练一小部分的Epoch

Motivation

1.基于 Proxy Tasks的NAS方法并没有考虑到诸如Latency等性能的影响

2.现存的NAS结构是采用搜索Block的方法进行Stack组成最终的网络结构，但是实际情况中，每一个Block是可以不同的

3.DARTS是一种创造性的将Architecture 和Weight联合进行SGD优化的，但是在使用Proxy Tasks学习Block进行堆叠的同时又存在GPU Consumption的方法
$$m_O^{DARTS}(x)=\underset{i=1}{\overset{N}{\Sigma }}{p}_i{o}_i(x)=\underset{i=1}{\overset{N}{\Sigma }}\frac{exp({\alpha }_i)}{{\Sigma }_{j}exp({\alpha }_j)}{o}_i(x)$$

4.Drop Path是一种可以找到紧性的高效网络结构的方法
$$m_O^{One-Shot}(x)=\underset{i=1}{\overset{N}{\Sigma }}{o}_i(x)$$

Overview

本文提出了一种Path-Level的剪枝方法

**Step 1：**直接训练一种包含所有候选Path的超参Network

**Step 2：**在训练过程中，通过引入结构化参数来学习通路的冗余性

**Step 3：**在最终获得紧性的优化结构时将具有冗余性的Path进行剪枝

存在问题：

• 随着可选Operations的增加，可选Network的Size越大，会增加GPU Memory

  • Solution：借助"Binary Connect"的思路，将Architecture Parameters二值化，在一个Run-Time中只允许一个Path被激活

• Hardware Objectives(e.g. Latency)不可微

  • 将Network Latency抽象成连续函数，利用正常的Loss进行优化
  • Reinforce-Based Algorithm

Contributions

1.直接在大型数据集上且不需要使用Proxy Task的技术进行训练和学习

2.允许在大型的候选集上进行搜索

3.打破了Block 堆叠的Network的构成方式

4.提出了对于NAS做剪枝的方案，展示了NAS与模型压缩之间的相近的关系，同时通过Path剪枝，本文的方法节约了大约一个量级的计算量

5.提出了一个基于Latency Regularization Loss的梯度下降方法以解决硬件目标问题

Method

Construction of Over-Parameterized Network

Question:为了能够进行搜索，必须要对整个超参的网络结构进行定义

解决方案：所有的Path都是混合通路，学习的是整个Network而不是Block

将Network用$N(e=m_O^1,...,e=m_O^n)$表示

• $e_i$代表一个有向无环图的一条确定的边
• $O=\{o_i\}$是一个含有$N$个初始Operations(卷积、池化、Identity、Zero)的集合
• $m_O$每条边上含有N条并行通路的一个混合操作

因此，对于一个输入$x$，混合操作$m_O$的输出结果是基于$N$条通路所形成的

Learning Binarized Path

**Question:**随着Path可选的空间逐渐扩大，Weight的运算量将不断增加

**解决方案：**二值化Path

ProxyLessNet在训练过程中，在众多的Path中，只激活一个Path，故此本文将所有的Path进行二值化处理
$$g=binarize(p_1,...,p_N)=\{\begin{array}{rlrlr}[1,0,...,0]& & with& probability& p_1\\ ...& & & & \\ [0,0,...,1]& & with& probability& P_N\end{array}$$

因此对于给定的binary gate $g$
$$m_O^{Binary}(x)=\underset{i=1}{\overset{N}{\Sigma }}{g}_i{o}_i(x)=\{\begin{array}{rlrl}{o}_1(x)& with& probability& p_1\\ ...& & & \\ o_N(x)& with& probability& p_N\end{array}$$

[说明]:此处值得注意的是$architecture$ $parameters$并没有直接包含在$m_O^{Binary}$的计算公式中，因此不能直接通过该公式对$Architecture$进行优化，下文中，借用DARTS中的方法对$Architecture$进行转换

Training Binarized Architecture Parameters

**Question：**对于以上网络的定义，就像先前的NAS，必须要解决Architecture和Weight的更新迭代问题

**解决方案：**Binary Connect–>Weight 更新Architecture

• 训练$weight$：
  • 固定Architecture参数
  • 根据公式(3)随机采样Binary Gate
  • 通过Binary Gate激活的Path利用SGD的方法在训练集上进行优化
• 训练$ArchitectureParameters$:
  • 固定$weight$
  • 重置Binary Gate
  • 在验证集上更新Architecture

[说明]:以上两个优化过程必须要交替进行

• Architecture Parameter确定时，通过砍掉具有冗余性的Path即可得到紧致性网络结构 [此处利用了Drop Path操作]，为了简化，本文采用了具有最高Path权重的Path作为基础的Architecture
  $$\frac{\partial L}{\partial {\alpha }_i}=\underset{j=1}{\overset{N}{\Sigma }}\frac{\partial L}{\partial g_j}\frac{\partial p_j}{\partial {\alpha }_i}=\underset{j=1}{\overset{N}{\Sigma }}\frac{\partial L}{\partial g_j}\frac{\partial \frac{exp({\alpha }_j)}{{\Sigma }_{k}exp({\alpha }_k)}}{\partial {\alpha }_i}=\underset{j=1}{\overset{N}{\Sigma }}\frac{\partial L}{\partial g_j}{p}_j({\delta }_{ij}-p_i)$$

**Question：**此处值得注意的是$\frac{\partial L}{\partial g_j}=o_j$,因此借助网络的反向传播算法是可以计算的但是，$o_j$是需要保存在memory中

**解决方法：**本文考虑将选择N个候选中的一个路径的任务分解为多个二进制选择任务

• Step 1:更新Architecture Parameters

• Step 2:根据多项式分布$(p_1,p_2,...p_N)$ 采样两个Path [此处利用了MASK]

  通过以上两个步骤，就可以直接将候选操作的数量由$N$降解为2.同时$path$ $weight$和$Binary$ $Gate$也要随之重置

• Step 3:利用公式$(5)$重新采样的两个Path的$Architecture$ $Parameters$进行更新

• Step 4:通过在Architecture Parameters上应用softmax来计算Path Weight，需要通过乘以比率因子来重新调整这两个更新的Architecture Parameters的值，以保持非采样路径的路径权重不变

[效果]:

• 采样Path-A:Path Weight增加
• 采样Path-B:Path Weight下降
• Other Path:Path Weight不变

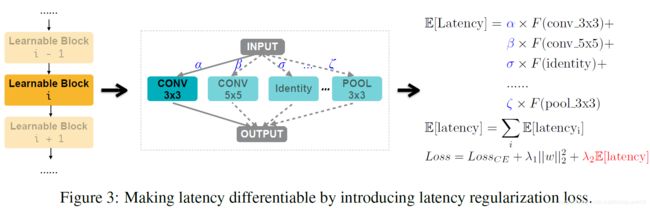
Handling Non-Differentiable hardware Metrics

Question：Latency不可微

解决方法：构建可微函数，使得网络可以通过反向传播进行SGD更新优化

• Step 1：使得Latency 可微

  假设：

  $\{o_j\}$：一个混合操作的动作候选集

  $p_j$：与$o_j$相对应的path weight,代表了选择$o_j$的概率

  ${\mathbb{E}}_{[latenc{y}_i]}$：是第$i$个Block的Latency的期望值

  $F(\dot{})$代表的是Latency 预测模型

  • $${\mathbb{E}}_{[latenc{y}_i]}={\Sigma }_j{p}_j^i\times F(o_j^i)$$

  $$\frac{\partial {\mathbb{E}}_{latenc{y}_i}}{\partial p_j^i}=F(o_j^i)$$

  因此对于整个网络来说:
  $${\mathbb{E}}_{[latency]}={\Sigma }_i{\mathbb{E}}_{[latenc{y}_i]}$$

---

Network Loss

$$Loss=Los{s}_{CE}+{\lambda }_1||w|{|}_2^2+{\lambda }_2{\mathbb{E}}_{[latency]}$$

Reinforce-Based Approach

Question:针对于Binary Gate的优化问题的解决方案

**解决方法：**ReInforce可以用于训练二值权重

具体的公式推演可以详看论文

Experience

Conclusion

• GPU prefers shallow and wide model with early pooling;
• CPU prefers deep and narrow model with late pooling.
• Pooling layers prefer large and wide kernel.
• Early layers prefer small kernel.
• Late layers prefer large kernel.

GPU

CPU:

Mobile