Python数据结构与算法(十五、字典树(又叫Trie,前缀树))
保证一周更两篇吧,以此来督促自己好好的学习!代码的很多地方我都给予了详细的解释,帮助理解。好了,干就完了~加油!
声明:本python数据结构与算法是imooc上liuyubobobo老师java数据结构的python改写,并添加了一些自己的理解和新的东西,liuyubobobo老师真的是一位很棒的老师!超级喜欢他~
如有错误,还请小伙伴们不吝指出,一起学习~
No fears, No distractions.
一、Trie
- 什么是Trie?
Trie不同于前面的树结构,是一种多叉树。Trie是一个真正的用于字典的数据结构,因为Trie树经常处理的对象大多数为字符串。
举个栗子:
a. 就拿我们以前实现的基于二分搜索树的字典为例,查询的时间复杂度是O(logn),如果有100万个条目,logn大约为20。而Trie树能够做到查询每个条目的时间复杂度和字典中一共有多少条目无关!且时间复杂度为O(w),w为单词的长度!而且大多数的单词的字符个数是小于10的,这就使得Trie在查询单词方面非常的高效。
b. 上个图吧。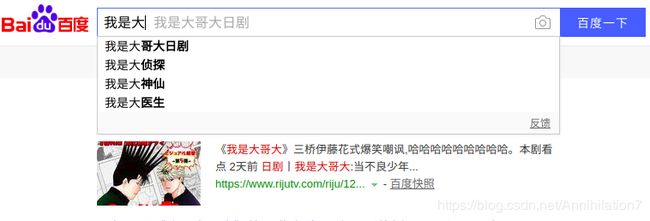
百度搜索“我是大”,你看下边蹦出来好多基于“我是大”为前缀的关键字,这也是Trie树主要的贡献之一!所以Trie树也叫“前缀树”。
二、Trie树讲解
声明:上图源自liuyubobobo老师上课的PPT,如有侵权请联系,立刻删除~
- 所有的字符串构建均从根节点出发!
- 我们最直观的理解就是对于英文字符串而言,就只有26个字母嘛,所以每个节点最多只有26个孩子节点,但是字符串里面有特殊符号怎么办?所以这里采取的办法就是用相应的next char来代表边,这样我们的孩子节点就是动态的构建,也就可以创建无数个孩子节点了,很显然通过这个边到达的就是下一个节点,所以我们的节点里面可以存放一个字典:对应的是char到next_Node的映射。(python中不一定是char,只要是能组成string的元素就行。)
- 对于pan这个单词,代表平底锅,而panda中pan是panda的前缀,如果我们的Trie中有"panda",那么如何直到到底有没有"pan"呢?因为二者的路径是一样的呀。所以在这里我们要在节点中再添加一个属性:isWord,是bool类型的,代表该Node到底是不是一个单词的标识。比如说"pan"这个单词,如果节点’n’的isWord属性是False,则代表我们的Trie树中没有"pan"这个单词,反之就是存在这个单词!
- 可以认为trie是专门为字符串所设计的集合或者是映射。
综上,我们的Trie树的节点类所包含的属性:
class Node{
bool isWord; // 代表是否是一个单词
Map<char, Node> next; // char代表两节点的边,Node则是下一个节点。
}
三、实现
还是小小的说明一下吧,大家在跑简单的测试样例或者我的测试样例的时候,要多多debug!pycharm的话调试更方便,多调试才能理解每个数据结构的在执行相关操作时的运作方式。调试确实帮助我这个菜逼很多。。
# -*- coding: utf-8 -*-
# Author: Annihilation7
# Data: 2018-12-22 15:26
# Python version: 3.6
class Node:
"""节点类"""
def __init__(self, is_word=False):
self.is_Word = is_word # 默认情况下self.is_Word为False
self.next = dict() # python是动态语言,无法指定类型,所以建立一个空字典就好了。
# 小小的说明一下,正因为无法指定类型,我们可以向我们的Trie中添加不限于英文字符的任意字符!这就是python的牛逼之处呀,其他静态编译语言
# 大多数都会写成:map 那么只能处理英文字符串了。。
class Trie:
def __init__(self):
self._root = Node()
self._size = 0 # size初始化为零
def isEmpty(self):
return self._size == 0 # 判空
def getSize(self):
return self._size # 获取树的size
def contains(self, word):
"""
判断单词word是否已经存在于树中(非递归版本)。
Params:
- word: 待查找单词
"""
cur = self._root # 从根节点开始
for character in word: # 遍历要查询的单词
cur = cur.next.get(character, None) # 找下一个节点中的字典以character为键所对应的值,没找到返回None
if cur == None:
return False # 没找到返回False
return cur.is_Word == True # 即使找到最后了,也要注意那个"pan"和"panda"的问题哦,如果此时的is_Word为True,表明真的存在这个单词,否则还是不存在!
def contains_RE(self, node, word, index):
"""
判断单词word是否已经存在于树中(递归版本)。
Params:
- node: 当前节点
- word: 待查找单词
- index: 表明此时到达word的哪个element了,即word[index]是待考察的element。
"""
if index == len(word): # 递归到底的情况,同样要注意最后一个元素的is_Word是不是真的为True
if node.is_Word:
return True
return False
dst_element = word[index] # 标记这个元素,方便大家理解后面的代码
if node.next.get(dst_element, None) is None: # 如果当前节点的next的dict键中不包含dst_element
return False # 直接返回False
return self.contains_RE(node.next[dst_element], word, index + 1) # 否则去到node的next中以dst_element为键的Node是否包含word[index + 1]
def add(self, word):
"""
向Trie中添加一个单词word,注意不是单个字符哦(课上讲的迭代版本)
Params:
- word: 待添加的单词
"""
if self.contains(word): # 先判断是否已经存在,存在直接返回就ok。
return
cur = self._root # 从根节点开始,前面也说过了,Trie的字符串全部是从根节点开始的哦
for character in word: # 遍历要添加的单词的element
if cur.next.get(character, None) is None: # 如果next_node中以character为键的值不存在
cur.next[character] = Node() # 就新建一个Node作为character的值
cur = cur.next.get(character) # 更新cur到下一个以character为边的Node,注意代码的逻辑哦,值不存在就新建,此时也是到下一个character为边的Node
# 只不过此时到达的是一个我们刚刚新建的空Node。如果存在,就直接到下一个已经存在的Node了,一点问题没有。
cur.is_Word = True # 最后注意既然是添加,所以单词尾部的element的is_Word一定要设为True,表示存在这个单词了。
self._size += 1 # 更新self._size
def add_RE(self, node, word, index):
"""
向Trie中添加一个单词word(自己理解的递归版本)
Params:
- node: 当前节点
- word: 待添加的单词
- index: 表明此时到达word的哪个element了,即word[index]是待考察的element。
"""
if index == len(word): # 递归到底的情况,注意可能涉及到更新当前节点的is_Word
if not node.is_Word: # 如果当前节点的is_Word为False
node.is_Word = True # 更新为True
self._size += 1 # 并维护self._size
return
dst_element = word[index] # 标记这个元素,方便理解后面的代码
if node.next.get(dst_element, None) is None: # 如果当前节点的next的dict键中不包含dst_element
node.next[dst_element] = Node() # 就为这个键新建一个Node
return self.add_RE(node.next[dst_element], word, index + 1) # 新建了也好,没新建也罢,都是要跑到下一个节点去看word[index + 1]这个element
# 是否存在,不存在就新建,存在就顺着往后撸。
def isPrefix(self, astring):
"""
查询是否在Trie中有单词以prefix为前缀,注意'abc'也是'abc'的前缀,另外递归版本的就不写了,甚至要比contains_RE简单
Params:
-astring: 待查询字符串
Returns:
有为True,没有返回False
"""
cur = self._root
for character in astring:
cur = cur.next.get(character, None)
if cur is None:
return False
return True # 此时就不用考虑is_Word啦,因为只要找前缀,并非确认该前缀是否真正存在与trie中
def remove(self, astring):
"""
删除Trie树中的字符串。(自己的理解,有问题还请小伙伴指出,一般的竞赛神马的也不会涉及到删除操作的。)
因为我们的Trie树只能从头往后撸,所以要先遍历一遍记录每个Node,然后反向遍历每个Node来从后往前删除,有点像单向链表哦。
Params:
- astring: 待删除的字符串
"""
# 这里不调用self.contains判断astring是否存在于Trie中了,因为这样的话多了一次遍历。
cur = self._root # 从根节点出发,准备记录
record = [cur] # 初始化record,就是根节点
# 因为如果你想删除'hello',那么'h'的信息只有根节点有,所以根节点是必须要添加进record的。
for character in astring: #遍历astring
flag = cur.next.get(character, None) # 判断Trie中到底有没有astring
if flag is None: # 如果没有,直接return就好。相比先contains判断的话少一次循环哦。
return
record.append(cur.next[character]) # 先将下一个Node添加进record中
cur = cur.next[character] # cur往后撸
if len(cur.next): # 这里是一种特殊情况:比如我们的Trie中有'pan'和'panda',但是'panda'和'pan'有着共同的路径,即p->a->n,
# 所以是不可能全部删除'p','a','n'的,因为'panda'我们并不想删除呀。
# 这里的处理反倒很简单,直接将当前cur到达的node的is_Word设为False就好啦~,'pan'就不复存在了!
cur.is_Word = False
self._size -= 1 # 便忘了删完后维护一下self._size
return
# 删除操作
string_index = len(astring) - 1 # 从后往前删,联想单链表删除操作
for record_index in range(len(record) - 2, -1, -1): # 此时record的容量应该为len(astring) + 1,因为我们一开始就添加了self._root
# 而最后一个Node是没用的,因为要删除的话只能找到目标的前一个node进行删除,所以从倒数第二个node开始向前遍历
remove_char = astring[string_index] # 记录要删除的字符,便与小伙伴理解
cur_node = record[record_index] # 记录当前的node
del cur_node.next[remove_char] # 直接将当前node的next中以remove_char为键的 键值对 删除
string_index -= 1 # 同步操作,维护一下string_index,准备删除下一个字符
self._size -= 1 # 最后删完了别忘记维护一下self._size
def printTrie(self):
"""打印Trie,为了debug用的。凑合看吧/(ㄒoㄒ)/~~前缀打印不出来--救我~"""
def _printTrie(node):
if not len(node.next): # 递归到底的情况,下面没Node了
print('None')
return
for keys in node.next.keys(): # 对当前node的下面的每个character
print(keys, end='->') # 打印character
_printTrie(node.next[keys]) # 依次对下面的每个node都调用_printTrie方法来递归打印
_printTrie(self._root)
四、测试
# -*- coding: utf-8 -*-
import sys
sys.path.append('/home/tony/Code/data_structure')
from dict_tree import trie
test = trie.Trie() # 非递归测试
test_re = trie.Trie() # 递归测试
record = ['你好', 'hello', 'こんにちは', 'pan', 'panda', '我是大哥大666']
print('初始化是否为空?', test.isEmpty())
print('此时的size:', test.getSize())
print('=' * 20)
print('测试非递归版本的成员函数:')
print('将record中的字符串全部添加进test中:')
for elem in record:
test.add(elem)
print('打印:')
test.printTrie()
print('判断record中的元素是否都已经存在于test中:')
for elem in record[::-1]:
flag = test.contains(elem)
if flag:
print('"%s" 存在于 test 中。' % elem)
print('此时test的size:', test.getSize())
print('"hel"是否是test的前缀?', test.isPrefix('hel'))
print('='*20)
print('仅针对test进行删除操作,test_re类似就不处理了')
print('删除"pan"并打印:')
test.remove('pan')
test.printTrie()
print('删除"我是大哥大666"并打印:')
test.remove('我是大哥大666')
test.printTrie()
print('此时test的容量:', test.getSize())
print('=' * 20)
print('测试递归版本的成员函数:')
print('将record中的字符串全部添加进test_re中:')
for elem in record:
test_re.add_RE(test_re._root, elem, 0)
print('打印:')
test.printTrie()
print('判断record中的元素是否都已经存在于test_re中:')
for elem in record[::-1]:
flag = test_re.contains_RE(test_re._root, elem, 0)
if flag:
print('"%s" 存在于 test_re 中。' % elem)
print('此时test_re的size:', test_re.getSize())
print('"こんに"是否是test_re的前缀?', test_re.isPrefix('こんに'))
五、输出
初始化是否为空? True
此时的size: 0
====================
测试非递归版本的成员函数:
将record中的字符串全部添加进test中:
打印:
你->好->None
h->e->l->l->o->None
こ->ん->に->ち->は->None
p->a->n->d->a->None
我->是->大->哥->大->6->6->6->None
判断record中的元素是否都已经存在于test中:
"我是大哥大666" 存在于 test 中。
"panda" 存在于 test 中。
"pan" 存在于 test 中。
"こんにちは" 存在于 test 中。
"hello" 存在于 test 中。
"你好" 存在于 test 中。
此时test的size: 6
"hel"是否是test的前缀? True
====================
仅针对test进行删除操作,test_re类似就不处理了
删除"pan"并打印:
你->好->None
h->e->l->l->o->None
こ->ん->に->ち->は->None
p->a->n->d->a->None
我->是->大->哥->大->6->6->6->None
删除"我是大哥大666"并打印:
你->好->None
h->e->l->l->o->None
こ->ん->に->ち->は->None
p->a->n->d->a->None
此时test的容量: 4
====================
测试递归版本的成员函数:
将record中的字符串全部添加进test_re中:
打印:
你->好->None
h->e->l->l->o->None
こ->ん->に->ち->は->None
p->a->n->d->a->None
判断record中的元素是否都已经存在于test_re中:
"我是大哥大666" 存在于 test_re 中。
"panda" 存在于 test_re 中。
"pan" 存在于 test_re 中。
"こんにちは" 存在于 test_re 中。
"hello" 存在于 test_re 中。
"你好" 存在于 test_re 中。
此时test_re的size: 6
"こんに"是否是test_re的前缀? True
六、习题
Leetcode 208:
Implement a trie with insert, search, and startsWith methods.
Example:
Trie trie = new Trie();
trie.insert(“apple”);
trie.search(“apple”); // returns true
trie.search(“app”); // returns false
trie.startsWith(“app”); // returns true
trie.insert(“app”);
trie.search(“app”); // returns true
Note:
You may assume that all inputs are consist of lowercase letters a-z.
All inputs are guaranteed to be non-empty strings.
# Your Code 216ms
# 这题几乎就是我们以前实现的一些典型操作嘛。。非常的简单,很好的练手题。
# -*- coding: utf-8 -*-
# Author: Annihilation7
# Data: 2018-12-23 15:39
# Python version: 3.6
class Node:
# 肯定是要新建一个node类的!
def __init__(self, is_Word=False):
self.is_word = is_Word
self.next = dict()
class Trie:
def __init__(self):
"""
Initialize your data structure here.
"""
self._root = Node()
self._size = 0
def insert(self, word):
"""
Inserts a word into the trie.
:type word: str
:rtype: void
"""
cur = self._root
for character in word:
flag = cur.next.get(character, None)
if flag is None:
cur.next[character] = Node()
cur = cur.next[character]
if not cur.is_word:
cur.is_word = True
self._size += 1
def search(self, word):
"""
Returns if the word is in the trie.
:type word: str
:rtype: bool
"""
cur = self._root
for character in word:
cur = cur.next.get(character, None)
if cur is None:
return False
if cur.is_word:
return True
return False
def startsWith(self, prefix):
"""
Returns if there is any word in the trie that starts with the given prefix.
:type prefix: str
:rtype: bool
"""
def _startWith_re(node, prefix, index):
# 这里我用递归来写的,练习一下递归的写法。
if index == len(prefix):
return True
ret = node.next.get(prefix[index], None)
if ret is None:
return False
return _startWith_re(node.next[prefix[index]], prefix, index + 1)
return _startWith_re(self._root, prefix, 0)
# Your Trie object will be instantiated and called as such:
# obj = Trie()
# obj.insert(word)
# param_2 = obj.search(word)
# param_3 = obj.startsWith(prefix)
Letcode 211:
Design a data structure that supports the following two operations:
void addWord(word)
bool search(word)
search(word) can search a literal word or a regular expression string containing only letters a-z or … A . means it can represent any one letter.
Example:
addWord(“bad”)
addWord(“dad”)
addWord(“mad”)
search(“pad”) -> false
search(“bad”) -> true
search(".ad") -> true
search(“b…”) -> true
Note:
You may assume that all words are consist of lowercase letters a-z.
# Your code 504ms
# 题意简介名了,多了一个通配符'.',能够匹配任意一个字符,所以遇到这个循环遍历一遍当前node的next的所有node即可。
class Node:
def __init__(self, isWord=False):
self.is_Word = isWord
self.next = dict()
class WordDictionary:
def __init__(self):
"""
Initialize your data structure here.
"""
self._root = Node()
self._size = 0
def addWord(self, word):
"""
Adds a word into the data structure.
:type word: str
:rtype: void
"""
# 这里用递归写的,和前面的函数一样
def _addWord_re(node, word, index):
if index == len(word):
if not node.is_Word:
node.is_Word = True
self._size += 1
return
flag = node.next.get(word[index], None)
if flag is None:
node.next[word[index]] = Node()
_addWord_re(node.next[word[index]], word, index + 1)
_addWord_re(self._root, word, 0)
def search(self, word):
"""
Returns if the word is in the data structure. A word could contain the dot character '.' to represent any one letter.
:type word: str
:rtype: bool
"""
def _search_re(node, word, index):
"""
递归版本的search,需要考虑通配符'.',其实非常简单,遇到'.'就把所有的下一个有效节点全部递归的search一下就好了。
"""
if index == len(word):
return node.is_Word
if word[index] != '.': # 不是'.'的情况,和以前一样的,很简单
flag = node.next.get(word[index], None)
if flag is None:
return False
return _search_re(node.next[word[index]], word, index + 1)
else: # 此时遇到'.',表明需要匹配当前next节点中所有的有效节点,循环遍历一下即可,和打印Trie的操作思想是一致的
for tmp_node in node.next.values(): # 遍历所有next中的有效节点
if _search_re(tmp_node, word, index + 1):
return True # 找到了就返回Ture
return False # 转了一圈还没匹配到,那就返回False
# 千万不能写成 return _research_re(tmp_node, word, index + 1)
# 因为我们的目标是要匹配到字符串,这么写在循环中如果出现有一次没匹配到就返回False了,此时剩余的字符我们还没
# 判断呢!
return _search_re(self._root, word, 0)
# Your WordDictionary object will be instantiated and called as such:
# obj = WordDictionary()
# obj.addWord(word)
# param_2 = obj.search(word)
Leetcode 677:
Implement a MapSum class with insert, and sum methods.
For the method insert, you’ll be given a pair of (string, integer). The string represents the key and the integer represents the value. If the key already existed, then the original key-value pair will be overridden to the new one.
For the method sum, you’ll be given a string representing the prefix, and you need to return the sum of all the pairs’ value whose key starts with the prefix.
Example 1:
Input: insert(“apple”, 3), Output: Null
Input: sum(“ap”), Output: 3
Input: insert(“app”, 2), Output: Null
Input: sum(“ap”), Output: 5
# Your code 44ms
# 用Trie改写成一个字典,insert方法很简单,和以前一样。但是sum方法没见过,求的是以输入的字符串为前缀的所有字符串的和。
class Node:
def __init__(self, value=0):
self.value = value # 代表字典的value值,默认是0。比如加入元素"("xyz", 3)",那么x, y的value都是0,只有z的value是3。
self.next = dict()
class MapSum:
def __init__(self):
"""
Initialize your data structure here.
"""
self._root = Node()
self._size = 0
def insert(self, key, val):
"""
:type key: str
:type val: int
:rtype: void
"""
cur = self._root
for key_character in key:
flag = cur.next.get(key_character, None)
if flag is None:
cur.next[key_character] = Node() # 默认的value都是0哦~
cur = cur.next[key_character]
cur.value = val # 最后一个字符赋予value值为val
def sum(self, prefix):
"""
想都不用想,求和肯定是递归来求的。
:type prefix: str
:rtype: int
"""
def _sum_re(node): # 求和的递归函数,输入一个Node,求以该node为根的Trie树满足相应条件的和
if len(node.next) == 0: # 递归到底的情况
return node.value
res = node.value # 获取当前node的value
for tmp_node in node.next.values(): # 对后面的每一个node
res += _sum_re(tmp_node) # 都加上后面的node的value,即使是中间的字符也没问题,因为他们的value为0
return res
cur = self._root # 要先定位到prefix的最后一个字符哦,否则何来的以prefix为前缀求和呢?
for pre_character in prefix:
flag = cur.next.get(pre_character, None)
if flag is None:
return 0
cur = cur.next[pre_character]
return _sum_re(cur) # 调用求和递归函数。
# Your MapSum object will be instantiated and called as such:
# obj = MapSum()
# obj.insert(key,val)
# param_2 = obj.sum(prefix)
七、总结
- 首先托更了很长时间,对不起小伙伴了,当时都想放弃了,原因就是我太忙(lan)了,当时想自己会就行了更博客也没什么意义/(ㄒoㄒ)/~~,直到有一个小伙伴在“线段树”那节评论我为什么不更新了,让我看到了还有人在等我写,好感动,就是再忙也要坚持写下去!
- Trie添加、查询操作的时间复杂度与当前元素总数无关,只正比于当前字符串的长度!
- Trie是一个非常非常重要的数据结构,要好好消化、理解,多多debug。
- Trie的最大的问题——空间!改进就是“压缩字典树”,相应的维护成本也变高了,有兴趣的小伙伴可以实现一下。/(ㄒoㄒ)/~~另一个改进就是“三分搜索树”。
若有还可以改进、优化的地方,还请小伙伴们批评指正!
