pythonAIC准则下线性回归实现及模型检验案例分析

#coding=utf/8
#time:2019/8/11
#function:线性回归
#author：Karen
import pandas as pd
import numpy as np
import statsmodels.api as sm
import matplotlib.pyplot as plt
from sklearn import preprocessing
import statsmodels.formula.api as smf
from sklearn.model_selection import train_test_split
from sklearn.metrics import mean_squared_error
import math
#解决负号显示问题
from matplotlib import font_manager as fm


#数据预处理及数据探索
def get_data():
    f=open('北京高端酒店价格.csv',encoding='utf/8')
    data=pd.read_csv(f,encoding='utf/8')
    st=''
    for i in data['地区'].unique():
        st=st+'，'+i
    print(st)
    print(data['位置评分'].describe())
    data['装修时间']=data['装修时间'].apply(lambda x: '新装修' if x>2015 else '旧装修')
    # tim=data['装修时间'].unique()
    # typ=data['房间类型'].unique()
    # location=data['地区'].unique()
    #哑变量
    df1=pd.get_dummies(data['房间类型'])
    df2=pd.get_dummies(data['地区'])
    df3=pd.get_dummies(data['装修时间'])
    data=pd.concat([data,df1,df2,df3],axis=1)
    data.drop(['房间类型','地区'],inplace=True,axis=1)
    #改变索引
    price=data['房价']
    data.drop('房价',inplace=True,axis=1)
    data.insert(0,'房价',price)
    # data['新装修']=data.loc[22]
    print(data.head())
    data.drop(['酒店名称','经度','纬度','地址','其他城区','标准间','装修时间','旧装修'],inplace=True,axis=1)
    data['对数房价']=data['房价'].apply(lambda x:math.log(x))
    print(data.head())
    data=data.round(1)
    #数据标准化
    a=data.columns.values.tolist()
    X_scaled = preprocessing.scale(data)
    data=pd.DataFrame(X_scaled)
    data.columns=a
    data.to_csv('北京酒店价格anlysis.csv')
    return data

#模型建立
def model_extablish(formula):
    f=open('北京酒店价格anlysis.csv',encoding='utf/8')
    data=pd.read_csv(f,encoding='utf/8')
#切分数据集
    Train, Test = train_test_split(data, train_size=0.8, random_state=1234)
    fit = smf.ols('对数房价~卫生评分+服务评分+设施评分+位置评分+评价数+新装修+公司+出行住宿+校园生活+豪华套间+商务间+海淀区+东城区+朝阳区', data=Train).fit()
    print(fit.summary())
#计算RMSE
    pred = fit.predict(exog=Test)
    RMSE = np.sqrt(mean_squared_error(Test['对数房价'], pred))
    print('第一个模型的预测效果：RMES=%.4f\n' % RMSE)

# 绘制真实值与预测值的关系
# 真实值与预测值的关系# 设置绘图风格
# plt.style.use('ggplot')
# 设置中文编码和负号的正常显示
plt.rc("font", family="SimHei", size="9")

# 散点图
plt.scatter(Test['对数房价'], pred, label='观测点')
# 回归线
plt.plot([Test['对数房价'].min(), Test['对数房价'].max()], [pred.min(), pred.max()], 'r--', lw=2, label='拟合线')

结果展示：

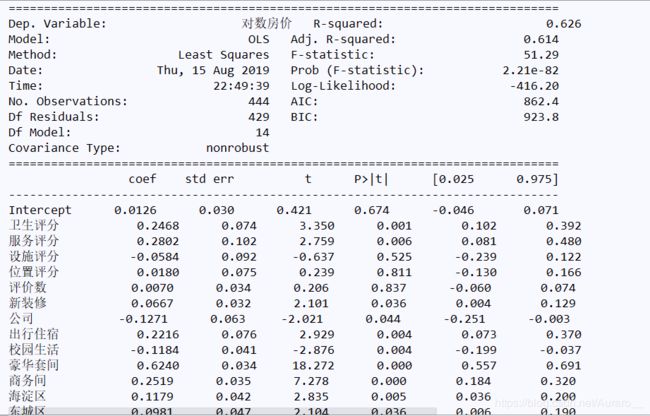
查看F值，小于0.01，通过F检验，说明至少有一个变量显著，查看各变量P值，选定显著性水平，进行比较，R方0.645，大于0.5，。

 # 添加轴标签和标题
    plt.title('真实值VS.预测值')
    plt.xlabel('真实值')
    plt.ylabel('预测值'

)

# 去除图边框的顶部刻度和右边刻度
plt.tick_params(top='off', right='off')
# 添加图例
plt.legend(loc='upper left')
# 图形展现
plt.show()

采用AIC准则对变量进行筛选

#定义向前逐步回归函数
def forward_select(target='对数房价'):
    #读取文件
    f = open('北京酒店价格anlysis.csv', encoding='utf/8')
    data = pd.read_csv(f, encoding='utf/8')
    data.drop('房价',inplace=True,axis=1)
    Train, Test = train_test_split(data, train_size=0.8, random_state=1234)
    variate=set(data.columns)  #将字段名转换成字典类型
    variate.remove(target)  #去掉因变量的字段名
    selected=[]
    current_score,best_new_score=float('inf'),float('inf')  #目前的分数和最好分数初始值都为无穷大（因为AIC越小越好）
    #循环筛选变量
    while variate:
        aic_with_variate=[]
        for candidate in variate:  #逐个遍历自变量
            formula="{}~{}".format(target,"+".join(selected+[candidate]))  #将自变量名连接起来
            aic=smf.ols(formula=formula,data=Train).fit().aic  #利用ols训练模型得出aic值
            aic_with_variate.append((aic,candidate))  #将第每一次的aic值放进空列表
        aic_with_variate.sort(reverse=True)  #降序排序aic值
        best_new_score,best_candidate=aic_with_variate.pop()  #最好的aic值等于删除列表的最后一个值，以及最好的自变量等于列表最后一个自变量
        if current_score>best_new_score:  #如果目前的aic值大于最好的aic值
            variate.remove(best_candidate)  #移除加进来的变量名，即第二次循环时，不考虑此自变量了
            selected.append(best_candidate)  #将此自变量作为加进模型中的自变量
            current_score=best_new_score  #最新的分数等于最好的分数
            print("aic is {},continuing!".format(current_score))  #输出最小的aic值
        else:
            print("for selection over!")
            break
    formula="{}~{}".format(target,"+".join(selected))  #最终的模型式子
    print("final formula is {}".format(formula))
    return formula

对模型进行检验

def test_model(formula):
    f = open('北京酒店价格anlysis.csv', encoding='utf/8')
    data = pd.read_csv(f, encoding='utf/8')
    Train, Test = train_test_split(data, train_size=0.8, random_state=1234)
    fit = smf.ols(formula,Test).fit()
results = pd.DataFrame({
                        'resids': fit.resid,  # 残差
                        'std_resids': fit.resid_pearson,  # 方差标准化的残差
                        'fitted': fit.predict() }) # y预测值

                        # ====== 图示法完成方差齐性的判断 ======
# 标准化残差与预测值之间的散点图
plt.scatter(fit.predict(), results['std_resids'])
plt.xlabel('预测值')
plt.ylabel('标准化残差')
# 添加水平参考线
plt.axhline(y=0, color='r', linewidth=2)
plt.show()
# ====== 统计法完成方差齐性的判断 ======
#查看第二项P值
# White's Test
print(sm.stats.diagnostic.het_white(fit.resid, exog=fit.model.exog))
# Breusch-Pagan
print(sm.stats.diagnostic.het_breuschpagan(fit.resid, exog_het=fit.model.exog))
# ======残差非正态性和Q-Q图 ======
qqplot = sm.qqplot(results['std_resids'], line='s')
plt.xlabel('Theoretical quantiles')
plt.ylabel('Sample quantiles')
plt.title('Normal Q-Q')
plt.show(qqplot)

# ======强影响点和COOK距离 ======
proptease = fm.FontProperties()
proptease.set_size('xx-small')
fig, ax = plt.subplots(figsize=(19.2, 14.4))
fig = sm.graphics.influence_plot(fit, ax=ax, criterion='Cooks',size=0.2,fontproperties=proptease)
plt.xlabel('Obs.number')
plt.ylabel("Cook's distance")
plt.title("Cook's distance")
plt.grid()
plt.show()
plt.close()

# ======在同一画布显示 ======
fontdict = {'family': 'Times New Roman',
         'weight': 'normal',
         'size': 9,
         }
fig = plt.figure(figsize=(20, 20), dpi=100)

ax1 = fig.add_subplot(2, 2, 1)
ax1.plot(results['fitted'], results['resids'], 'o')
ax1.set_xlabel('Fitted values',fontdict=fontdict)
ax1.set_ylabel('Residuals',fontdict=fontdict)
ax1.set_title('Residuals vs Fitted',fontdict=fontdict)
ax1.axhline(y=0, color='r', linewidth=2)

ax2 = fig.add_subplot(2, 2, 2)
sm.qqplot(results['std_resids'], line='s', ax=ax2)
ax2.set_xlabel('Theoretical quantiles',fontdict=fontdict)
ax2.set_ylabel('Sample quantiles',fontdict=fontdict)
ax2.set_title('Normal Q-Q',fontdict=fontdict)

ax3 = fig.add_subplot(2, 2, 3)
ax3.plot(results['fitted'], abs(results['std_resids']) ** .5, 'o')
ax3.set_xlabel('Fitted values',fontdict=fontdict)
ax3.set_ylabel('Sqrt(|standardized residuals|)',fontdict=fontdict)
ax3.set_title('Scale-Location',fontdict=fontdict)
ax3.axhline(y=0.8, color='r', linewidth=2)

ax4 = fig.add_subplot(2, 2, 4)
sm.graphics.influence_plot(fit, criterion='Cooks', size=0.2, ax=ax4)
ax4.set_xlabel('Obs.number',fontdict=fontdict)
ax4.set_ylabel("Cook's distance",fontdict=fontdict)
ax4.set_title("Cook's distance",fontdict=fontdict)
plt.show()

结果展示：



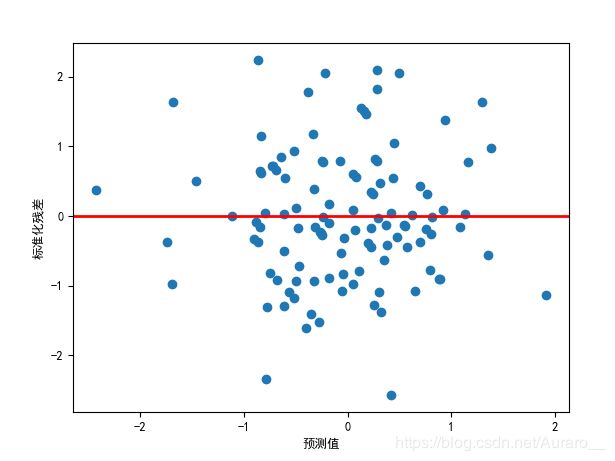
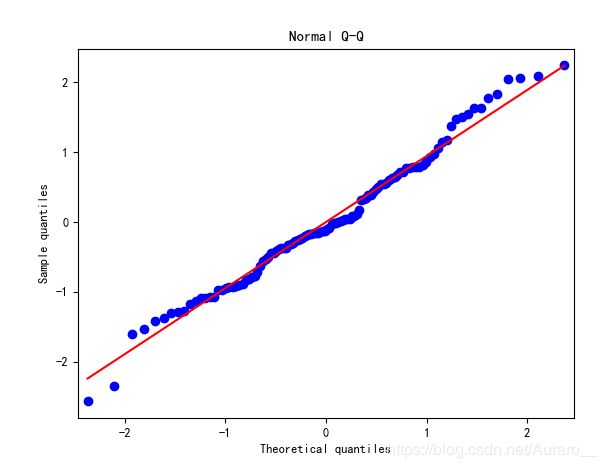
残差基本服从正态分布，存在部分强影响点，具有改进空间

if __name__ == '__main__':
	get_data()
    test_model(forward_select())

因为是直接调用sm库内画cook距离，所以在最后一张画布的时候虽然整体调整了字体大小，但是内部字体大小还是没有调节成功，希望可以有大佬指点一下，感谢！