排队论模型及MATLAB实现

1. 按

生活中需要排队的地方很多，本模型用于分析和仿真现实生活中的排队现象。
排队论发源于上世纪初。当时美国贝尔电话公司发明了自动电话，以适应日益繁忙的工商业电话通讯需要。这个新发明带来了一个新问题，即通话线路与电话用户呼叫的数量关系应如何妥善解决，这个问题久久未能解决。
1909年，丹麦的哥本哈根电话公司A.K.埃尔浪(Erlang)在热力学统计平衡概念的启发下解决了这个问题。1917 年，爱尔朗发表了他的著名的文章—“自动电话交换中的概率理 论的几个问题的解决”。排队论已广泛应用于解决军事、运输、维修、生产、服务、库 存、医疗卫生、教育、水利灌溉之类的排队系统的问题，显示了强大的生命力。

2. 排队现象

排队是在日常生活中经常遇到的现象，如顾客到商店购买物品、病人到医院看病常 常要排队。此时要求服务的数量超过服务机构（服务台、服务员等）的容量。也就是说， 到达的顾客不能立即得到服务，因而出现了排队现象。这种现象不仅在个人日常生活中 出现，电话局的占线问题，车站、码头等交通枢纽的车船堵塞和疏导，故障机器的停机 待修，水库的存贮调节等都是有形或无形的排队现象。由于顾客到达和服务时间的随机性。可以说排队现象几乎是不可避免的。

到达顾客	服务内容	服务机构
病人	诊断/手术	医生/手术台
进港的货船	装货/卸货	码头泊位
到港的飞机	降落	机场跑道
电话拨号	通话	交换台
故障机器	修理	修理技工
修理技工	领取修配零件	仓库管理员
上游河水	入库	水闸管理员

3. 模型介绍

（1）由于顾客到达和服务时间的随机性，
现实中的排队现象几乎不可避免；
（2）排队过程，通常是一个随机过程，
排队论又称“随机服务系统理论”；

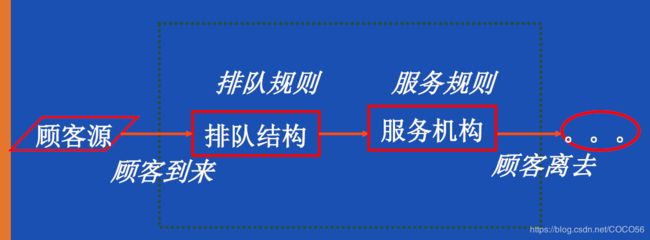
3.1. 排队服务过程

3.2. 排队系统的要素

（1）顾客输入过程；
（2）排队结构与排队规则；
（3）服务机构与服务规则；

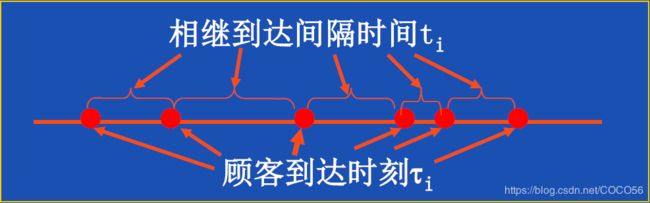
3.3. 顾客输入过程

顾客源(总体)：有限/无限;
顾客到达方式：逐个/逐批;(仅研究逐个情形)
顾客到达间隔：随机型/确定型;
顾客前后到达是否独立：相互独立/相互关联；
输入过程是否平稳：平稳/非平稳；(仅研究平稳性)

3.4. 排队结构与排队规则

顾客排队方式：等待制/即时制(损失制);
排队系统容量：有限制/无限制;
排队队列数目: 单列/多列;
是否中途退出: 允许/禁止;
是否列间转移: 允许/禁止;
(仅研究禁止退出和转移的情形)

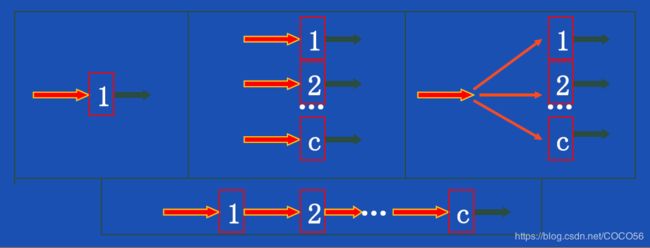
3.5. 服务机构与服务规则

服务台(员)数目;单个/多个;
服务台(员)排列形式;并列/串列/混合;
服务台(员)服务方式;逐个/逐批;(研究逐个情形)
服务时间分布;随机型/确定型;
服务时间分布是否平稳:平稳/非平稳;(研究平稳情形)

3.6. 服务台(员)为顾客服务的顺序

a)先到先服务(FCFS);
b)后到先服务(LCFS);
c)随机服务;
d)优先服务;

3.7. 到达间隔和服务时间典型分布

（1）泊松分布M ；
（2）负指数分布M ；
（3）k阶爱尔朗分布Ek；
（4）确定型分布D；
（5）一般服务时间分布G；

3.8. 排队模型示例

——M/M/1，M/D/1，M/ Ek /1；
——M/M/c，M/M/c/∞/m，
——M/M/c/N/∞，…

3.9. 系统运行状态参数

• 系统状态N(t)：指排队系统在时刻t时的全部顾客数N(t)，包括“排队顾客数”和“正被服务顾客数”；
• 系统状态概率：
  1. 瞬态概率$P_n(t)$：表示时刻t系统状态N(t)=n 的概率;
  2. 稳态概率$P_n$：
     $P_n={\lim }_{t\to \infty }{P}_n(t)$
     一般排队系统运行了一定长的时间后，系统状态的概率分布不再随时间t变化，即初始时刻（t=0）系统状态的概率分布 ($P_n(0)$, n>>0）的影响将消失。

3.10. 系统运行指标参数

用于评价排队系统的优劣。

1. 队长与排队长
   (1)队长: 系统中的顾客数(n)期望值记为$L_s$；
   (2)排队长: 系统中排队等待服务的顾客数;
   期望值记为$L_q$
2. 逗留时间与等待时间
   (1)逗留时间：指一个顾客在系统中的全部停留时间；期望值，记为$W_{\mathrm{s}}$
   (2)等待时间:指一个顾客在系统中的排队等待时间；期望值，记为$W_{\mathrm{q}}$
   $W_{\mathrm{s}}$= $W_{\mathrm{q}}$ + E[服务时间]
3. 其他相关指标
   (1)忙期: 指从顾客到达空闲服务机构起到服务机构再次空闲的时间长度；
   (2)忙期服务量：指一个忙期内系统平均完成服务的顾客数；
   (3)损失率: 指顾客到达排队系统，未接受服务而离去的概率；
   (4)服务强度：ρ= λ/sμ；

3.11. 顾客到达时间间隔分布

泊松流与泊松分布

• 如果顾客到达满足如下条件,则称为泊松流
  (1) 在不相互重叠的时间区间内，到达顾客数相互独立(无后效性).
  (2) 对于充分小的时间间隔[t, t+∆t]内，到达1个顾客的概率与t无关，仅与时间间隔成正比 (平稳性)：$P_1(t,t+\Delta t)=\lambda \Delta t+o(\Delta t)$
  (3) 对于充分小的时间间隔[t, t+∆t]，2个及以上顾客到达的概率可忽略不计 (普通性)。
• 泊松流到达间隔服从负指数分布
  若顾客到达间隔T的概率密度为$f_T(t)=\{\begin{array}{ll}\lambda e^{-\lambda t},& t\ge 0\\ 0& ,t<0\end{array}$则称T服从负指数分布，分布函数为：$F_T(t)=\{\begin{array}{ll}1-\lambda e^{-\lambda t},& t\ge 0\\ 0& ,t<0\end{array}$
  若顾客流是泊松流时，顾客到达的时间间隔服从上述负指数分布
  $\mathrm{E}[\mathrm{T}]=1/\lambda ;\mathrm{Var}[\mathrm{T}]=1/{\lambda }^2;\sigma [\mathrm{T}]=1/\lambda$

3.12. 顾客服务时间分布

负指数分布

• 对一个顾客的服务时间${\mathbf{T}}_{\mathbf{s}}$，等价于相邻两个顾客离开排队系统的时间间隔。若${\mathbf{T}}_{\mathbf{s}}$服从负指数分布，其概率密度和分布函数分别为：
  $$f_{T_s}(t)=\{\begin{array}{ll}\mu e^{-\mu t}& ,t\ge 0\\ 0& ,t<0\end{array}{F}_{T_s}(t)=\{\begin{array}{ll}1-\mu e^{-\mu t}& ,t\ge 0\\ 0& ,t<0\end{array}$$
  则$\mathbf{E}[{\mathbf{T}}_{\mathbf{s}}]=1/\mu ;\mathbf{V}\mathbf{a}\mathbf{r}[{\mathbf{T}}_{\mathbf{s}}]=1/\mu 2;\sigma [{\mathbf{T}}_{\mathbf{s}}]=1/\mu$
• $\mathbf{E}[{\mathbf{T}}_{\mathbf{s}}]=1/\mu$：每个顾客的平均(期望)服务时间；
  μ:单位时间服务的顾客数，平均(期望)服务率；

3.13. 单服务台负指数分布M/M/1排队系统

• 模型的条件是：
  1、输入过程――顾客源是无限的，顾客到达完全是随机的，单个到来，到达过程服从普阿松分布，且是平稳的；
  2、排队规则――单队，且队长没有限制，先到先服务；
  3、服务机构――单服务台，服务时间的长短是随机的，服从相同的指数分布。

这里的M/M/1如未设置N（系统空间，即等候区的最大容纳量）则指M/M/1/∞
单服务台等待制模型 M/M/1/∞ 是指：顾客的相继到达时间服从参数为λ的负指数分布，服务台个数为1，服务时间V服从参数为 μ的负指数分布，系统空间无限， 允许无限排队，这是一类最简单的排队系统。

• 对于M／M／1模型有如下公式：
  $$\begin{array}{ll}{P}_0=1-\rho & P_n={\rho }^n(1-\rho )\\ L_s=\frac{\lambda }{\mu -\lambda }=\frac{\rho }{1-\rho }& L_q=\frac{{\lambda }^2}{\mu (\mu -\lambda )}=\frac{{\rho }^2}{1-\rho }=L_s\rho \\ W_s=\frac{1}{\mu -\lambda }& W_q=\frac{\lambda }{\mu (\mu -\lambda )}=W_s\rho \\ P(N>k)={\rho }^{k+1}(N表示系统中的顾客数)& \end{array}$$

3.14. M/M/S模型

此模型与M/M/1模型不同之处在于有S个服务台，各服务台的工作相互独立，服务率相等，如果顾客到达时，S个服务台都忙着，则排成一队等待，先到先服务的单队模型。
整个系统的平均服务率为：$s\mu ,{\rho }^{\ast }=\lambda /s\mu ,({\rho }^{\ast }<1)$，为该系统的服务强度。

• 状态概率
  $$\begin{array}{l}{P}_0={\left[{\sum }_{k=0}^{S-1}\frac{1}{k!}{\left(\frac{\lambda }{\mu }\right)}^k+\frac{1}{s!}\frac{1}{1-{\rho }^{\ast }}{\left(\frac{\lambda }{\mu }\right)}^S\right]}^{-1}\\ P_n=\{\begin{array}{ll}\frac{1}{n!}{\left(\frac{\lambda }{\mu }\right)}^n{P}_0& O<n\le S\\ \frac{1}{S!S^{n-s}}{\left(\frac{\lambda }{\mu }\right)}^n{P}_0& n\ge S\end{array}\end{array}$$
• 主要运行指标
  $$\begin{array}{ll}{L}_{\mathrm{q}}=\frac{{\left(\mathrm{S}{\rho }^{\ast }\right)}^{\mathrm{s}}{\rho }^{\ast }}{S!{\left(1-{\rho }^{\ast }\right)}^2}{P}_0& L_s=L_q+s{\rho }^{\ast }\\ W_{\mathrm{q}}=\frac{L_{\mathrm{q}}}{\lambda }& W_s=\frac{L}{\lambda }=W_q+\frac{1}{\mu }\end{array}$$
• 系统状态N ≥S的概率
  $$P(N\ge \mathrm{k})=\sum _{\mathrm{n}=\mathrm{k}}^{\infty }{P}_{\mathrm{n}}=\frac{{\rho }^{\mathrm{k}}}{\mathrm{k}!\left(1-{\rho }^{\ast }\right)}{P}_0$$

4. 模型举例

4.1. 例1(MM1)

某医院急诊室同时只能诊治一个病人，诊治时间服从指数分布，每个病人平均需要15分钟。病人按泊松分布到达，平均每小时到达3人。试对此排队队系统进行分析。
解 对此排队队系统分析如下：

1. 先确定参数值：这是单服务台系统，有：
   $$\lambda =3人/h,\mu =\frac{60}{15}人/h=4人/h$$
   故服务强度为：
   $$\rho =\frac{\lambda }{\mu }=\frac{3}{4}=0.75$$
   计算稳态概率：
   $$P_0=1-\rho =1-0.75=0.25$$
   这就是急诊室空闲的概率，也是病人不必等待立即就能就诊的概率。而病人需要等待的概率则为：
   $$\rho =1-P_0=0.75$$
   这也是急诊室繁忙的概率。
2. 计算系统主要工作指标。
   急诊室内外的病人平均数：
   $$L_s=\frac{\lambda }{\mu -\lambda }=\frac{3}{4-3}人=3人$$
   急诊室外排队等待的病人平均数：
   $$L_q=L_s\rho =3\times 0.75人a=2.25人$$
   病人在急诊室内外平均逗留时间：
   $$W_s=\frac{1}{\mu -\lambda }=\frac{1}{4-3}\mathbf{h}=1\mathbf{h}=60\min$$
   病人平均等候时间：
   $$W_q=W_s\rho =1\times 0.75h=0.75h=45\mathrm{m}\mathrm{i}\mathrm{n}$$

4.2. 例2(MMS)

承接例1，假设医院增强急诊室的服务能力，使其同时能诊治两个病人，且平均服务率相同，试分析该系统工作情况。
解 这相当于增加了一个服务台，故有：S=2,λ=3人/h，μ=4人/h
$$\begin{array}{l}\rho =\frac{\lambda }{\mu }=0.75,{\rho }^{\ast }=\frac{\lambda }{\mathrm{S}\mu }=\frac{3}{2\times 4}=0.375\\ P_o={\left[1+0.75+\frac{(0.75{)}^2}{2!(1-0.375)}\right]}^{-1}=\frac{5}{11}=0.45\\ L_q=\frac{(0.75{)}^2\times 0.375}{2!(1-0.375{)}^2}\times \frac{5}{11}=0.27\times \frac{5}{11}人\approx 0.12人\\ L_s=L_q+\rho =(0.12+0.75)人=0.87人\\ W_s=\frac{L_s}{\lambda }=\frac{0.87}{3}=0.29h=17.4\mathrm{m}\mathrm{i}\mathrm{n}\\ W_q=\frac{L_q}{\lambda }=\frac{0.12}{3}0.04h=2.4\mathrm{m}\mathrm{i}\mathrm{n}\end{array}$$
病人必须等候的概率,即系统状态N≥2的概率：
$$P(N\ge 2)=\frac{(0.75{)}^2}{2!(1-0.375)}\times \frac{5}{11}\approx 0.20$$

4.3. 例3

某医院挂号室有三个窗口，就诊者的到达服从泊松分布，平均到达率为每分钟0.9人，挂号员服务时间服从指数分布，平均服务率每分钟0.4人，现假设就诊者到达后排成一队，依次向空闲的窗口挂号，显然系统的容量和顾客源是不限的，属于M/M/S型的排队服务模型。求：该系统的运行指标$P_0,L_q,L,W_q,W,P(N\ge 3)$
解
$$S=3,\rho =\frac{\lambda }{\mu }=\frac{0.9}{0.4}=2.25,{\rho }^{\ast }=\frac{\lambda }{S\mu }=\frac{2.25}{3}=\frac{3}{4}<1$$

1. 整个挂号间空闲的概率：
   $$P_0={\left[\frac{(2.25{)}^0}{0!}+\frac{(2.25{)}^1}{1!}+\frac{(2.25{)}^2}{2!}+\frac{(2.25{)}^3}{3!}\frac{1}{1-2.25/3}\right]}^{-1}=0.0748$$
2. 等待挂号的平均人数或称队列长
   $$L_q=\frac{(2.25{)}^3\cdot 3/4}{3!}\times 0.0748=1.7人$$
3. 挂号间平均逗留人数或称队长
   $$L=L_q+\frac{\lambda }{\mu }=1.7+2.25=3.95人$$
4. 等候挂号的平均时间
   $$W_q=\frac{1.7}{0.9}=1.89分钟$$
5. 在挂号间平均逗留时间
   $$W=1.89+\frac{1}{0.4}=4.39分钟$$
6. 就诊者到达后必须等待（即系统中就诊者不少于3人或各挂号员都没有空闲）的概率
   $$P(N\ge 3)=\frac{(2.25{)}^3}{3!\times 1/4}\times 0.0748=0.57$$

5. matlab实现

5.1. 无绘图版

• 源码

  s=2; %服务台的个数
  mu=4; %单位时间内能服务的顾客数
  lambda=3; %单位时间内到达的顾客数
  
  ro=lambda/mu;
  ros=ro/s;
  sum1=0;
  
  for i=0:(s-1) sum1=sum1+ro.^i/factorial(i); end
  
  sum2=ro.^s/factorial(s)/(1-ros);
  
  p0=1/(sum1+sum2);
  p=ro.^s.*p0/factorial(s)/(1-ros);
  Lq=p.*ros/(1-ros);
  L=Lq+ro;
  W=L/lambda;
  Wq=Lq/lambda;
  fprintf('排队等待的平均人数为%5.2f人\n',Lq)
  fprintf('系统内的平均人数为%5.2f人\n',L)
  fprintf('平均逗留时间为%5.2f分钟\n',W*60)
  fprintf('平均等待时间为%5.2f分种\n',Wq*60)
  

• 结果
  排队等待的平均人数为 0.12人
  系统内的平均人数为 0.87人
  平均逗留时间为17.45分钟
  平均等待时间为 2.45分种
  

5.2. 绘图版

5.2.1. 测试一

• 源码

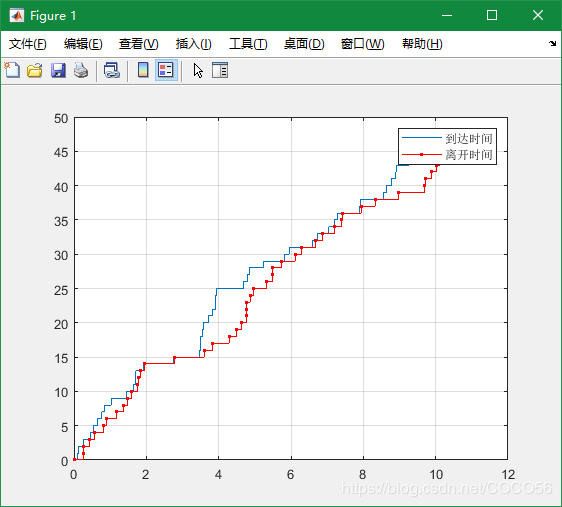
  clear 
  clc 
  %***************************************** 
  %初始化顾客源 
  %***************************************** 
  %总仿真时间 
  Total_time = 10; 
  %队列最大长度 
  N=10000000000; 
  %到达率与服务率 
  lambda=10, mu=6;
  %平均到达时间与平均服务时间 
  arr_mean = 1/lambda; 
  ser_mean = 1/mu; 
  arr_num = round(Total_time*lambda*2); 
  events = []; 
  %按负指数分布产生各顾客达到时间间隔 
  events(1,:) = exprnd(arr_mean,1,arr_num); 
  %各顾客的到达时刻等于时间间隔的累积和 
  events(1,:) = cumsum(events(1,:));
  %按负指数分布产生各顾客服务时间 
  events(2,:) = exprnd(ser_mean,1,arr_num); 
  %计算仿真顾客个数，即到达时刻在仿真时间内的顾客数 
  len_sim = sum(events(1,:)<= Total_time); 
  %***************************************** 
  %计算第 1个顾客的信息 
  %***************************************** 
  %第 1个顾客进入系统后直接接受服务，无需等待 
  events(3,1) = 0; 
  %其离开时刻等于其到达时刻与服务时间之和 
  events(4,1) = events(1,1)+events(2,1); 
  %其肯定被系统接纳，此时系统内共有 
  %1个顾客，故标志位置1 
  events(5,1) = 1; 
  %其进入系统后，系统内已有成员序号为 1 
  member = [1]; 
  
  for i = 2:arr_num 
  %如果第 i个顾客的到达时间超过了仿真时间，则跳出循环 
  if events(1,i)>Total_time break;
  else number = sum(events(4,member) > events(1,i)); 
  %如果系统已满，则系统拒绝第 i个顾客，其标志位置 0 
  if number >= N+1 
  events(5,i) = 0; 
  %如果系统为空，则第 i个顾客直接接受服务 
  else 
  if number == 0 
  %其等待时间为 0
  %PROGRAMLANGUAGEPROGRAMLANGUAGE
  events(3,i) = 0; 
  %其离开时刻等于到达时刻与服务时间之和 
  events(4,i) = events(1,i)+events(2,i); 
  %其标志位置 1 
  events(5,i) = 1; 
  member = [member,i]; 
  %如果系统有顾客正在接受服务，且系统等待队列未满，则 第 i个顾客进入系统 
  
  else len_mem = length(member); 
  %其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 
  events(3,i)=events(4,member(len_mem))-events(1,i); 
  %其离开时刻等于队列中前一个顾客的离开时刻加上其服 
  %务时间 
  events(4,i)=events(4,member(len_mem))+events(2,i); 
  %标识位表示其进入系统后，系统内共有的顾客数 
  events(5,i) = number+1; 
  member = [member,i]; 
  end 
  end 
  
  end 
  end 
  %仿真结束时，进入系统的总顾客数 
  len_mem = length(member); 
  %***************************************** 
  %输出结果 
  %***************************************** 
  %绘制在仿真时间内，进入系统的所有顾客的到达时刻和离 
  %开时刻曲线图（stairs：绘制二维阶梯图） 
  stairs([0 events(1,member)],0:len_mem); 
  hold on; 
  stairs([0 events(4,member)],0:len_mem,'.-r'); 
  legend('到达时间 ','离开时间 '); 
  hold off; 
  grid on; 
  %绘制在仿真时间内，进入系统的所有顾客的停留时间和等 
  %待时间曲线图（plot：绘制二维线性图） 
  figure;
  plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); 
  legend('等待时间 ','停留时间 '); 
  grid on;
  

• 结果
  
  

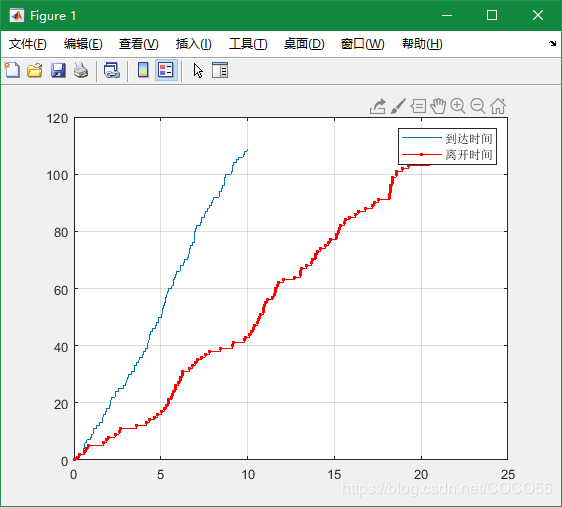
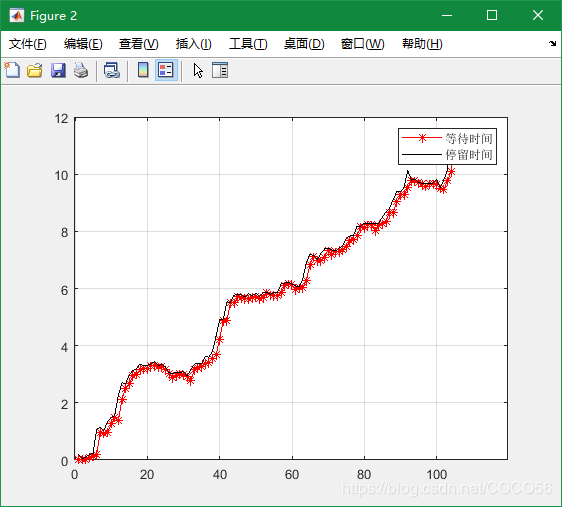
5.2.2. 测试二

提高服务率mu=12

• 源码

  clear 
  clc 
  %***************************************** 
  %初始化顾客源 
  %***************************************** 
  %总仿真时间 
  Total_time = 10; 
  %队列最大长度 
  N=10000000000; 
  %到达率与服务率 
  lambda=10, mu=12;
  %平均到达时间与平均服务时间 
  arr_mean = 1/lambda; 
  ser_mean = 1/mu; 
  arr_num = round(Total_time*lambda*2); 
  events = []; 
  %按负指数分布产生各顾客达到时间间隔 
  events(1,:) = exprnd(arr_mean,1,arr_num); 
  %各顾客的到达时刻等于时间间隔的累积和 
  events(1,:) = cumsum(events(1,:));
  %按负指数分布产生各顾客服务时间 
  events(2,:) = exprnd(ser_mean,1,arr_num); 
  %计算仿真顾客个数，即到达时刻在仿真时间内的顾客数 
  len_sim = sum(events(1,:)<= Total_time); 
  %***************************************** 
  %计算第 1个顾客的信息 
  %***************************************** 
  %第 1个顾客进入系统后直接接受服务，无需等待 
  events(3,1) = 0; 
  %其离开时刻等于其到达时刻与服务时间之和 
  events(4,1) = events(1,1)+events(2,1); 
  %其肯定被系统接纳，此时系统内共有 
  %1个顾客，故标志位置1 
  events(5,1) = 1; 
  %其进入系统后，系统内已有成员序号为 1 
  member = [1]; 
  
  for i = 2:arr_num 
  %如果第 i个顾客的到达时间超过了仿真时间，则跳出循环 
  if events(1,i)>Total_time break;
  else number = sum(events(4,member) > events(1,i)); 
  %如果系统已满，则系统拒绝第 i个顾客，其标志位置 0 
  if number >= N+1 
  events(5,i) = 0; 
  %如果系统为空，则第 i个顾客直接接受服务 
  else 
  if number == 0 
  %其等待时间为 0
  %PROGRAMLANGUAGEPROGRAMLANGUAGE
  events(3,i) = 0; 
  %其离开时刻等于到达时刻与服务时间之和 
  events(4,i) = events(1,i)+events(2,i); 
  %其标志位置 1 
  events(5,i) = 1; 
  member = [member,i]; 
  %如果系统有顾客正在接受服务，且系统等待队列未满，则 第 i个顾客进入系统 
  
  else len_mem = length(member); 
  %其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 
  events(3,i)=events(4,member(len_mem))-events(1,i); 
  %其离开时刻等于队列中前一个顾客的离开时刻加上其服 
  %务时间 
  events(4,i)=events(4,member(len_mem))+events(2,i); 
  %标识位表示其进入系统后，系统内共有的顾客数 
  events(5,i) = number+1; 
  member = [member,i]; 
  end 
  end 
  
  end 
  end 
  %仿真结束时，进入系统的总顾客数 
  len_mem = length(member); 
  %***************************************** 
  %输出结果 
  %***************************************** 
  %绘制在仿真时间内，进入系统的所有顾客的到达时刻和离 
  %开时刻曲线图（stairs：绘制二维阶梯图） 
  stairs([0 events(1,member)],0:len_mem); 
  hold on; 
  stairs([0 events(4,member)],0:len_mem,'.-r'); 
  legend('到达时间 ','离开时间 '); 
  hold off; 
  grid on; 
  %绘制在仿真时间内，进入系统的所有顾客的停留时间和等 
  %待时间曲线图（plot：绘制二维线性图） 
  figure;
  plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); 
  legend('等待时间 ','停留时间 '); 
  grid on;
  

• 结果
  
  

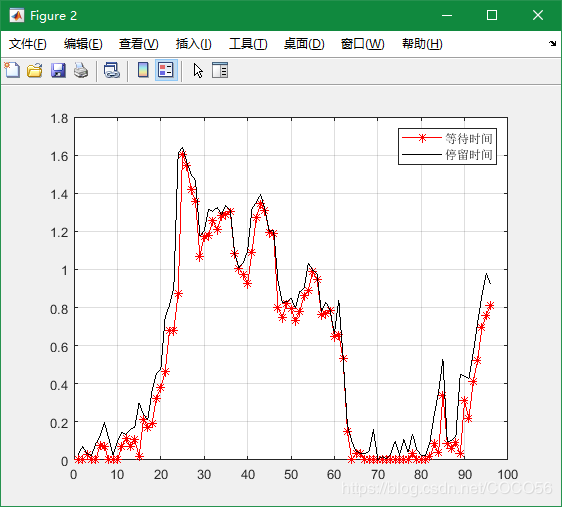
5.2.3. 测试三

增加服务台至两个，这样人数流至原来单服务台的人数减半，lambda=5

• 源码

  clear 
  clc 
  %***************************************** 
  %初始化顾客源 
  %***************************************** 
  %总仿真时间 
  Total_time = 10; 
  %队列最大长度 
  N=10000000000; 
  %到达率与服务率 
  lambda=5, mu=6;
  %平均到达时间与平均服务时间 
  arr_mean = 1/lambda; 
  ser_mean = 1/mu; 
  arr_num = round(Total_time*lambda*2); 
  events = []; 
  %按负指数分布产生各顾客达到时间间隔 
  events(1,:) = exprnd(arr_mean,1,arr_num); 
  %各顾客的到达时刻等于时间间隔的累积和 
  events(1,:) = cumsum(events(1,:));
  %按负指数分布产生各顾客服务时间 
  events(2,:) = exprnd(ser_mean,1,arr_num); 
  %计算仿真顾客个数，即到达时刻在仿真时间内的顾客数 
  len_sim = sum(events(1,:)<= Total_time); 
  %***************************************** 
  %计算第 1个顾客的信息 
  %***************************************** 
  %第 1个顾客进入系统后直接接受服务，无需等待 
  events(3,1) = 0; 
  %其离开时刻等于其到达时刻与服务时间之和 
  events(4,1) = events(1,1)+events(2,1); 
  %其肯定被系统接纳，此时系统内共有 
  %1个顾客，故标志位置1 
  events(5,1) = 1; 
  %其进入系统后，系统内已有成员序号为 1 
  member = [1]; 
  
  for i = 2:arr_num 
  %如果第 i个顾客的到达时间超过了仿真时间，则跳出循环 
  if events(1,i)>Total_time break;
  else number = sum(events(4,member) > events(1,i)); 
  %如果系统已满，则系统拒绝第 i个顾客，其标志位置 0 
  if number >= N+1 
  events(5,i) = 0; 
  %如果系统为空，则第 i个顾客直接接受服务 
  else 
  if number == 0 
  %其等待时间为 0
  %PROGRAMLANGUAGEPROGRAMLANGUAGE
  events(3,i) = 0; 
  %其离开时刻等于到达时刻与服务时间之和 
  events(4,i) = events(1,i)+events(2,i); 
  %其标志位置 1 
  events(5,i) = 1; 
  member = [member,i]; 
  %如果系统有顾客正在接受服务，且系统等待队列未满，则 第 i个顾客进入系统 
  
  else len_mem = length(member); 
  %其等待时间等于队列中前一个顾客的离开时刻减去其到 达时刻 
  events(3,i)=events(4,member(len_mem))-events(1,i); 
  %其离开时刻等于队列中前一个顾客的离开时刻加上其服 
  %务时间 
  events(4,i)=events(4,member(len_mem))+events(2,i); 
  %标识位表示其进入系统后，系统内共有的顾客数 
  events(5,i) = number+1; 
  member = [member,i]; 
  end 
  end 
  
  end 
  end 
  %仿真结束时，进入系统的总顾客数 
  len_mem = length(member); 
  %***************************************** 
  %输出结果 
  %***************************************** 
  %绘制在仿真时间内，进入系统的所有顾客的到达时刻和离 
  %开时刻曲线图（stairs：绘制二维阶梯图） 
  stairs([0 events(1,member)],0:len_mem); 
  hold on; 
  stairs([0 events(4,member)],0:len_mem,'.-r'); 
  legend('到达时间 ','离开时间 '); 
  hold off; 
  grid on; 
  %绘制在仿真时间内，进入系统的所有顾客的停留时间和等 
  %待时间曲线图（plot：绘制二维线性图） 
  figure;
  plot(1:len_mem,events(3,member),'r-*',1: len_mem,events(2,member)+events(3,member),'k-'); 
  legend('等待时间 ','停留时间 '); 
  grid on;
  

• 结果